机器学习中的数学之梯度下降法

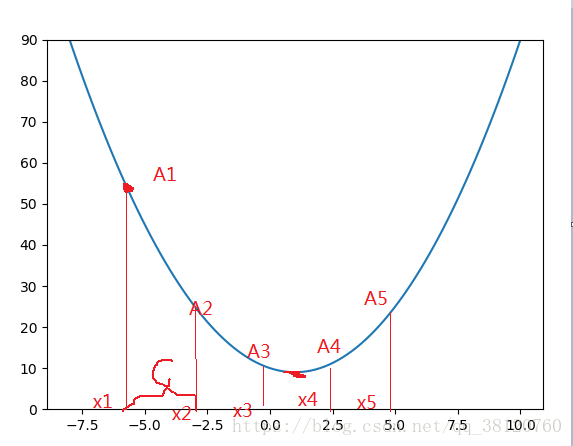
首先从一个简单的二次曲线     求极小值开始

 先任意取一个A点，对应一个横轴   但是这不是最低点。所以我们要想办法慢慢降低点的位置，让他去接近最低点。如何才能保证改变  的值得到新的    。然后  对应的函数值是小于  对应的函数值呢？第一个问题是 改变x的值让y值变小。但是我们不知道x是该增大还是变小。所以我们考虑斜率。如果当前x点的斜率为正值那么自变量与函数值是同等方向变化，即y值变小，x也变小。如果斜率为负数那么反之。

在本例中  点所在处的斜率为负，所以我们需要增大  的值才能让   变小。那么我们能不能让     其中c是一个需要我们自己给定的一个正数。如果这样的话我们每一次获取到新的 x 值都要对其对应的y值进行判断他是否小于前一个y值。如果小于就继续迭代。反之停止迭代。但是在停止时很有可能出现如下情况

显然    值小于   。    值大于  所以在 处停止迭代。但是  点并不是最低点。  所以对于此方法  常数c的值不好控制。而且几乎很难得到最优解。

所以能不能让 c 是一个变量其满足这样的一个性质。x点在越靠近最低点时，c值越小，在到达最低点的时候c为零。这样x就不会越过最低点了。而且我们不用去判断他是否到达最低点。因为 c 为零时 x 无论怎么迭代都不会改变。所以最后 x 会停留在最低点。  那么到底有没有这么一个c 呢？ 答案是有。

前面讨论了斜率的方向，接下来我们讨论一下斜率的大小。可以肯定的是在最低点附近的点的斜率一定是趋近于0的。

所以我们可以这么来定义迭代函数    其中a是一个人为给定的一个常数，用来控制下降的速率。k表示当前点的斜率。斜率越大下降为快（这里说的下降是指x的变化，不是y的变化）。下降的一般趋势是先快后慢，最后斜率为零，不再下降。本例的下降图例如下

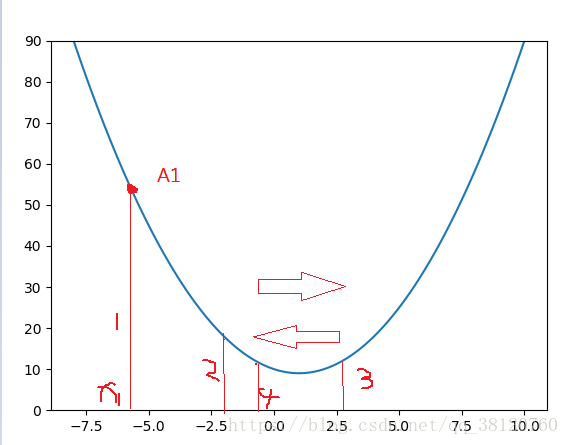
需要注意的是 a 的取值。 如果a的值太大则会发生下面的情况会直接把最低点越过。而在两点之间来回震荡。

可能会在第三个点和第四个点来回震荡。

如果a 的值过小，又会影响下降的速率。影响算法的效率。

所以需要权衡 a 的取值

下面说说对于高维多元的情况。我们只需要在每一个方向上独立下降（需要求每一个方向上的斜率，即求偏导）。每一个方向的下降速率不同，所以每一个方向收敛的时刻就不同（收敛是指斜率为0）一个方向收敛了，那么这个方向上的数值就不会在变化。当所有方向都收敛时，算法就结束了。这就是使用斜率进行迭代的好处，不用人为判断什么时候迭代结束。