$[\ NOIP\ 2009\ ]\ TG$

其他 2018-09-01 13:45:09 阅读次数: 0

\(\#A\) \(Spy\)

给出两个长度均为\(N\)相同的样例串，建立第一个串各个字符向第二个串对应位置字符的映射，并用映射转换给出的长度为\(M\)第三个串，输入保证只有大写字符。

若出现\(26\)个大写字符未建立完整，映射一些字符映射所得字符相同或同一个字符建立多个映射，则视为不合法，输出\(“failed”\)。否则，输出转换后的串。

  • \(N,M\in [1,100]\)
  • 字符串处理题，开三个数组分别记录两个样例串每个字符是否出现，以即映射。
  • 在建立映射时，判断已有映射与先前建立的映射是否相同、新建映射所得字符是否被作为映射答案出现过。
#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 30
#define M 110
#define R register
using namespace std;

bool v1[N],v2[N];
int to[N],now[M],p;

int main(){
  char c=getchar();
  while(!isupper(c)) c=getchar();
  while(isupper(c)){
    now[++now[0]]=c-'A'+1;
    v1[c-'A'+1]=1; c=getchar();
  }
  for(R int i=1;i<=26;++i) if(!v1[i]){puts("Failed");return 0;}
  while(!isupper(c)) c=getchar();
  while(isupper(c)){
    int x=now[++p];
    if(to[x]){if('A'+to[x]-1!=c){puts("Failed");return 0;}}
    else if(v2[c-'A'+1]){puts("Failed");return 0;}
    else to[x]=c-'A'+1;
    v2[c-'A'+1]=1; c=getchar();
  }
  while(!isupper(c)) c=getchar();
  while(isupper(c)){
    putchar((char)'A'+to[c-'A'+1]-1);
    c=getchar();
  }
  return 0;
}

\(\\\)

\(\#B\) \(Son\)

\(N\)组数据，每组给出四个正整数\(a_0,a_1,b_0,b_1\)，求满足\(gcd(x,a_0)=a_1,lcm[x,b_0]=b_1\)的\(x\)的个数。

  • \(N\in [1,200]\)，\(a_0,a_1,b_0,b_1\in [1,2\times 10^9]\)
  • 由 \(gcd(x,a_0)=a_1\) 得 \(gcd(\frac{x}{a_1},\frac{a_0}{a_1})=1\)

  • 由 \(lcm[x,b_0]=b_1\) 得 \(gcd(x,b_0)=\frac{x\times b_0}{b_1}\)，有 \(gcd(\frac{x}{gcd(x,b_0)},\frac{b_0}{gcd(x,b_0)})=gcd(\frac{b_1}{b_0},\frac{b_1}{x})=1\)

  • 由上知合法的\(x\)一定是\(a_1\)的倍数，一定是\(b_1\)的因数，所以得到一个做法，试除法\(\Theta(\sqrt b_1)\)求\(b_1\)因数，判断是否为\(a_1\)因数，再进一步判断推出的两个条件是否成立，总复杂度\(\Theta(N\sqrt {2\times10^9}log(2\times10^9))\approx\Theta(8\times 10^7)\)

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define R register
#define gc getchar
using namespace std;

inline int rd(){
    int x=0; char c=gc();
    while(!isdigit(c)) c=gc();
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
    return x;
}

inline int gcd(int x,int y){return y?gcd(y,x%y):x;}

inline void work(){
    int a0=rd(),a1=rd(),b0=rd(),b1=rd();
  int ans=0,lim=sqrt(b1); a0/=a1; b0=b1/b0;
    for(R int x=1;x<=lim;++x)
        if(!(b1%x)){
            if(!(x%a1)&&gcd(x/a1,a0)==1&&gcd(b1/x,b0)==1)++ans;
            if(x*x==b1)continue;
            int k=b1/x;
            if(!(k%a1)&&gcd(k/a1,a0)==1&&gcd(b1/k,b0)==1)++ans;
        }
    printf("%d\n",ans);
}

int main(){
    int t=rd();
    while(t--)work();
    return 0;
}

\(\\\)

\(\#C\) \(Trade\)

给出一个\(N\)个节点\(M\)条边的图，边有向边和无向边两种，每个点有点权\(V_i\)。

求出一条从\(1\)号节点到\(N\)号节点的路径，使得在路径上有两个点\(u,v\)，保证\(u\)在\(v\)之前出现，且\(V_v-V_u\)的值最大，输出该值即可。

  • \(N\in [1,10^5]\)，\(M\in [1,5\times 10^5]\)，\(V_i\in [1,100]\)

最短路：

  • 考虑无向边拆成两条有向边，跑一个以\(1\)为源的单源最短路，统计从\(1\)号节点到该节点路径上最小点权，更新变成\(dismin[v]=min(dismin[u],V_v)\)，该值代表若选择从\(1\)号节点到这个节点的路径，选这个点作为\(u\)点。

  • 然后就是统计从这个点到\(n\)号节点路径上最大点权，代表选这个点作为\(u\)点，统计方式可以考虑建一个反图，跑以\(n\)为源的单元最短路，统计从\(n\)号节点到该节点路径上的最大点权，也就是原图中从该节点到\(n\)号节点的最大点权，更新变成\(dismax[v]=max(dismax[u],V_v)\)。

  • 对每个点用\(dismax[i]-dismin[i]\)更新答案即可。

  • 注意到题目所给图较稀疏，\(SPFA\)运行效率比堆优化\(Dijkstra\)实测更优秀一些。

    \(SPFA\)版本

    #include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 100010
#define M 1000010
#define R register
#define gc getchar
using namespace std;

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

int hd1[N],hd2[N],tot1,tot2;
struct edge{int to,nxt;}e1[M],e2[M];
inline void add1(int u,int v){
  e1[++tot1].to=v; e1[tot1].nxt=hd1[u]; hd1[u]=tot1;
}
inline void add2(int u,int v){
  e2[++tot2].to=v; e2[tot2].nxt=hd2[u]; hd2[u]=tot2;
}

bool vis1[N],vis2[N];
int n,m,ans,mn[N],mx[N],val[N];
queue<int> q1,q2;

inline void SPFA1(){
    memset(mn,0x3f,sizeof(mn));
    mn[1]=val[1]; q1.push(1);
    while(!q1.empty()){
      int u=q1.front(); q1.pop(); vis1[u]=0;
      for(R int i=hd1[u],v;i;i=e1[i].nxt)
        if(mn[v=e1[i].to]>min(val[v],mn[u])){
            mn[v]=min(val[v],mn[u]);
            if(!vis1[v]) q1.push(v); vis1[v]=1;
        }
    }
}

inline void SPFA2(){
    mx[n]=val[n]; q2.push(n);
    while(!q2.empty()){
      int u=q2.front(); q2.pop(); vis2[u]=0;
      for(R int i=hd2[u],v;i;i=e2[i].nxt)
        if(mx[v=e2[i].to]<max(val[v],mx[u])){
            mx[v]=max(val[v],mx[u]);
            if(!vis2[v]) q2.push(v); vis2[v]=1;
        }
    }
}

int main(){
  n=rd(); m=rd();
  for(R int i=1;i<=n;++i) val[i]=rd();
  for(R int i=1,u,v,w;i<=m;++i){
    u=rd(); v=rd(); w=rd();
    add1(u,v); add2(v,u);
    if(w==2){add1(v,u); add2(u,v);}
  }
  SPFA1(); SPFA2();
  for(R int i=1;i<=n;++i) ans=max(ans,mx[i]-mn[i]);
  printf("%d\n",ans);
  return 0;
}

    \(Dijkstra\)版本

    #include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 100010
#define M 1000010
#define R register
#define gc getchar
using namespace std;

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

int hd1[N],hd2[N],tot1,tot2;
struct edge{int to,nxt;}e1[M],e2[M];
inline void add1(int u,int v){
  e1[++tot1].to=v; e1[tot1].nxt=hd1[u]; hd1[u]=tot1;
}
inline void add2(int u,int v){
  e2[++tot2].to=v; e2[tot2].nxt=hd2[u]; hd2[u]=tot2;
}

bool vis1[N],vis2[N];
int n,m,ans,mn[N],mx[N],val[N];
priority_queue<pair<int,int> > q1,q2;

inline void dij1(){
    memset(mn,0x3f,sizeof(mn));
    mn[1]=val[1];
    q1.push(make_pair(-val[1],1));
    while(!q1.empty()){
      int u=q1.top().second; q1.pop();
      if(vis1[u]) continue; vis1[u]=1;
      for(R int i=hd1[u],v;i;i=e1[i].nxt)
        if(mn[v=e1[i].to]>min(val[v],mn[u])){
          mn[v]=min(val[v],mn[u]);
          q1.push(make_pair(-mn[v],v));
        }
    }
}

inline void dij2(){
    mx[n]=val[n];
    q2.push(make_pair(val[n],n));
    while(!q2.empty()){
      int u=q2.top().second; q2.pop();
      if(vis2[u]) continue; vis2[u]=1;
      for(R int i=hd2[u],v;i;i=e2[i].nxt)
        if(mx[v=e2[i].to]<max(val[v],mx[u])){
          mx[v]=max(val[v],mx[u]);
          q2.push(make_pair(mx[v],v));
        }
    }
}

int main(){
  n=rd(); m=rd();
  for(R int i=1;i<=n;++i) val[i]=rd();
  for(R int i=1,u,v,w;i<=m;++i){
    u=rd(); v=rd(); w=rd();
    add1(u,v); add2(v,u);
    if(w==2){add1(v,u); add2(u,v);}
  }
  dij1(); dij2();
  for(R int i=1;i<=n;++i) ans=max(ans,mx[i]-mn[i]);
  printf("%d\n",ans);
  return 0;
}

\(Tarjan+DFS\)：

  • 同样无向边拆成两条有向边，\(Tarjan\)找\(SCC\)缩点，记录每个\(SCC\)内最大点权和最小点权，因为\(SCC\)内可以一直转圈，所以最大最小点权在这个\(SCC\)内一定可以得到。建新图时注意，若为节省空间使用同一个邻接表，需清空\(head\)数组。

  • 考虑到缩点后一些路径不会经过\(1\)号或\(N\)号节点，所以不能拓扑排序，只能记忆化搜索。记\(f_i\)表示\(i\)号结点到\(N\)号节点的路径上的最大值。为了防止路径不可由\(1\)号节点引出，可以选择只从\(1\)号节点\(DFS\)。防止路径不可到达\(N\)号节点，选择只有到达\(N\)号节点所属\(SCC\)时才更新\(f\)数组，其余时由其他可达点更新当前点。

  • 若\(DFS\)所有可达点之后\(f_i\)不是默认值则证明其可达\(N\)号节点，则可进一步用\(sccmax_{i}\)更新\(f_i\)，并进一步用\(f_i-sccmin_i\)更新答案，代表在这个\(SCC\)买入，在从此开始后续\(SCC\)中最大点卖出。

    #include<cmath>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 100010
#define M 500010
#define R register
#define gc getchar
#define top stk[0]
using namespace std;

bool vis[N];
int n,m,tot,ans,hd[N],val[N],f[N];
int num,cnt,low[N],dfn[N],bl[N],stk[N],mn[N],mx[N];
struct adjlist{int to,nxt;}e[M<<1];
struct Edge{int x,y;}edge[M<<1];

inline void add(int u,int v){
  e[++tot].to=v; e[tot].nxt=hd[u]; hd[u]=tot;
}

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

inline void tarjan(int u){
  stk[++top]=u; vis[u]=1;
  dfn[u]=low[u]=++cnt;
  for(R int i=hd[u],v;i;i=e[i].nxt)
    if(!dfn[v=e[i].to]){
      tarjan(v); low[u]=min(low[u],low[v]);
    }
    else if(vis[v]) low[u]=min(low[u],dfn[v]);
  if(dfn[u]==low[u]){
    ++num;
    do{
      bl[stk[top]]=num;
      vis[stk[top]]=0;
      mn[num]=min(mn[num],val[stk[top]]);
      mx[num]=max(mx[num],val[stk[top--]]);
    }while(stk[top+1]!=u);
  }
}

inline bool cmp(Edge a,Edge b){return (a.x==b.x)?(a.y<b.y):a.x<b.x;}

inline void dfs(int u){
  vis[u]=1;
  if(u==bl[n]) f[u]=max(f[u],mx[u]);
  for(R int i=hd[u],v;i;i=e[i].nxt){
    if(!vis[v=e[i].to]) dfs(v);
    f[u]=max(f[u],f[v]);
  }
  if(f[u]) f[u]=max(f[u],mx[u]);
  ans=max(ans,f[u]-mn[u]);
}

int main(){
  n=rd(); m=rd();
  for(R int i=1;i<=n;++i) val[i]=rd();
  for(R int i=1,u,v;i<=m;++i){
    u=rd(); v=rd();
    add(u,v); if(rd()==2) add(v,u);
  }
  memset(mn,0x3f,sizeof(mn)); tarjan(1);
  int tmp=0; tot=0;
  for(R int i=1;i<=n;++i)
    for(R int j=hd[i],v;j;j=e[j].nxt)
      if(bl[i]!=bl[v=e[j].to]){edge[++tmp].x=bl[i];edge[tmp].y=bl[v];}
  sort(edge+1,edge+1+tmp,cmp);
  memset(hd,0,sizeof(hd));
  for(R int i=1;i<=tmp;++i)
    if(edge[i].x!=edge[i-1].x||edge[i].y!=edge[i-1].y) add(edge[i].x,edge[i].y);
  dfs(bl[1]);
  printf("%d\n",ans);
  return 0;
}

\(\\\)

\(\#D\) \(Sudoku\)

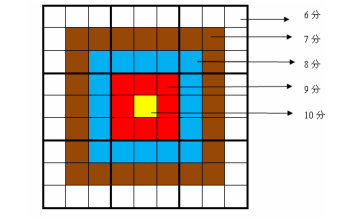
给出一个未完成的九宫数独，并定义每一个位置的权值：

求保证填数合法的前提下，完成这个数独所能得到的权值和最大是多少。

  • 数据保证已填入的数不少于\(24\)个。

\(DFS:\)

  • 扫描一遍整个数独，记录下所有待填数的位置，同时记录该位置可能填入的数字，按顺序搜索到合法解即可。
  • 一个看起来正确的优化是按照可能填入的数字个数排序，或按照所在行\(/\)列\(/\)宫剩余位置个数排序，这样在搜索的时候能够使搜索树上的较低层节点数尽可能地优秀。
  • 实测不开\(\text O 2\)最好的状态下只会超时\(1\)个点。

  • 基本的数独转精确覆盖问题及\(Dancing\ Links\ X\)解法可以参考：\(Dancing\ Links\ X\)

  • 与基本的数独做法相同，但在找到答案之后不直接\(return\)，而要搜完所有的状态。

  • 在计算过程中\(dance\)函数可以传一个当前权值和的参数，因为每一行只代表一个位置的一个方案，所以具体的实现过程可以对每一行先绑定权值，然后选择行的时候答案就可以直接累加了。

#include<cmath>
#include<vector>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 750
#define M 350
#define S 247500
#define R register
#define gc getchar
using namespace std;

inline int rd(){
  int x=0; bool f=0; char c=gc();
  while(!isdigit(c)){if(c=='-')f=1;c=gc();}
  while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}
  return f?-x:x;
}

inline int calc(int x,int y,int k){return x*81+y*9+k+1;}

inline void restore(int ans,int &x,int &y,int &k){
  k=(--ans)%9; ans/=9; y=ans%9; x=(ans/9)%9;
}

vector<int> res;
int t,n,m,maxr=729,maxc=324,num[10][10];
const int score[9][9]={
  {6,6,6,6,6,6,6,6,6},
  {6,7,7,7,7,7,7,7,6},
  {6,7,8,8,8,8,8,7,6},
  {6,7,8,9,9,9,8,7,6},
  {6,7,8,9,10,9,8,7,6},
  {6,7,8,9,9,9,8,7,6},
  {6,7,8,8,8,8,8,7,6},
  {6,7,7,7,7,7,7,7,6},
  {6,6,6,6,6,6,6,6,6}
};


struct dlx{

  int n,m,tot,ans=-1,s[M],h[N];

    int u[S],d[S],l[S],r[S],row[S],col[S];

  inline void reset(int _n,int _m){
    n=_n; m=_m;
    for(R int i=0;i<=m;++i){l[i]=i-1; r[i]=i+1; u[i]=d[i]=i;}
    l[0]=m; r[m]=0; tot=m;
    memset(s,0,sizeof(s));
    memset(h,-1,sizeof(h));
  }

  inline void insert(int x,int y,int k){
    row[++tot]=k; col[tot]=y; ++s[y];
    u[tot]=u[y]; d[tot]=y;
    d[u[tot]]=tot; u[d[tot]]=tot;
    if(h[x]==-1){h[x]=tot; l[tot]=tot; r[tot]=tot;}
    else{
      l[tot]=l[h[x]]; r[tot]=h[x];
      r[l[tot]]=tot; l[r[tot]]=tot;
    }
  }

  inline void remove(int y){
    r[l[y]]=r[y]; l[r[y]]=l[y];
    for(R int i=d[y];i!=y;i=d[i])
      for(R int j=r[i];j!=i;j=r[j]){
        u[d[j]]=u[j]; d[u[j]]=d[j]; --s[col[j]];
      }
  }

  inline void restore(int y){
    for(R int i=d[y];i!=y;i=d[i])
      for(R int j=r[i];j!=i;j=r[j]){
        u[d[j]]=j; d[u[j]]=j; ++s[col[j]];
      }
    r[l[y]]=y; l[r[y]]=y;
  }

  inline void dance(int sum){
    if(r[0]==0){ans=max(ans,sum);return;}
    int y=r[0];
    for(R int i=r[0];i!=0;i=r[i]) if(s[i]<s[y]) y=i;
    remove(y);
    for(R int i=d[y];i!=y;i=d[i]){
      for(R int j=r[i];j!=i;j=r[j]) remove(col[j]);
      dance(sum+row[i]);
      for(R int j=l[i];j!=i;j=l[j]) restore(col[j]);
    }
    restore(y); return;
  }

}dlx;

int main(){
  dlx.reset(maxr,maxc);
  for(R int i=0;i<=8;++i)
    for(R int j=0;j<=8;++j) num[i][j]=rd();
  for(R int i=0;i<=8;++i)
    for(R int j=0;j<=8;++j)
      for(R int k=0;k<=8;++k)
        if(num[i][j]==0||num[i][j]==k+1){
          int x=calc(i,j,k);
          dlx.insert(x,calc(0,i,j),score[i][j]*(k+1));
          dlx.insert(x,calc(1,i,k),score[i][j]*(k+1));
          dlx.insert(x,calc(2,j,k),score[i][j]*(k+1));
          dlx.insert(x,calc(3,(i/3)*3+j/3,k),score[i][j]*(k+1));
        }
  dlx.dance(0);
  printf("%d\n",dlx.ans);
  return 0;
}

猜你喜欢

转载自www.cnblogs.com/SGCollin/p/9550634.html
今日推荐
开源日报 | Chrome内置Gemini的意义不在于Gemini；中国AI追随之路的五大误区；ECharts创始人“下海”养鱼；谷歌I/O开发者大会什么都有，只是没有惊喜
微软回应中国区AI团队“打包赴美”传闻
基于大语言模型的开源知识库问答系统 MaxKB GitHub Star 数量突破 5,000 个！
美国拟限制 AI 大模型出口中国和俄罗斯
苹果将与 OpenAI 达成协议，将 ChatGPT 应用于 iPhone
openKylin 社区生态委员会第六次会议圆满召开
阿里云正式发布通义千问 2.5
Python 3.13 发布首个 Beta：实验性自由线程模式和 JIT、改进交互式解释器
Stack Overflow 拿我的代码去训练 AI 大模型，还封了我的账号
Pop!_OS 的 COSMIC 桌面完成 App Store 上架工作
《2024 年一季度互联网投融资运行情况》研究报告
报告：Django 仍然是 74% 开发者的首选
周排行
返回指定时间格式
fopen函数中的mode参数
Java 单例模式探讨
Flex remoteobject工作原理探讨
寻找mplayer的便捷安装方法
30天了解30种技术系列---(26)MySQL自动化运维工具Inception
关于Jboss/Tomcat/Jetty的JNDI定义123
程序减肥，strip，eu-strip 及其符号表
AsyncTask、View.post(Runnable)、ViewTreeObserver三种方式总结frame animation自动启动
Json和Bean的互相转换
每日归档
更多
2024-05-15(24)
2024-05-14(0)
2024-05-13(18)
2024-05-12(0)
2024-05-11(38)
2024-05-10(38)
2024-05-09(35)
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022