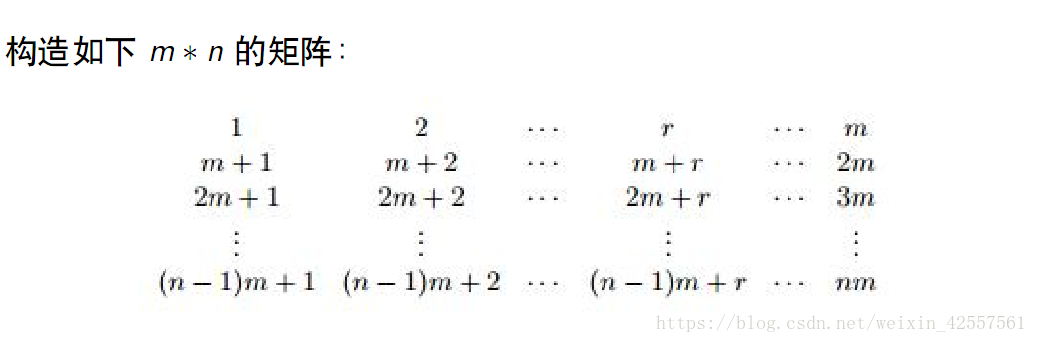版权声明:虽然我只是个小蒟蒻但转载也请注明出处哦 https://blog.csdn.net/weixin_42557561/article/details/82288785
【写在前面】
一个数若既与 m 互质又与 n 互质,那么他便和 m*n 互质
完全剩余系:一个整数的集合,对 m 取模后,余数遍历了 0; 1; 2; 3; ……m
欧拉函数:phi(n)-->不超过n且与n互质的整数的个数
特别的:phi(1)=1
现在我们需要证明phi(m*n ) = phi (m )*phi(n) 【m,n互质】
这个矩阵里列举了从1到m*n的所有数,很容易发现第一行里有phi(m)个与 m 互质的数,而一个数 r 若与 m 互质,则 k * m + r也与m互质,这是显而易见的
然后看任意一列,可以得出结论任意一列都是 n 的完全剩余系,(也就是说没有两个数他们对 n 取模后相等),那么任意一列都有phi(n)个与n互质的数,那么phi(n)*phi(m)便等于 phi(n*m)
所以为什么 任意一列都是 n 的完全剩余系呢?
首先我们假设有两个数对n取余后相等:k1*m+b = k2*m+b (mod n),那么我们可以改写为k1*m+b = t1*n+r ; k2*m+b= t2*n+r,两两相减则: (k1-k2)m = (t1-t2)n,又因为m和n互质,所以m不能提供n的因数,那么(k1-k2)就必然是n的倍数了,然后又因为k1和k2都是在0~n-1这个范围里的,所以任意两个相减都不会产生n的倍数,那么假设不成立,没有两个数对n取余后相等,证毕