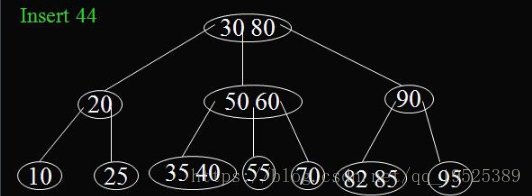
B-tree
B-tree是一种适用于外查找的树,它是一种平衡的多叉树,称为B-树(或B树、B_树)。
一棵m阶B树是一棵平衡的m路搜索树。它或者是空树,或者是满足下列性质的树:
1、根结点至少有两个子女;
2、每个非根节点所包含的关键字个数 j 满足:┌m/2┐ - 1 <= j <= m - 1;(┌m/2┐为大于m/2的最小整数)
3、除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足:┌m/2┐ <= k <= m ;
4、所有的叶子结点都位于同一层。
在B-树中,每个结点中关键字从小到大排列,并且当该结点的孩子是非叶子结点时,该k-1个关键字正好是k个孩子包含的关键字的值域的分划。
因为叶子结点不包含关键字,所以可以把叶子结点看成在树里实际上并不存在外部结点,指向这些外部结点的指针为空,叶子结点的数目正好等于树中所包含的关键字总个数加1。
B-树中的一个包含n个关键字,n+1个指针的结点的一般形式为: (n,P0,K1,P1,K2,P2,…,Kn,Pn)
其中,Ki为关键字,K1<K2<…<Kn, Pi 是指向包括Ki到Ki+1之间的关键字的子树的指针。
查找:
首先把根结点取来,在根结点所包含的关键字K1,…,Kn查找给定的关键字(可用顺序查找或二分查找法),若找到等于给定值的关键字,则查找成功;否则,一定可以确定要查找的关键字在Ki与Ki+1之间,Pi为指向子树根节点的指针,此时取指针Pi所指的结点继续查找,直至找到,或指针Pi为空时查找失败。
插入:
当在叶子结点处于第L+1层的B树中插入关键字时,被插入的关键字总是进入第L层的结点。
若在一个包含j<m-1个关键字的结点中插入一个新的关键字,则把新的关键字直接插入该结点即可;但若把一个新的关键字插入到包含m-1(m为B-树的阶)个关键字的结点中,则将引起结点的分裂。在这种情况下,要把这个结点分裂为两个,并把中间的一个关键字(中间的关键字满足:左边的小于该关键字;右边的大于该关键字;故正好可以作为双亲)拿出来插到该结点的双亲结点中去,双亲结点也可能是满的,就需要再分裂、再往上插,从而可能导致B-树可能朝着根的方向生长。
删除:
当从B-树中删除一个关键字Ki时,总的分为以下两种情况:
(一)如果该关键字所在的结点不是最下层的非叶子结点,
①首先要将其转化成在叶子节点上,再按下面(二)进行删除操作
② 转化过程:
1)找到相邻关键字:即需删除关键字的左子树中的最大关键字或右子树中的最小关键字(可以先到左子树,再一直按右指针往下找;或在右子树中,按左指针往下找)
2)用相邻关键字来覆盖需删除的非叶子节点关键字,在删除原相邻关键字。
(二)如果该关键字所在的结点正好是最下层的非叶子结点,这种情况下,会有以下两种可能:
① 若该关键字Ki所在结点中的关键字个数不小于┌m/2┐,则可以直接从该结点中删除该关键字和相应指针即可。
② 若该关键字Ki所在结点中的关键字个数小于┌m/2┐,则直接从结点中删除关键字会导致此结点中所含关键字个数小于┌m/2┐-1 。这种情况下,需考察该结点在B树中的左或右兄弟结点,先左后右地从兄弟结点中移若干个关键字到该结点中来(这也涉及它们的双亲结点中的一个关键字要作相应变化),使两个结点中所含关键字个数基本相同;但如果其兄弟结点的关键字个数也很少,刚好等于┌m/2┐-1 ,这种移动则不能进行,这种情形下,需要先左后右地把删除了关键字Ki的结点、它的兄弟结点及它们双亲结点中的一个关键字合并为一个结点。
B+树
B+ 树是一种树数据结构,是一个n叉排序树。一棵B+树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点,也可能是一个包含两个或两个以上孩子节点的节点。
定义:
B+树是应文件系统所需而出的一种B树的变型树。一棵m阶的B+树和m阶的B-树的差异在于:
1.有n棵子树的结点中含有n个关键字,每个关键字不保存数据,只用来索引,所有数据都保存在叶子节点。
2.所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
3.所有的非终端结点可以看成是索引部分,结点中仅含其子树(根结点)中的最大关键字。
查找:
对B+树可以进行两种查找运算:
1.从最小关键字起顺序查找;
2.从根结点开始,进行随机查找。
在查找时,若非终端结点上的关键值等于给定值,并不终止,而是继续向下直到叶子结点。因此,在B+树中,不管查找成功与否,每次查找都是走了一条从根到叶子结点的路径。其余同B-树的查找类似。
通常在B+树上有两个头指针,一个指向根结点,一个指向关键字最小的叶子结点。
插入:
m阶B树的插入操作在叶子结点上进行,假设要插入关键值a,找到叶子结点后插入a,做如下算法判别:
①如果当前结点是根结点并且插入后结点关键字数目小于等于m,则算法结束;
②如果当前结点是非根结点并且插入后结点关键字数目小于等于m,则判断若a是新索引值时转步骤④后结束,若a不是新索引值则直接结束;
③如果插入后关键字数目大于m(阶数),则结点先分裂成两个结点X和Y,并且他们各自所含的关键字个数分别为:u=大于(m+1)/2的最小整数,v=小于(m+1)/2的最大整数;
由于索引值位于结点的最左端或者最右端,不妨假设索引值位于结点最右端,有如下操作:
如果当前分裂成的X和Y结点原来所属的结点是根结点,则从X和Y中取出索引的关键字,将这两个关键字组成新的根结点,并且这个根结点指向X和Y,算法结束;
如果当前分裂成的X和Y结点原来所属的结点是非根结点,依据假设条件判断,如果a成为Y的新索引值,则转步骤④得到Y的双亲结点P,如果a不是Y结点的新索引值,则求出X和Y结点的双亲结点P;然后提取X结点中的新索引值a’,在P中插入关键字a’,从P开始,继续进行插入算法;
④提取结点原来的索引值b,自顶向下,先判断根是否含有b,是则需要先将b替换为a,然后从根结点开始,记录结点地址P,判断P的孩子是否含有索引值b而不含有索引值a,是则先将孩子结点中的b替换为a,然后将P的孩子的地址赋值给P,继续搜索,直到发现P的孩子中已经含有a值时,停止搜索,返回地址P。
删除:
如果叶子结点中没有相应的key,则删除失败。否则执行下面的步骤
1)删除叶子结点中对应的key。删除后若结点的key的个数大于等于Math.ceil(m/2) – 1,删除操作结束,否则执行第2步。
2)若兄弟结点key有富余(大于Math.ceil(m/2) – 1),向兄弟结点借一个记录,同时用借到的key替换父结(指当前结点和兄弟结点共同的父结点)点中的key,删除结束。否则执行第3步。
3)若兄弟结点中没有富余的key,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的key(父结点中的这个key两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第4步(第4步以后的操作和B树就完全一样了,主要是为了更新索引结点)。
4)若索引结点的key的个数大于等于Math.ceil(m/2) – 1,则删除操作结束。否则执行第5步
下面是一颗5阶B树的删除过程,5阶B数的结点最少2个key,最多4个key。
a)初始状态
b)删除22,删除后结果如下图
删除后叶子结点中key的个数大于等于2,删除结束
c)删除15,删除后的结果如下图所示
删除后当前结点只有一个key,不满足条件,而兄弟结点有三个key,可以从兄弟结点借一个关键字为9的记录,同时更新将父结点中的关键字由10也变为9,删除结束。
d)删除7,删除后的结果如下图所示
当前结点关键字个数小于2,(左)兄弟结点中的也没有富余的关键字(当前结点还有个右兄弟,不过选择任意一个进行分析就可以了,这里我们选择了左边的),所以当前结点和兄弟结点合并,并删除父结点中的key,当前结点指向父结点。
此时当前结点的关键字个数小于2,兄弟结点的关键字也没有富余,所以父结点中的关键字下移,和两个孩子结点合并,结果如下图所示。
5)若兄弟结点有富余,父结点key下移,兄弟结点key上移,删除结束。否则执行第6步
6)当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点,重复第4步。
注意,通过B+树的删除操作后,索引结点中存在的key,不一定在叶子结点中存在对应的记录。
一棵m阶的B+树和m阶的B树的异同点在于:
-
所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。(而B 树的叶子节点并没有包括全部需要查找的信息)
-
所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。(而B 树的非终节点也包含需要查找的有效信息)
B+树比B 树更适合实际应用中操作系统的文件索引和数据库索引?
-
B+树的磁盘读写代价更低
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
举个例子,假设磁盘中的一个盘块容纳16bytes,而一个关键字2bytes,一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘块。而B+树内部结点只需要1个盘块。当需要把内部结点读入内存中的时候,B 树就比B+树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。
-
B+树的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
数据库索引采用B+树的主要原因是 B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题,B+树应运而生。B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作(或者说效率太低)
关系数据库中,索引大多采用B/B+树来作为存储结构,而全文搜索引擎的索引则主要采用hash表的存储结构,为什么?
hash结构的特点:检索效率非常高,索引的检索可以一次到位,O(1)。B树需要从根节点到枝节点,最后才能到叶节点进行多次I/O操作,所以hash的效率远远高于B树的效率。
那么为什么数据库索引还是用B树结构呢?
1、hash索引仅满足“=”、“IN”和“<=>”查询,不能使用范围查询
因为hash索引比较的是经常hash运算之后的hash值,因此只能进行等值的过滤,不能基于范围的查找,因为经过hash算法处理后的hash值的大小关系,并不能保证与处理前的hash大小关系对应。
2、hash索引无法被用来进行数据的排序操作
由于hash索引中存放的都是经过hash计算之后的值,而hash值的大小关系不一定与hash计算之前的值一样,所以数据库无法利用hash索引中的值进行排序操作。
3、对于组合索引,Hash 索引在计算 Hash 值的时候是组合索引键合并后再一起计算 Hash 值,而不是单独计算 Hash 值,所以通过组合索引的前面一个或几个索引键进行查询的时候,Hash 索引也无法被利用。
4、Hash 索引遇到大量Hash值相等的情况后性能并不一定就会比B-Tree索引高。
对于选择性比较低的索引键,如果创建 Hash 索引,那么将会存在大量记录指针信息存于同一个 Hash 值相关联。这样要定位某一条记录时就会非常麻烦,会浪费多次表数据的访问,而造成整体性能低下。
(因此:键值重复率低的适合用B树索引)
b-tree完全基于key的比较,和二叉树相同的道理,相当于建个排序后的数据集,使用二分法查找算法,实际上也非常快,而且受数据量增长影响非常小