机器学习：支持向量机(SVM)与Python实现第(一)篇

版权声明：本文为博主原创文章，未经许可，请勿转载 https://blog.csdn.net/liweibin1994/article/details/77504210

前言

最近看了Andrew Ng的机器学习视频中的支持向量机，视频的内容比较浅显，没有深入解释支持向量机中的数学原理。但是对于一个比较执着于知道为什么的人，笔者还是去网上查找了有关支持向量机原理以及实现的相关资料。在查找的过程中，笔者发现支持向量机的内容还是蛮多的，于是笔者根据自己的理解，并且参考了一些相关资料，最终写下了支持向量机的四篇博客。
机器学习：支持向量机(SVM)与Python实现第(一)篇——此篇主要介绍了分类间隔，引入SVM。
机器学习：支持向量机(SVM)与Python实现第(二)篇——此篇主要介绍了使用拉格朗日乘子来简化SVM问题的优化。
机器学习：支持向量机(SVM)与Python实现第(三)篇——此篇主要介绍非线性分类(核函数)以及松弛变量。
机器学习：支持向量机(SVM)与Python实现第(四)篇——此篇主要介绍SMO算法并用python实现了简单的SVM分类器。

引子

一开始听到支持向量机这个名词，我还以为是某种机器呢。其实它确实可以算是一个机器，只不过它是算法层面的机器，用来给数据分类的。

首先我们来回顾一下逻辑回归(logistic regression)。在逻辑回归中，我们的假设函数(hypothesis function)为：

$$\ \ h_{\theta}(x) = g(\theta^{T}x)\ \ $$

对于一个输入$x^{(i)}$, 如果$h_{\theta}(x^{(i)})\geq 0.5$ 我们将预测结果为“1”，等价于$\theta^{T}x\geq 0$ 。对于一个正例(即y=1)来说，$\theta^{T}x$ 的值越大，$h_{\theta}(x)$ 的值就会越接近于1，也就是说我们有更大的确信度(confidence)来说明对于这个输入x，它的标签(类别)是属于1。对于反例也是同样的道理。

因此，我们其实希望得到的一组$\theta$，对于每个输入x来说，当y=1时，$\theta^{T}x$ 的值都能够尽可能的大于0($\theta^{T}x\gg 0$),或者当y=0时，$\theta^{T}x$ 的值尽可能小于0($\theta^{T}x\ll 0$ )。这样我们就会有更大的确信度了。

现在，让我们抛开逻辑回归，来考虑一个线性分类的问题。

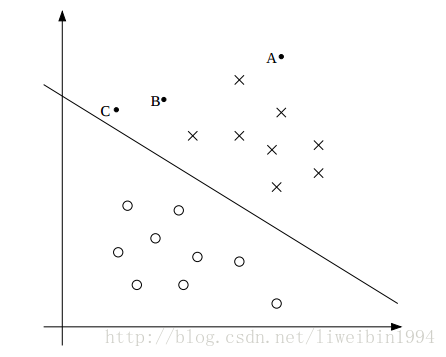
如上图所示，其中打叉的表示正样本，圆圈表示负样本。直线就是决策边界(它的方程表示为$\theta^{T}x=0$),或者叫做分离超平面(separating hyperplane)。
对于图中的A点来说，它距离决策边界很远。如果要我们预测一下A点对应的y值，我们应该会很确定地说y=1。反过来，对于C点来说，它距离决策边界很近。虽然它也是在决策边界的上方，但是只要决策边界有稍微的改变，它就可能变成在决策边界的下方。所以相比较而言，我们对于预测A点的自信要比预测C点要高。

所以，对于一组训练集，我们希望所有的样本都距离决策边界很远，这样我们确信度就高。而要使样本距离决策边界都很远，我们只需要保证距离决策边界最近的点的距离都很大，那么其它的点的距离肯定就更大了。怎么距离又是说大又是说小呢？理解如下：

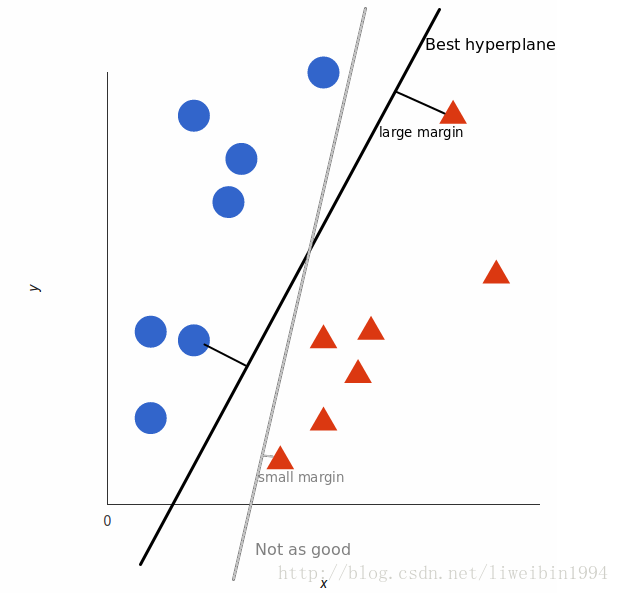
分类超平面可以有多个，上图中的灰色线已经将两个类别分开了，但是为什么说它not as good呢？因为距离灰色线最近的点(最下面的红色三角形)的边距很小(small margin)。相反，对于黑色线，距离它最近的点(最上面的红色的三角形)的边距很大(large margin)，这个大是指比灰色线的那个margin要大。我们要找的就是看看哪个超平面的最近点的边距最大。

那么我们怎么来刻画这个距离(margin)呢？

首先为了方便，我们分类的标签记为$y\in {\{-1,1\}}$ 而不是逻辑回归中的$\{0,1\}$，这只是一种区分的方式，只是为了方便。另外，以前我们用的是参数向量$\theta$，现在将$\theta$ 分成w和b，其实就是$b=\theta_0，x_0=1$。所以分类器写为：

$$h_{w,b}(x)=g(w^{T}x+b)$$ 其中， $g(z)=1\ if \ z \geq 0,\ g(z)=-1\ otherwise$，注意这里不像逻辑回归那样先算出概率，再判断y是否等于1。这里直接预测y是否为1。

扫描二维码关注公众号，回复： 3313367 查看本文章

---

函数间距(functional margins)与几何间距(geometric margins)

d
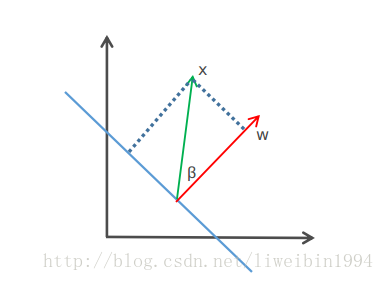
如上图，点x到蓝色线的距离$L = \beta \left \| x \right \|$，也就是$\frac{<x,w>}{\left \| w \right \|}$。这是高中的几何知识啦。

现在让我们来定义一下函数间距。对于一个训练样本$(x^{(i)},y^{(i)})$，我们定义相应的函数间距为：

$$\hat{\gamma}^{(i)}=y^{(i)}(w^{T}x^{(i)}+b)=y^{(i)}g(x^{(i)})$$ 注意前面乘上类别 y 之后可以保证这个 margin 的非负性(因为g(x)<0对应y=-1的那些点)。

所以，如果$y^{(i)}=1$，为了让函数间距比较大(预测的确信度就大)，我们需要$w^{T}x^{(i)}+b$ 是一个大的正数。反过来，如果$y^{(i)}=-1$，为了让函数间距比较大(预测的确信度就大)，我们需要$w^{T}x^{(i)}+b$ 是一个大的负数。
好了，有了函数间距的定义，我们接下来就是要找所有点中间距最小的点了。对于给定的数据集$S = {(x^{(i)},y^{(i)});i=1,...,m}$，我们定义$\hat{\gamma}$ 是数据集中函数间距最小的，即：

$$\hat{\gamma} = \underset{i=1,...,m}{min}\hat{\gamma}^{(i)}$$

但是这里有一个问题就是，对于函数间距来说，当w和b被替换成2w和2b时，$g(w^{T}x^{(i)}+b) = g(2w^{T}x^{(i)}+2b)$，这不会改变$h_{w,b}(x)$ 的值。所以为此我们引入几何间距：

考虑上图，直线为决策边界(由w,b决定)。向量w垂直于直线(为什么？$\theta^{T}x=0$，非零向量的内积为0，说明它们互相垂直)。假设A点代表样本$x^{(i)}$，它的类别为y=1。假设A点到决策边界的距离为$\gamma^{(i)}$，也就是线段AB。

那么，我们应该如何计算$\gamma^{(i)}$？
首先我们知道$w/\left \| w \right \|$ 表示的是在w方向上的单位向量。因为A点代表的是样本$x^{(i)}$，所以B点为：$x^{(i)}-\gamma^{(i)}\cdot w/\left \| w \right \|$。又因为B点是在决策边界上，所以B点满足$w^{T}x+b=0$，也就是：

$$w^{T}(x^{(i)}-\gamma^{(i)}\frac{w}{\left \| w \right \|})+b=0$$ 解方程得到：
$$\gamma^{(i)}=\frac{w^{T}x^{(i)}+b}{\left \| w \right \|}=\left ( \frac{w}{\left \| w \right \|} \right )^{T}x^{(i)}+\frac{b}{\left \| w \right \|}$$ 当然，上面这个方程对应的是正例的情况，反例的时候上面方程的解就是一个负数，这与我们平常说的距离不符合，所以我们乘上 $y^{(i)}$，即：
$$\gamma^{(i)}=y^{(i)}\left ( \left ( \frac{w}{\left \| w \right \|} \right )^{T}x^{(i)}+\frac{b}{\left \| w \right \|} \right )$$

可以看到，当$\left \| w \right \|=1$时，函数间距与几何间距就是一样的了。

同样，有了几何间距的定义，我们接下来就是要找所有点中间距最小的点了。对于给定的数据集$S = {(x^{(i)},y^{(i)});i=1,...,m}$，我们定义$\gamma$ 是数据集中函数间距最小的，即：

$$\gamma = \underset{i=1,...,m}{min}\gamma^{(i)}$$

讨论到这里，对于一组训练集，我们要找的就是看看哪个超平面的最近点的边距最大。因为这样我们的确信度是最大的。所以我们现在的问题就是：

$$\begin{aligned} & \underset{\gamma,w,b}{max} \ \gamma\\ &s.t.\ \ y^{(i)}(w^{T}x^{(i)}+b)\geq \gamma,\ i=1,...,m\\ &\left \| w \right \|=1 \end{aligned}$$ 这个问题就是说，我们想要最大化这个边距 $\gamma$，而且必须保证每个训练集得到的边距都要大于或等于这个边距 $\gamma$。 $\left \| w \right \|=1$保证函数边距与几何边距是一样的。但问题是 $\left \| w \right \|=1$这个东西很难搞，所以根据函数边距与几何边距之间的关系，我们变换一下问题：
$$\begin{aligned} & \underset{\hat{\gamma},w,b}{max} \ \frac{\hat{\gamma}}{\left \| w \right \|}\\ &s.t.\ \ y^{(i)}(w^{T}x^{(i)}+b)\geq \hat{\gamma},\ i=1,...,m \end{aligned}$$ 在这里，我们的目标是最大化 $\hat{\gamma}/\left \| w \right \|$,限制条件为所有的样本的函数边距要大于或等于 $\hat{\gamma}$。

写成这样子之后，我们还是没办法直接来求解这个问题，更没有办法写代码来实现训练。怎么办呢？

前面我们说过，对于函数间距来说，等比例缩放w和b不会改变$g(w^{T}x+b)$的值。因此，我们可以令$\hat{\gamma} = 1$，因为无论$\hat{\gamma}$的值是多少，我们都可以通过缩放w和b来使得$\hat{\gamma}$的值变为1。

所以最大化$\hat{\gamma}/ \left \| w \right \|=1/ \left \| w \right \|$(注意等号左右两边的w是不一样的)。
可能一开始很难理解为什么？其实对于上面的问题，如果那些式子都除以$\hat{\gamma}$，即变成：

$$\begin{aligned} & \underset{\hat{\gamma},w,b}{max} \ \frac{\hat{\gamma}/\hat{\gamma}}{\left \| w \right \|/\hat{\gamma}}\\ &s.t.\ \ y^{(i)}(w^{T}x^{(i)}+b)/\hat{\gamma}\geq \hat{\gamma}/\hat{\gamma},\ i=1,...,m \end{aligned}$$ 也就是：
$$\begin{aligned} & \underset{\hat{\gamma},w,b}{max} \ \frac{1}{\left \| w/\hat{\gamma} \right \|}\\ &s.t.\ \ y^{(i)}(w^{T}/\hat{\gamma} \cdot x^{(i)}+b/\hat{\gamma})\geq 1,\ i=1,...,m \end{aligned}$$ 然后我们令 $w=w/\hat{\gamma} , \ b= b/\hat{\gamma}$，问题就变成跟下面说的那样了。所以其实只是做了一个变量替换。
$$\begin{aligned} & \underset{\hat{\gamma},w,b}{max} \ \frac{1}{\left \| w \right \|}\\ &s.t.\ \ y^{(i)}(w^{T} x^{(i)}+b)\geq 1,\ i=1,...,m \end{aligned}$$

而最大化$1/\left \| w \right \|$相当于最小化$\left \| w \right \|^2$，所以我们的问题变成：

$$\begin{aligned} & \underset{\gamma,w,b}{min} \ \frac{1}{2}\left \| w \right \|^2\\ &s.t.\ \ y^{(i)}(w^{T}x^{(i)}+b)\geq 1,\ i=1,...,m \end{aligned}$$
现在，我们把问题转换成一个可以有效求解的问题了。上面的优化问题就是一个典型的二次凸优化问题，这种优化问题可以使用QP(quadratic programming )来求解。但是上面的问题有着特殊结构，通过 Lagrange Duality 变换到对偶变量 (dual variable) 的优化问题之后，可以找到一种更加有效的方法来进行求解，而且通常情况下这种方法比直接使用通用的 QP 优化包进行优化要高效得多。也就说，除了用解决QP问题的常规方法之外，还可以应用拉格朗日对偶性，通过求解对偶问题得到最优解，这就是线性可分条件下支持向量机的对偶算法，这样做的优点在于：一是对偶问题往往更容易求解；二者可以自然的引入核函数，进而推广到非线性分类问题。

那么如何使用拉格朗日乘子来高效求解这个问题呢？我们下一篇博客再来讲解。