迄今为止,我们所研究的所有算法几乎都是多项式时间的算法:对于规模为n的输入,在最坏情况下的运行时间是O(n^k),其中k为某一确定的常数。
如果一个判定问题的复杂度是该问题的一个实例的规模n的多项式函数,则这种可以在多项式时间内解决的判定性问题属于P类问题。P类问题就是所有复杂度为多项式时间的问题集合。通俗地称所有复杂度为多项式时间的问题为易解问题的问题类,否则为难解问题。
关于多项式时间。什么是多项式?小学时就接触过这样的方程式...
ax+b=0,ax^2+bx+c=0
第一,虽然把所需运行时间为O(n^100)的问题作为“难处理问题”也有其合理之处,但实际中却只有极少数问题需要如此高次的多项式时间,且经验表明,一旦某一问题的第一个多项式时间算法被发现后,往往跟着就会发现更为有效的算法。第二,对很多合理的计算模型来说,在一个模型上用多项式时间可解决的问题,在另一个模型上也可以在多项式时间内解决。第三,由于在加法、乘法和组合运算下多项式是封闭的,因此,多项式时间可解问题具有很好的封闭性。
反之,非多项式时间一般指指数增长模式,或更复杂模式。
然而有些问题很难找到多项式时间的算法(或许根本不存在)。但是如果给了该问题的答案,可以在多项式时间内判定这个答案是否正确。这种可以在多项式时间内验证一个解是否正确的问题称为NP问题(Non-deterministic Polynomial),亦称为易验证问题类。
简单地说,存在多项式时间的算法的一类问题,称之为P类问题;至今没有找到多项式算法解的一类问题,称之为NP类问题。
复杂性理论中最具有理论意义的当数NP完全性问题(NPC问题)。所谓“NPC完全性(NP-completeness)”问题是这样一个问题:由于“P=NP是否成立”这个问题难以解决,从NP类的问题中分出复杂性最高的一个子类,把它叫做NP完全类。
已经证明,任取NP类中的一个问题,再任取NP完全类中的一个问题,则一定存在一个具有多项式时间复杂性的算法,可以把NP类问题转化为NP完全类问题。这就表明,只要能证明NP完全类中有一个问题是属于P类的,也就证明了NP类中的所有问题都是P类的,即证明了P=NP。
已经被证明的NPC问题有哪些?
1. 团问题
每一对顶点之间都有一条边连接起来,这样的结构称为团。求最大团问题是NPC问题。
2.顶点覆盖问题
确定某个点后,与这个点相连接的顶点都称为被该顶点覆盖了。求最少个数确定点使整个图都被覆盖问题也是NPC问题。
3.哈密尔顿回路问题
找到一条路,将一个图上的所有顶点,不重复的走一遍,再回到起点。也是NPC问题。
4.旅行商问题
和哈密尔顿回路问题差不多,就是每条边上增加了一个权值。同样是NPC问题。
如何证明一个问题是否为NPC问题?
1.首先证明该问题为NP问题,即多项式时间内可验证的。
2.找到一种NPC问题以及一种多项式时间内的规约算法,将NPC问题规约为待证问题。
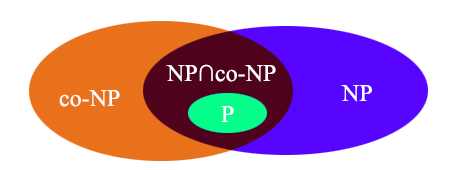
另外,把NP类问题的补集视为co-NP,那么是否有co-NP=NP?一般认为有如下关系...
何为NP困难问题(NP-hard)?NP-hard定义是这样的:
1.如果所有NP问题在多项式时间内都能规约到此问题;
2.但此问题不一定是NP问题。
同时已经证明了,所有的NP类问题都可以多项式规约到任何一个NP-hard问题。正如上文中提到“只要能证明NP完全类中有一个问题是属于P类的,也就证明了NP类中的所有问题都是P类的”。那么,此处也可利用NP-hard与NPC问题的关系将NPC问题进行转换,可很容易验证某个NPC问题的解的正确性。
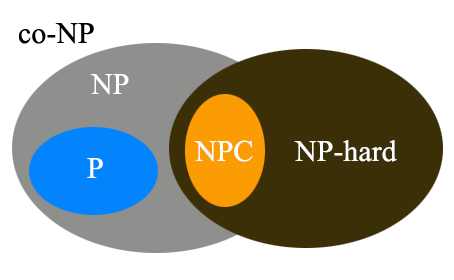
综上,在现阶段大多数理论计算机科学家们眼中的P、NP和NPC三者之间的关系是这样的,P和NPC都完全包含在NP内,且P∩NPC=∅。总之,P问题一定是NP问题,NPC问题一定为NP问题,NPC问题也一定为NP-hard问题。但是,NP-hard问题不一定为NPC问题,同样P?=NP也待证明。
通常可以从以下几个方面来寻求解决办法:
1.动态规划与分支限界方法:对于许多NP完全问题来说,用动态规划和分支限界方法常可以得到较高的解题效率。2.概率分析:对于许多NP完全问题,其困难实例出现的概念率很小,因此对这类NP完全问题常可以设计出平均性能很好的算法。
3.近似算法:通常可以设计出解NP完全问题的多项式时间的近似算法,以近似解来代替最优解。
4.启发式算法:在用别的方法都不能奏效时,也可以采用启发式算法来解NP完全问题。这类方法根据具体问题的启发式搜索策略来求问题的解,在实际使用时可能很有效,但有时很难说清楚它的道理。