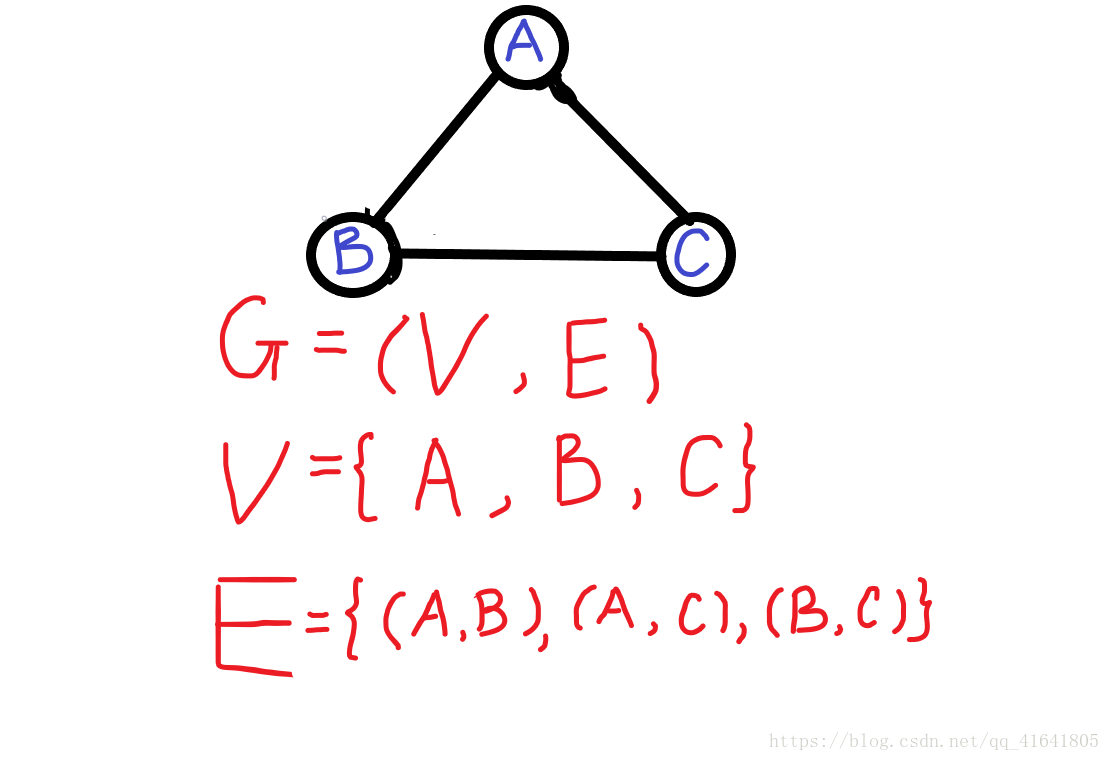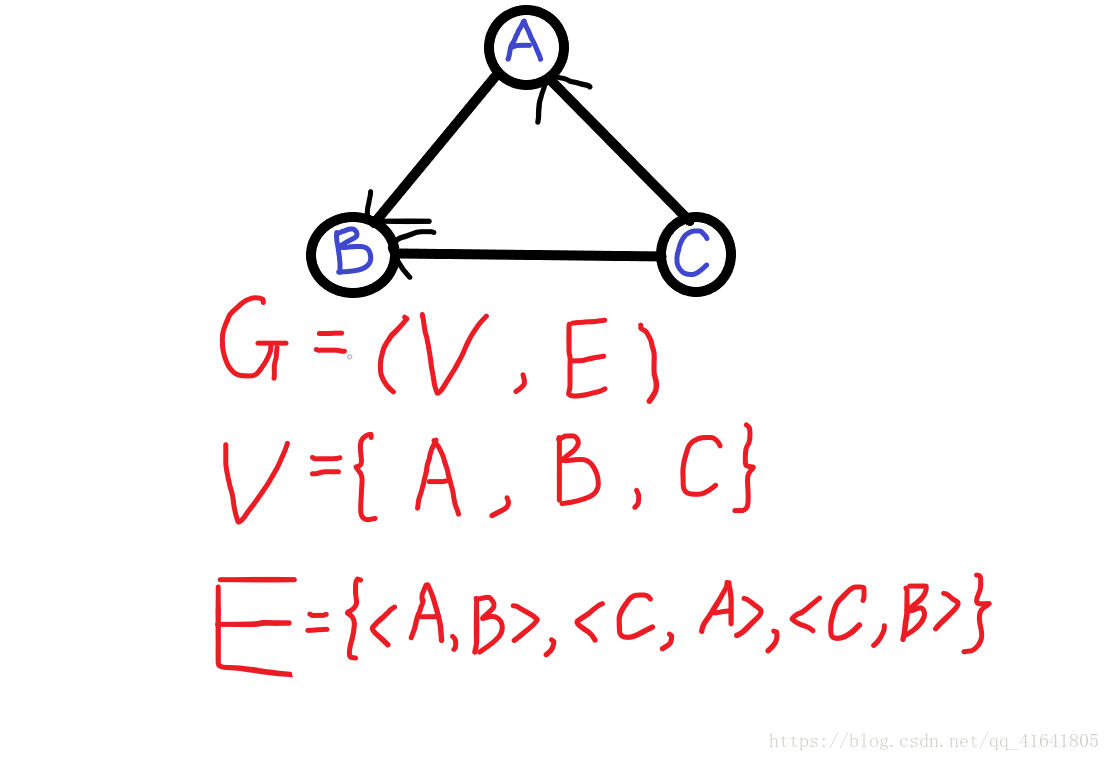版权声明：本文为博主原创文章，未经博主允许不得转载 https://blog.csdn.net/qq_41641805/article/details/81867329
一、基本概念
定义：图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为G（V,E），其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。简单概括，图=边集+点集，其中，点集不可为空，但边集可为空。
理解：1、数据元素在线性表中叫元素，在树中叫结点，在图中叫顶点
2、存在空表，空树，不存在空图。图结构强调顶点集合有穷非空。
3、线性表中，相邻的数据元素之间具有线性关系；树中，相邻两层的结点之间具有层次关系；图中，任意两个顶点之间都 可能有关系，顶点之间的逻辑关系用边来表示，但边集可为空。
二、术语
1、无向边：若顶点Vi与Vj之间的边没有方向，则称（Vi，Vj）为无向边
2、有向边：若从顶点Vi到Vj的边有方向，则称<Vi，Vj>为有向边，其中，Vi为弧尾，Vj为弧头
3、简单图
- 没有环，就是自己不会指向自己
- 没有平行边，就是两个顶点间最多只有一条边
4、无向完全图
- 无向图中，任意两个顶点之间有且仅有一条边
- 含有n个顶点的无向完全图有 n*(n -1)/2 条边
5、有向完全图
- 有向图中，任意两个顶点之间都存在方向相反的两条弧
- 含有n个顶点的有向完全图有 n*(n-1) 条边
6、稀疏图和稠密图
边或弧数< n*logn（n为顶点个数）：稀疏图
反之为稠密图
7、网：带权的图
8、子图：若G1=(V1,E1)，G2=(V2,E2)，且，
，则称G2为G1的子图
三、顶点与边之间的关系
1、无向图
- 对于无向图G=(V,E)，如果(V1,V2)
E，则称V1，V2互为邻接点，即V1，V2相邻接，边(V1,V2)依附于顶点V1，V2，边(V1,V2)与顶点V1，V2相关联
- 顶点的度：与该顶点相关联的边的数目，记为TD（V）
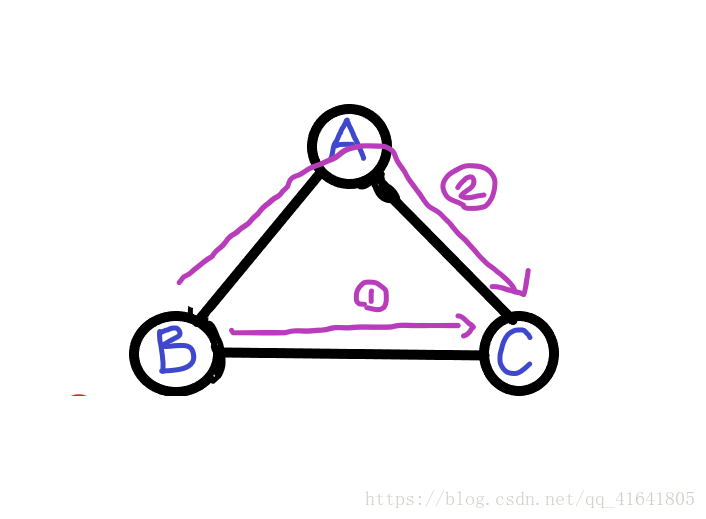
- 路径（如图示，从B到C有两条路径），路径长度=路径上边的数目
- 连通图 ：如果顶点V1到顶点V2有路径，则称V1和V2是连通的；如果图中任意两个顶点Vi和Vj都是连通的，则称G是连通图
- 连通分量：无向图中极大连通子图称为连通分量（首先要是子图，子图还要是连通的，含有极大顶点数，极大不是最大！一个图可以有多个连通分量）
- 连通图的生成树：极小连通子图，含有图中全部n个顶点，n-1条边（但是具有n个顶点，n-1条边的图不一定是生成树）
2、有向图
- 对于有向图G=(V,E)，如果<V1,V2>
- 入度：以该顶点为弧头的弧的数目，记为ID(V）
出度：以该顶点为弧尾的弧的数目，记为OD(V)
因此顶点V的度 TD(V)=ID(V)+OD(V)
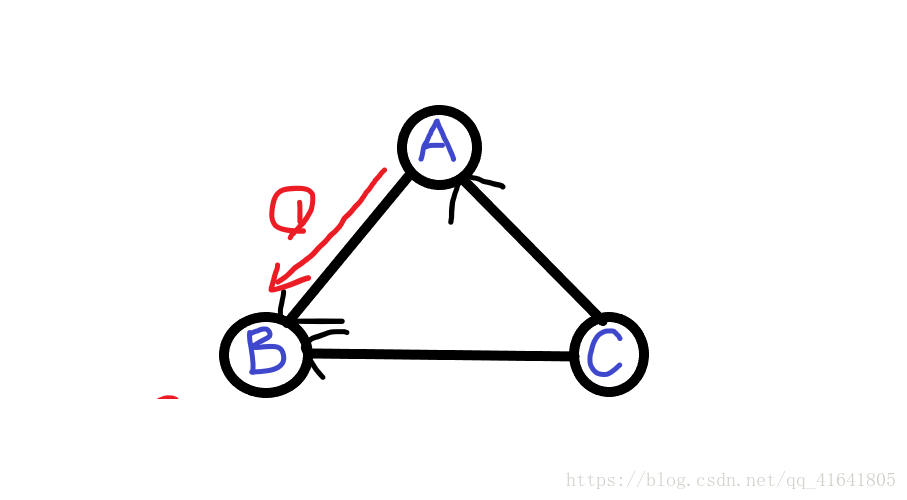
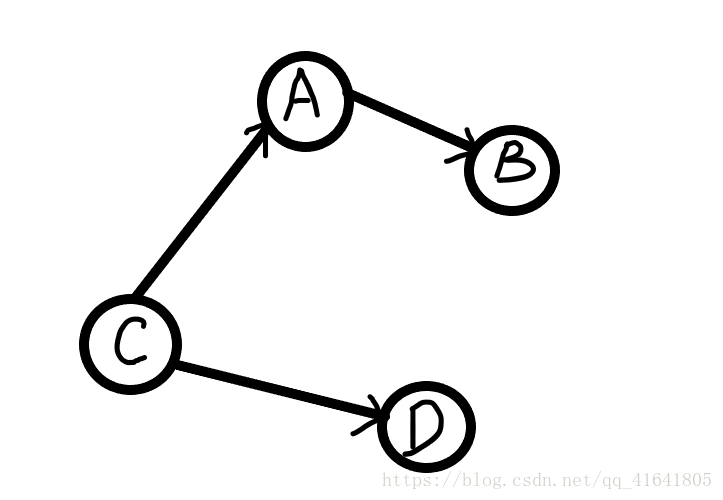
- 路径（如图示，从A到B只有一条路径，从B到C没有路径！按弧的走向），路径的长度=路径上弧的数目
- 强连通图： 有向图中，如果对每一对Vi到Vj都存在路径，则称为强连通图
- 强连通分量：有向图中的极大强连通子图称为有向图的强连通分量
- 有向树：有向图恰有一个顶点入度为0，其余顶点入度均为1
BY ZJQ