R之组间差异的非参数检验

# t 检验
# 在研究中最常见的行为就是对两个组进行比较。接受某种新药治疗的患者是否较使用某种现
# 有药物的患者表现出了更大程度的改善？某种制造工艺是否较另外一种工艺制造出的不合格品
# 更少？两种教学方法中哪一种更有效？如果你的结果变量是类别型的，那么可以直接使用7.3节
# 中阐述的方法。这里我们将关注结果变量为连续型的组间比较，并假设其呈正态分布。
# 为了阐明方法，我们将使用MASS包中的UScrime数据集。它包含了1960年美国47个州的刑
# 罚制度对犯罪率影响的信息。我们感兴趣的结果变量为Prob（监禁的概率）、U1（14~24岁年龄
# 段城市男性失业率）和U2（35~39岁年龄段城市男性失业率）。类别型变量So（指示该州是否位

# 于南方的指示变量）将作为分组变量使用。数据的尺度已被原始作者缩放过

library(MASS)

独立样本的t检验
如果你在美国的南方犯罪，是否更有可能被判监禁？我们比较的对象是南方和非南方各州，
因变量为监禁的概率。一个针对两组的独立样本t检验可以用于检验两个总体的均值相等的假设
这里假设两组数据是独立的，并且是从正态总体中抽得。检验的调用格式为:

  
t.test(y~X,data)

其中的y是一个数值型变量，x是一个二分变量

t.test(y1,y2)

其中的y1和y2为数值型向量（即各组的结果变量）。可选参数data的取值为一个包含了这些
变量的矩阵或数据框,里的t检验默认假定方差不相等，并使
用Welsh的修正自由度。你可以添加一个参数var.equal=TRUE以假定方差相等，并使用合并方
差估计。默认的备择假设是双侧的（即均值不相等，但大小的方向不确定）。你可以添加一个参
数alternative="less"或alternative="greater"来进行有方向的检验。

我们使用了一个假设方差不等的双侧检验，比较了南方（group 1）和非南
方（group 0）各州的监禁概率

t.test(Prob~So,data = UScrime)

# 
# > t.test(Prob~So,data = UScrime)
# 
# Welch Two Sample t-test
# 
# data:  Prob by So
# t = -3.8954, df = 24.925, p-value = 0.0006506
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
#   -0.03852569 -0.01187439
# sample estimates:
#   mean in group 0 mean in group 1 
# 0.03851265      0.06371269

你可以拒绝南方各州和非南方各州拥有相同监禁概率的假设（p < .001）。

非独立样本的t检验
再举个例子，你可能会问：较年轻（14~24岁）男性的失业率是否比年长（35~39岁）男性的
失业率更高？在这种情况下，这两组数据并不独立。你不能说亚拉巴马州的年轻男性和年长男性
的失业率之间没有关系。在两组的观测之间相关时，你获得的是一个非独立组设计（dependent
groups design）。前—后测设计（pre-post design）或重复测量设计（repeated measures design）同样
也会产生非独立的组。
非独立样本的t检验假定组间的差异呈正态分布,对于本例，检验的调用的格式为:

t.text(y1,y2,pairred=TRUE)

其中的y1和y2为两个非独立组的数值向量

sapply(UScrime[c("U1","U2")],function(x){c(mean=mean(x),sd=sd(x))})

with(UScrime,t.test(U1,U2,paired = TRUE))

# 
# > sapply(UScrime[c("U1","U2")],function(x){c(mean=mean(x),sd=sd(x))})
# U1       U2
# mean 95.46809 33.97872
# sd   18.02878  8.44545
# > with(UScrime,t.test(U1,U2,paired = TRUE))
# 
# Paired t-test
# 
# data:  U1 and U2
# t = 32.407, df = 46, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
#   57.67003 65.30870
# sample estimates:
#   mean of the differences 
# 61.48936

差异的均值（61.5）足够大，可以保证拒绝年长和年轻男性的平均失业率相同的假设。
年轻男性的失业率更高。事实上，若总体均值相等，获取一个差异如此大的样本的概率小于
0.000 000 000 000 000 22（即2.2e16）

组间差异的非参数检验
如果数据无法满足t检验或ANOVA的参数假设，可以转而使用非参数方法
两组的比较
若两组数据独立，可以使用Wilcoxon秩和检验（更广为人知的名字是Mann–Whitney U检验）
来评估观测是否是从相同的概率分布中抽得的（即，在一个总体中获得更高得分的概率是否比另
一个总体要大）。调用格式为：wilcox.text(y~x,text)
其中的y是数值型变量，而x是一个二分变量:wilcox.test(y1,y2)
其中的y1和y2为各组的结果变量。可选参数data的取值为一个包含了这些变量的矩阵或数据框。默
认进行一个双侧检验。你可以添加参数exact来进行精确检验，指定alternative="less"或
alternative="greater"进行有方向的检验。

如果你使用Mann–Whitney U检验回答上一节中关于监禁率的问题，将得到这些结果：

with(UScrime,by(Prob,So,median))
# > with(UScrime,by(Prob,So,median))
# So: 0
# [1] 0.038201
# ------------------------------------------------------------------ 
#   So: 1
# [1] 0.055552
# > 

wilcox.test(Prob~So,data = UScrime)
# 
# 你可以再次拒绝南方各州和非南方各州监禁率相同的假设（p < 0.001）
> wilcox.test(Prob~So,data = UScrime)
# 
# Wilcoxon rank sum test
# 
# data:  Prob by So
# W = 81, p-value = 8.488e-05
# alternative hypothesis: true location shift is not equal to 0
#

Wilcoxon符号秩检验是非独立样本t检验的一种非参数替代方法
它适用于两组成对数据和
无法保证正态性假设的情境。调用格式与Mann–Whitney U检验完全相同，不过还可以添加参数
paired=TRUE。让我们用它解答上一节中的失业率问题

sapply(UScrime[c("U1","U2")],median)
#> sapply(UScrime[c("U1","U2")],median)
# U1 U2 
# 92 34 

with(UScrime,wilcox.test(U1,U2,paired = TRUE))
# > with(UScrime,wilcox.test(U1,U2,paired = TRUE))
# 
# Wilcoxon signed rank test with continuity correction
# 
# data:  U1 and U2
# V = 1128, p-value = 2.464e-09
# alternative hypothesis: true location shift is not equal to 0

你再次得到了与配对t检验相同的结论.
多于两组的比较
在要比较的组数多于两个时，必须转而寻求其他方法。考虑7.4节中的state.x77数据集。
它包含了美国各州的人口、收入、文盲率、预期寿命、谋杀率和高中毕业率数据。如果你想比较
美国四个地区（东北部、南部、中北部和西部）的文盲率，应该怎么做呢？这称为单向设计（one-way
design），我们可以使用参数或非参数的方法来解决这个问题

如果无法满足ANOVA设计的假设，那么可以使用非参数方法来评估组间的差异

如果各组独立，则Kruskal—Wallis检验将是一种实用的方法
Kruskal–Wallis检验的调用格式为:kruskal.test(y~A,data)
其中的y是一个数值型结果变量，A是一个拥有两个或更多水平的分组变量（grouping variable）。
（若有两个水平，则它与Mann–Whitney U检验等价。

如果各组不独立（如重复测量设计或随机区组设计），那么Friedman检验会更合适
friedman.test(y~A|B,data)其中的y是数值型结果变量，A是一个分组变量，而B是一个用以认定匹配观测的区组变量（blocking
variable）

让我们利用Kruskal–Wallis检验回答文盲率的问题。首先，你必须将地区的名称添加到数据
集中。这些信息包含在随R基础安装分发的state.region数据集中:

states<-as.data.frame(cbind(state.region,state.x77))

kruskal.test(Illiteracy~state.region,data = states)

# > kruskal.test(Illiteracy~state.region,data = states)
# 
# Kruskal-Wallis rank sum test
# 
# data:  Illiteracy by state.region
# Kruskal-Wallis chi-squared = 22.672, df = 3, p-value = 4.726e-05

显著性检验的结果意味着美国四个地区的文盲率各不相同（p <0.001）
虽然你可以拒绝不存在差异的原假设，但这个检验并没有告诉你哪些地区显著地与其他地区
不同。要回答这个问题，你可以使用Mann–Whitney U检验每次比较两组数据。一种更为优雅的
方法是在控制犯第一类错误的概率（发现一个事实上并不存在的差异的概率）的前提下，执行可
以同步进行的多组比较，这样可以直接完成所有组之间的成对比较。npmc包提供了所需要的非
参数多组比较程序

install.packages("npmc")
var<-state.x77[,c("Illiteracy")]
mydata<-as.data.frame(cbind(class,var))
rm(class,var)
library(npmc)
summary(npmc(mydata),type="BF")

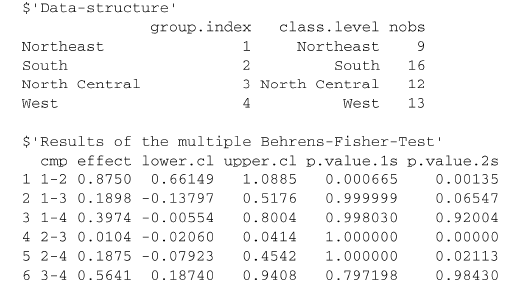
注意：npmc 包已经被弃用了！！！
但是下面的截图是以前没有弃用时的图

R之组间差异的非参数检验

猜你喜欢