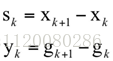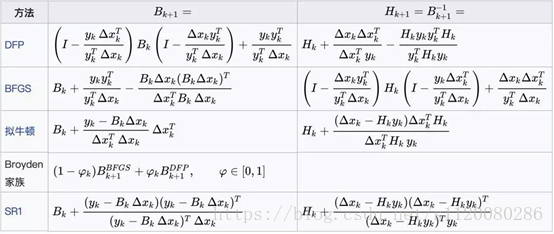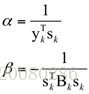机器学习算法中经常碰到非线性优化问题,如 Sparse Filtering 算法,其主要工作在于求解一个非线性极小化问题。在具体实现中,大多调用的是成熟的软件包做支撑,其中最常用的一个算法是 L-BFGS。为了解这个算法的数学机理,这几天做了一些调研,现把学习过程中理解的一些东西整理出来。
求函数的根
牛顿法的最初提出是用来求解方程的根的。我们假设点x∗为函数f(x)的根,那么有f(x∗)=0。现在我们把函数f(x)在点xk处一阶泰勒展开有:
f(x)=f(xk)+f′(xk)(x−xk)
那么假设点xk+1为该方程的根,则有
f(xk+1)=f(xk)+f′(xk)(xk+1−xk)=0
那么就可以得到
xk+1=xk−f(xk)/f′(xk)
这样我们就得到了一个递归方程,我们可以通过迭代的方式不断的让x趋近于x∗从而求得方程f(x)的解。
最优化
对于最优化问题,其极值点处有一个特性就是在极值点处函数的一阶导数为0。因此我们可以在一阶导数处利用牛顿法通过迭代的方式来求得最优解,即相当于求一阶导数对应函数的根。
首先,我们对函数在xk点处进行二阶泰勒展开
f(x)=f(xk)+f′(xk)(x−xk)+1/2f′′(xk)(x−xk)2⇒
(f(x)−f(xk))/(x−xk)=f′(xk)+f′′(xk)(x−xk)
因此,当x→xk时,f′(x)=f′(xk)+f′′(xk)(x−xk)。这里假设点xk+1是一阶导数的根,那么就有
f′(xk+1)=f′(xk)+f′′(xk)(xk+1−xk)=0
依据上式可以得到
xk+1=xk−f′(xk)/f′′(xk)
这样我们就得到了一个不断更新xx迭代求得最优解的方法。这个也很好理解,假设我们上面的第一张图的曲线表示的是函数f(x)一阶导数的曲线,那么其二阶导数就是一阶导数对应函数在某点的斜率,也就是那条切线的斜率,那么该公式就和上面求根的公式本质是一样的。
牛顿法求最优值的步骤如下:
1. 随机选取起始点x0;
2. 计算目标函数f(x)在该点xk的一阶导数和海森矩阵;
3. 依据迭代公式更新x值
如果E(f(xk+1)−f(xk))<ϵ,则收敛返回,否则继续步骤2,3直至收敛
我们可以看到,当我们的特征特别多的时候,求海森矩阵的逆的运算量是非常大且慢的,这对于在实际应用中是不可忍受的,因此我们想能否用一个矩阵来代替海森矩阵的逆呢,这就是拟牛顿法的基本思路。
在牛顿法的求解过程中,首先是将函数在
处展开,展开式为:
其中,,表示的是目标函数在
的梯度,是一个向量。
,表示的是目标函数在
处的Hesse矩阵。省略掉最后面的高阶无穷小项,即为:
上式两边对求导,即为:
在基本牛顿法中,取得最值的点处的导数值为,即上式左侧为
。则:
求出其中的:
如果令:
上式可以简写为:
即:
这个条件称为拟牛顿条件,用来近似代替Hessian矩阵的矩阵需要满足此条件。根据此条件,构造出了多种拟牛顿法,典型的有DFP算法、BFGS算法、L-BFGS算法等,在这里我们重点介绍BFGS算法。下图列出了常用的拟牛顿法的迭代公式(图片来自维基百科)
BFGS算法是它的四个发明人Broyden,Fletcher,Goldfarb和Shanno名字首字母的简写。算法的思想是构造Hessian矩阵的近似矩阵:
并迭代更新这个矩阵:
该矩阵的初始值为单位阵I。这样,要解决的问题就是每次的修正矩阵
的构造。其计算公式为:
其中:
因此有:
算法的完整流程为:
1.给定优化变量的初始值和精度阈值ε,令
,
2.确定搜索方向
3.搜索得到步长
4.如果,则迭代结束
5.计算
6.计算
7.令,返回步骤2
下面来看源代码实现。函数solve_l1r_l2_svc实现求解L1正则化L2损失函数支持向量机原问题的坐标下降法。在这里我们重点看牛顿方向的计算,直线搜索,参数更新这三步,其他的可以忽略掉。代码如下: