垃圾邮件分类
任务要求
使用文件spambase.data中的数据,训练垃圾邮件分类的贝叶斯分类器,并测试分类性能。
数据初步分析
spambase.data是一个垃圾邮件的数据库,来自于惠普公司的Hewlett Packard Labs实验室,采集时间是1999年的6~7月份。
该数据库中包含了4601个样本,其中1813条为垃圾邮件(spam);每个样本有58个属性。在数据文件中,每行为一个样本,58个属性按顺序排列,使用","分隔。格式如下:
图 21 数据文件的格式
各属性的含义和数值范围如下表所列:
表格 21 样本属性说明
属性序号 |
含义 |
范围 |
最大值 |
1-48 |
特定单词的出现频率 |
[0, 100] |
<100 |
49-54 |
特定字符的出现频率 |
[0, 100] |
<100 |
55 |
大写字母游程均长 |
[1, …] |
1102.5 |
56 |
最长大写字母游程 |
[1, …] |
9989 |
57 |
大写字母游程总长 |
[1, …] |
15841 |
58 |
垃圾邮件标识(1代表垃圾邮件) |
{0, 1} |
1 |
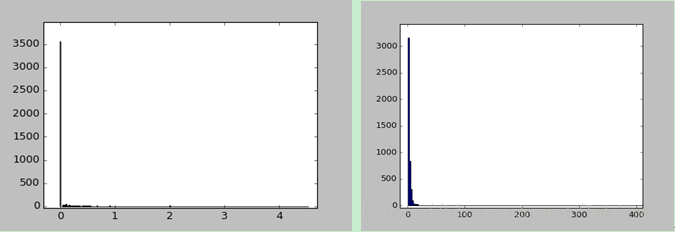
第1-54属性可以看成统计特性相似的一类,因为它们都代表了单词或字符的出现频率,范围都是[0, 100]. 考察第1个属性的分布规律,对全部4601个样本做频数统计,如图2-1(a), 可见大部分样本的值为0,还有少部分分布在1以内,均值在零点几左右。
同样,第55~57个属性的统计特性应当是一致的,都表示游程的长度。对第55个属性的数值作频数统计,如图2-1(b), 虽然数值的分布范围很大,但主要集中分布在数值较小的区域。
图 22 (a)属性1的数值分布, (b)属性55的数值分布
显然,这样的分布不能用高斯分布或其他分布函数来表示。所以可以建立离散的概率密度函数,用样本的频数估计概率密度。
频数统计首先确定组距,或者称之为量化阶:
\[Quantization\_order = \frac{{Max - Min}}{{Bins}}\]
其中,Max是可接受数据的最大值,min是最小值,Bins为组数。
然后建立频数表,其长度就是组数Bins。遍历待统计的数据,判断每个数据落入何组中,频数表中对于的数值就加1.
如果要得到概率,只需将频数除以总样本数。
贝叶斯分类器
原理:
贝叶斯分类是一种有监督的分类方法。其原理如下:首先统计各类的先验概率,以及类条件概率分布,然后通过贝叶斯公式:
\[P({\omega _i}|{\mathbf{x}}) = \frac{{P({\mathbf{x}}|{\omega _i}) \cdot P({\omega _i})}}{{P({\mathbf{x}})}} = \frac{{p({\mathbf{x}}|{\omega _i})d{\mathbf{x}} \cdot P({\omega _i})}}{{p({\mathbf{x}})d{\mathbf{x}}}} = \frac{{p({\mathbf{x}}|{\omega _i}) \cdot P({\omega _i})}}{{p({\mathbf{x}})}}\]( 1)
可以利用已知量转换得到后验概率 $P({\omega _i}|{\bf{x}})$,即表示在特征x时属于类${\omega _i}$ 的概率分布。
从式(1)还可以看出,因为 $P({\bf{x}}|{\omega _i})$=$p({\bf{x}}|{\omega _i})d{\bf{x}}$,分子分母同时消去后,后验概率分布实际上也可以通过先验概率密度来计算。而且实际上,$p({\bf{x}}|{\omega _i})$ 比$P({\bf{x}}|{\omega _i})$更容易表示,所以一般使用$p({\bf{x}}|{\omega _i})$计算后验概率。
朴素贝叶斯
如果样本的特征向量x维数很大,会给条件概率密度函数$p({\bf{x}}|{\omega _i})$的求取带来困难。假设各属性的值相互独立,则$p({\bf{x}}|{\omega _i})$可以表示为:
$$p({\bf{x}}|{\omega _i}) = \prod p({x_k}|{\omega _i})$$(2)
将式(2)代入式(1),就得到了朴素贝叶斯的表达式:
$$P({\omega _i}|{\bf{x}}) = \frac{{\prod p({x_k}|{\omega _i}) \cdot P({\omega _i})}}{{p({\bf{x}})}} = $$(3)
而$\prod p({x_k}|{\omega _i})$中的每一项,可以使用第2节中所说的频数进行估计。
决策规则
对于两类分类问题,根据后验概率的大小判决所属分类,即:
$$P({\omega _1}|{\bf{x}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \matrix
> \\
< \\
\endmatrix {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P({\omega _2}|{\bf{x}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Rightarrow {\bf{x}} \in \matrix
{{\omega _1}} \\
{{\omega _2}} \\
\endmatrix $$
基于上式,代入贝叶斯公式,由于分母都一样,可以得到变换形式的决策式:
$$p({\bf{x}}|{\omega _1}){\kern 1pt} {\kern 1pt} P({\omega _1}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \matrix
> \\
< \\
\endmatrix {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P({\bf{x}}|{\omega _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P({\omega _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Rightarrow {\bf{x}} \in \matrix
{{\omega _1}} \\
{{\omega _2}} \\
\endmatrix $$(4-a)
$$\frac{{p({\bf{x}}|{\omega _1}){\kern 1pt} {\kern 1pt} }}{{P({\bf{x}}|{\omega _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} }}{\kern 1pt} {\kern 1pt} \matrix
> \\
< \\
\endmatrix {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{P({\omega _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} }}{{P({\omega _1}){\kern 1pt} {\kern 1pt} }} \Rightarrow {\bf{x}} \in \matrix
{{\omega _1}} \\
{{\omega _2}} \\
\endmatrix $$(4-b)
$$\ln \left( {\frac{{p({\bf{x}}|{\omega _1}){\kern 1pt} {\kern 1pt} }}{{P({\bf{x}}|{\omega _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} }}} \right){\kern 1pt} {\kern 1pt} \matrix
> \\
< \\
\endmatrix {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ln \left( {\frac{{P({\omega _2}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} }}{{P({\omega _1}){\kern 1pt} {\kern 1pt} }}} \right){\kern 1pt} \Rightarrow {\bf{x}} \in \matrix
{{\omega _1}} \\
{{\omega _2}} \\
\endmatrix $$(4-c)
他们都是等价的,针对不同的后验概率形式,选择最简单的表达式即可。在本题中,使用4-a更方便。
程序设计
通过上述原理的分析,该题的主要计算工作可以分为4步,用顺序结构即可实现。框图归纳如下:
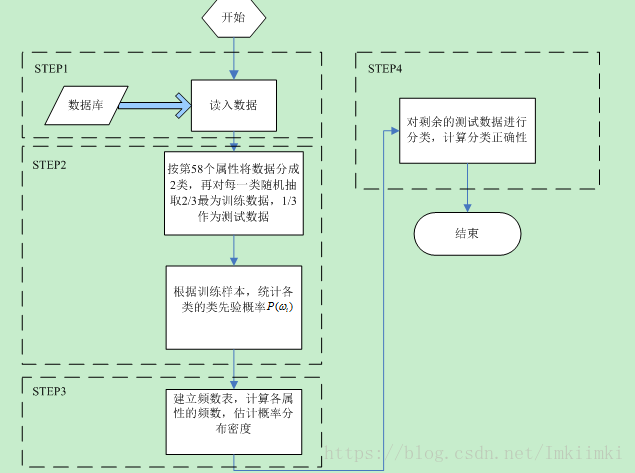
图 41程序流程图
图中标注的步骤编号与程序源码中的注释相对应。
编程实现
程序按照框图中的4个主要步骤设计。为了将更清楚地显示运行过程,在相同目录下建立了一个文本文件Tracking.log,每一个Step执行完成后,使用file.write()函数在文件中写入运行时间戳和运行结果。
创建文本文件的代码如下,使用写入模式w,若不存在则创建,若已存在同名文件,会清空内容后重新创建。
file= open('Tracking.log','w',buffering=100)#创建一个文件,用于写入运行报告
Step1读入数据,并统计长度
spambase.data中的数据一行有58个,用","分隔。使用numpy的loadtxt()函数可以直接读入,返回一个array对象属性。然后使用array.shape方法得到数据的维度。
original_data_readin = np.loadtxt("spambase.data", dtype=float, delimiter=",")
size = original_data_readin.shape
sampleNums_of_classALl = size[0];#样本总数
sampleNums_of_class_spam=int(sum(original_data_readin[:,-1]))#统计属于垃圾邮件的样本数量(1813)
sampleNums_of_class_good= sampleNums_of_classALl - sampleNums_of_class_spam #正常邮件的数量
length_of_attributes = size[1];#属性向量的长度(应该是58)
程序执行后,original_data_readin变量中存储了读取的原始数据, sampleNums_of_classALl是所有样本的数量,sampleNums_of_class_spam是垃圾邮件样本数量,sampleNums_of_class_good是正常邮件的样本数量,length_of_attributes是特征属性长度。
Step2随机产2/3的数据用于训练,并计算类先验概率
这一部分位于源码的line49-70.
所给的数据库中,垃圾邮件和非垃圾邮件已经分类,前面是垃圾邮件,后面是非垃圾邮件。以垃圾邮件中产生2/3训练样本为例,说明随机抽取的方法:
遍历所有垃圾邮件样本,使用random.uniform(0,3)函数产生0-3均匀分布的随机数,与1比较,如果小于1,归类为测试样本;大于等于1,则归类为训练样本。将垃圾邮件的训练样本存入矩阵sampls_spam_train,测试样本存入sampls_spam_test.
同理,对正常邮件也进行2/3随机抽取,训练样本存入矩阵sampls_good_train,测试样本存入sampls_good_test.
随后,根据sampls_spam_train和sampls_good_train的长度,计算了类先验概率和.
文件Tracing.log中写入这一步的执行结果。
Step3 根据频数估计类条件概率
如第二节中所述,使用频数估计类条件概率密度。这里定义了一个函数:Hist_Estimate(data,bins, min,max,normal),具体如下:
defHist_Estimate(data=np.zeros((1,54)),bins=quant_order, min=0.0,max=100,normal=1):
#@对输入的数据进行频数估计,返回bins×data.shape[1]维的向量
deltaX=float(bins)/(max-min)
#print deltaX
pdf=np.zeros((bins,data.shape[1]))
for i in range(data.shape[1]):#pdf的列遍历
#print i
for j in range (data.shape[0]):#统计频数
#print str(i)+str(j)
pdf[int(deltaX*data[j,i]),i]+=1
if normal!=1:#返回不归一化的频数
return pdf
else:#返回归一化的频数,可以看作概率密度函数
return pdf/data.shape[0]
它实现了第2节中所述的频数统计功能,输入data是N*n的样本(N为样本数,n为特征数),bins量化阶数,min和max分别表示频数表的最小和最大值,normal=1返回归一化的频率,否则返回频数。返回值是一个bins*n的矩阵,每一列就是一个属性的频数(或频率)表。
由于样本中前54个属性的值范围为[0,100],而55,56,57三个属性的值从1到几千,所以使用对他们分两种情况求频数。调用Hist_Estimate()函数时,前者取min=0, max=100,后者的min=1, max=20000. 量化阶bins都取同样值,这样返回的频数表长度都是一样的。
pdf54_spam = Hist_Estimate(sampls_spam_train[:,:54],bins=quant_order)
pdf54_good = Hist_Estimate(sampls_good_train[:,:54],bins=quant_order)
pdf57_spam = Hist_Estimate(sampls_spam_train[:,54:57],min=0.0,max=20000,bins=quant_order)
pdf57_good = Hist_Estimate(sampls_good_train[:,54:57],min=0.0,max=20000,bins=quant_order)
pdf54_spam中存储了垃圾邮件类中前54个属性的频数表,pdf57_spam是后3个属性的频数表。非垃圾邮件也类似处理。
这部分的代码在line 84 – 103.
Step4 使用测试集数据对分类器作性能测试
通过之前的步骤,已经得到了类先验概率和类条件概率密度.由式(3)可以计算出后验概率,再根据式(4-a)做出决策。
函数Gx_Compute(data,px,bins, min,max)用于计算一个输入样本的各个属性的先验概率乘积,即. 由于有些值的概率密度为0,为了避免乘0后结果恒为0,加上了一个微小的常数0.001,所以实际上计算的是.函数Gx_Compute()的输入参数data是一个样本中某些属性组成的向量(1*nk),px是对于的频率表(bins*nk), bin是量化阶数,min和max是频率表中的最小值和最大值。
首先测试垃圾邮件的分类性能。调用函数Gx_Compute(),对sampls_spam_test中的一个样本,计算式(4-a)左右两项。由于57个属性分成了两种量化阶不同的统计,所以计算需要使用两次Gx_Compute(),计算也需要使用两次Gx_Compute(). 比较和的值,如果前者大,则判为垃圾邮件,即正确分类了,计数值amount_of_test_spam_correct加一。遍历完所有待测试垃圾邮件之后,计算正确识别的比例,即amount_of_test_spam_correct / amount_of_test_spam_total.
垃圾邮件分类测试的代码如下:
#对spam测试样本进行检验
amount_of_test_spam_total = sampls_spam_test.shape[0]
amount_of_test_spam_correct =0
for i in range(amount_of_test_spam_total):
if(Gx_Compute(sampls_spam_test[i,0:54],pdf54_spam)*Gx_Compute(sampls_spam_test[i,54:57],pdf57_spam,quant_order,0.0,20000)*Pw1>Gx_Compute(sampls_spam_test[i,0:54],pdf54_good)*Gx_Compute(sampls_spam_test[i,54:57],pdf57_good,quant_order,0.0,20000)*Pw2 ):
amount_of_test_spam_correct +=1
printu'垃圾邮件正确检出率'
print float(amount_of_test_spam_correct)/ amount_of_test_spam_total
检验正常邮件识别性能的方法与之相同,只是改变了输入样本,并反转判决条件。
这部分的代码位于line 124 – 145, 检测结果会打印在屏幕上,同时写入日志。
运行结果
使用pyinstaller工具打包编译成了单文件exe,将数据文件和程序放在同一目录下,运行exe。
图 61数据文件和编译得到的程序
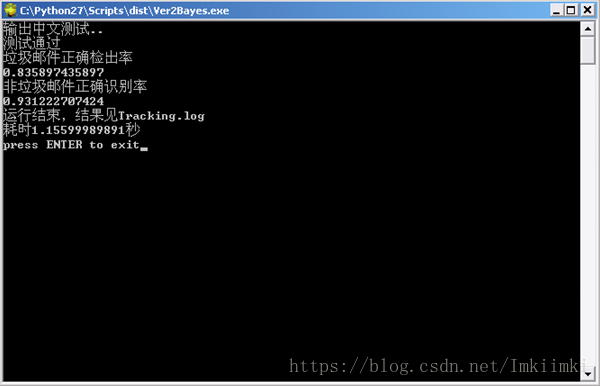
图 62 运行结果
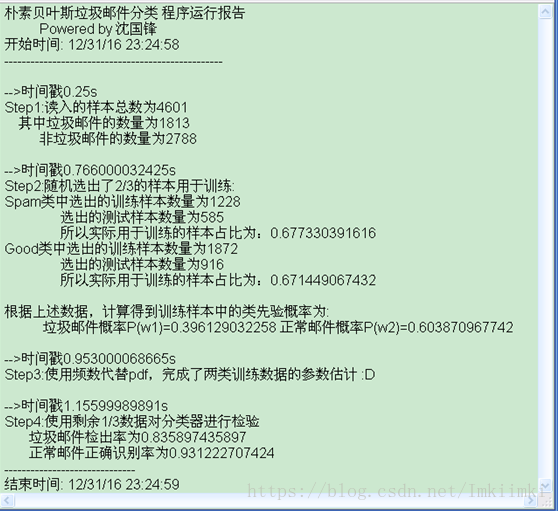
等待程序将所需的动态链接库解压到系统缓存后,就会执行python程序,本次运行,垃圾邮件检出率在0.83,正常邮件识别率在0.93,运行了大约1.15秒。打开目录下生成的Tracking.log文本文件,如下所示:
图 63 log文件
文件中记录了每步完成的时间,也记录了关键步骤的运算结果。从结果来看,程序功能是正确的。
总结
本次的编程过程比较顺利,写完一个步骤就进行验证,没有出现找很久Bug的情况。由于不涉及复杂矩阵运算,几乎所有的运算操作都是从0开始自己写的,没有使用别的库,也就没有参考程序。但这直接造成了程序冗长繁杂,写的有些随意,有些计算方法也不是最优的。幸好我认为变量定义还是很清楚的,看到名称可以大概想到其含义,否则就真的写完之后我自己也看不懂了。
在一开始写的时候,我感觉训练好分类器,然后检测一下分类结果,输出一个正确率,程序就结束了,似乎不是很直观,而且编写时也正好需要调试,突发奇想就想把关键步骤的执行结果写到文本文件里。后来又加了一个毫秒精度的时间戳,这样每一步执行了多少时间,都会写到日志里,这就很有意思了,看到日志似乎可以回顾程序的执行过程。
这次还使用了pyinstaller工具,将python程序编译成了exe,这样即使在没有安装python的计算机上也可以运行。
此外,还遇到了一些问题。首先是print语句打印中文乱码问题,表现为在IDLE的shell中是正常的,但在控制台中运行就会乱码。最后查找到原因是系统的编码与py2.7不同。这在python3中已经解决,但对于python2,需要对编码进行转换:
import sys
type = sys.getfilesystemencoding()
print '输出中文测试..'.decode('utf-8').encode(type)
或者在字符前加u,表示unicode编码:
print u'中文测试'
对于概率密度的计算,使用了频数进行估计。这就涉及到量化阶的问题,即把多大的范围看作一个频数统计区间。如果把量化阶取得过大,一些原本有差异的数值会落入同一个统计区间中,这样就使得模型的灵敏度降低,影响分类效果;但是如果量化阶取得过小,即频数分组很多,在有限的训练样本下,就会造成估计的失准,最后也影响分类准确率。程序中使用了500个量化值进行统计,效果较好。
取不同的频数量化组数,识别率变化如下,说明量化组数在200到1000内比较理想。
频数量化组数 |
垃圾邮件识别率 |
非垃圾邮件正确识别率 |
100 |
0.835820895522 |
0.891832229581 |
200 |
0.85641025641 |
0.929399367756 |
500 |
0.855687606112 |
0.949506037322 |
1000 |
0.809825673534 |
0.953241232731 |
1500 |
0.786991869919 |
0.93237704918 |
2000 |
0.802931596091 |
0.932584269663 |
3000 |
0.78813559322 |
0.924528301887 |
此外,垃圾邮件的识别率总是比正常邮件的识别率低,我就想到一句话:正常邮件都是相似的,垃圾邮件各有各的不同。
好了,写到这里正好跨年了,我就回去把第一页的日期也改了,祝大家新年快乐!