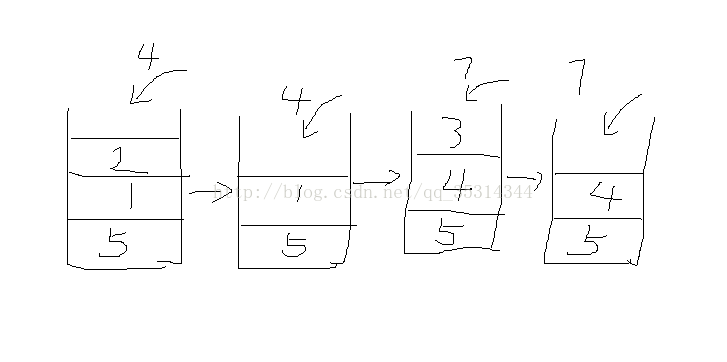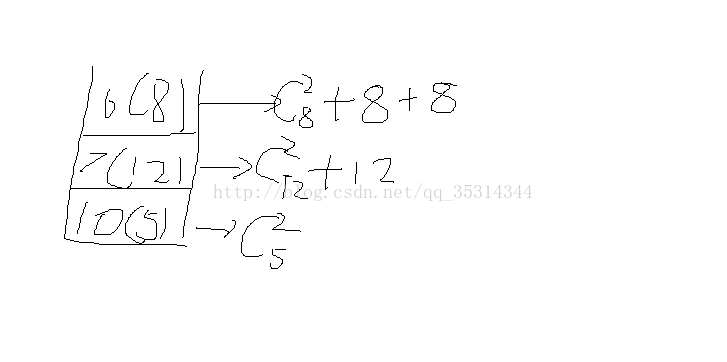窗口内最大值的更新结构和单调栈结构
一、窗口内最大值的更新结构及其扩展面试题目
介绍窗口以及窗口内最大值或最小值的更新结构(单调双向队列)
import java.util.LinkedList;
public class UpdateMax {
public static class UpdateDeque {
public LinkedList<Integer> deque;
public int[] arr;
public int L;
public int R;
public UpdateDeque(int[] arr) {
this.arr = arr;
deque = new LinkedList<Integer>();
L = 0;
R = -1;
}
public void addNumFromRight() {
if (R == arr.length - 1) {
throw new RuntimeException("no num to add");
}
while (!deque.isEmpty() && arr[deque.getLast()] <= arr[R + 1]) {
deque.pollLast();
}
deque.addLast(++R);
}
public void removeNumFromLeft() {
if (R == L - 1) {
throw new RuntimeException("no num to remove");
}
if (L == deque.peekFirst()) {
deque.pollFirst();
}
L++;
}
public int getMax() {
if (R == L - 1) {
throw new RuntimeException("no num");
}
return arr[deque.peekFirst()];
}
}
// public static void main(String[] args) {
// int[] arr = {4, 3, 5, 4, 3, 3, 6, 7};
// UpdateDeque updateDeque = new UpdateDeque(arr);
// }
}
题目:生成窗口最大值数组
描述:有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边,窗口每次向右滑一个位置。
例如,数组为【4,3,5,4,3,3,6,7】,窗口大小为3时:
【4,3,5】,4,3,3,6,7 窗口中最大值为5
4,【3,5,4】,3,3,6,7 窗口中最大值为5
4,3,【5,4,3】,3,6,7 窗口中最大值为5
4,3,5,【4,3,3】,6,7 窗口中最大值为4
4,3,5,4,【3,3,6】,7 窗口中最大值为6
4,3,5,4,3,【3,6,7】 窗口中最大值为7
如果数组长度为n,窗口大小为w,则一共产生n-w+1个窗口的最大值。
请实现一个函数:
输入:整型数组arr,窗口大小为w。

输出:一个长度为n-w+1的数组,res[i]表示每一种窗口状态下的最大值。
以本题为例,结果应该返回【5,5,5,4,6,7】。
思考:本题的关键在于利用双端队列实现窗口最大值的更新。首先生成双端队列qmax,qmax中存放数组arr中的下标。
假设遍历到arr[i],qmax的放入规则是:
- 如果qmax为空,直接把下标i放入qmax,放入过程结束
- 如果qmax不为空,取出当前qmax队尾存放的下标,假设为j
- 如果arr[j]>arr[i],直接把下标i放进qmax的队尾,放入过程结束。
- 如果arr[j]<=arr[i],把j从qmax中弹出,继续qmax的放入规则。
假设遍历到arr[i],qmax的弹出规则为:如果qmax对头的下标等于i-w,说明当前qmax队头的下标已过期,弹出当前对头的下标即可。
根据上面的放入和弹出规则,qmax便成了一个维护窗口w的子数组的最大值更新的结构。每个下标值最多进qmax一次,出qmax一次。所以遍历的过程中进出双端队列的操作是时间复杂度为O(N),整体的时间复杂度也为O(N)。
代码:
import java.util.LinkedList;
public class SlidingWindowsMaxArray {
public static int[] getMaxWindow(int[] arr, int w) {
if (arr == null || w < 1 || arr.length < w) {
return null;
}
LinkedList<Integer> qmax = new LinkedList<>();
int[] res = new int[arr.length - w + 1];
int index = 0;
for (int i = 0; i < arr.length; i++) {
while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[i]) {
qmax.pollLast();
}
qmax.addLast(i);
if (qmax.peekFirst() == i - w) {
qmax.pollFirst();
}
if (i >= w - 1) {
res[index++] = arr[qmax.peekFirst()];
}
}
return res;
}
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}
public static void main(String[] args){
int[] arr = {4,3,5,4,3,3,6,7};
printArray(getMaxWindow(arr,3));
}
}
题目:最大值减去最小值小于或等于num的子数组数量
描述:给定数组arr和整数num,共返回有多少个子数组满足如下情况:
max(arr[i....j])-min(arr[i....j])<=num
max(arr[i...j])表示子数组arr[i...j]中的最大值,min(arr[i...j])表示子数组arr[i...j]中的最小值。
要求:如果数组长度为N,请实现时间复杂度为O(N)的解法
思考:
普通的解法:找到arr的所有子数组,一共有个,然后对每一个子数组做遍历找到其中的最小值和最大值。这个过程时间复杂度为O(N),然后看看这个子数组是否满足条件。统计所有满足的子数组数量即可。普通解法的容易实现,但是时间复杂度为
。
本题使用双端队列解决。生成两个双端队列qmax和qmin。当子数组为arr[i...j]时,qmax维护了窗口子数组arr[i...j]的最大值更新的结构,qmin维护了窗口子数组arr[i...j]的最小值更新的结构。当子数组arr[i...j]向右扩一个位置变成arr[i...j+1]时,qmax和qmin结构可以在O(1)的时间内更新,并且可以在O(1)的时间内得到arr[i...j+1]的最大值和最小值。当子数组arr[i...j]向左缩一个位置变成arr[i+1....j]时,qmax和qmin结构依然可以在O(1)的时间内更新,并且在O(1)的时间内得到arr[i+1...j]的最大值和最小值。
通过分析题目满足的条件,可以得到如下两个结论:
- 如果子数组arr[i...j]满足条件,即max(arr[i....j])-min(arr[i....j])<=num,那么arr[i...j]中的每一个子数组,即arr[k...l](i<=k<=l<=j)都满足条件。以子数组arr[i...j-1]为例说明,arr[i...j-1]最大值只可能小于或等于arr[i...j]的最大值,arr[i...j-1]最小值只可能大于或等于arr[i...j]的最小值,所以arr[i...j-1]必然满足天剑。同理,arr[i...j]中的每一个子数组都满足条件。
- 如果子数组arr[i...j]不满足条件,那么所有包含arr[i...j]的子数组,即arr[k...l](i<=k<=l<=j)都不满足条件。
根据双端队列qmax和qmin的结构性质,以及如上两个结论,设计整个过程如下:
- 生成两个双端队列qmax和qmin,含义如上文所说。生成两个整型变量i和j,表示子数组的范围,即arr[i...j]。生成整型变量res,表示所有满足条件的子数组数量。
- 令j不断向右移动(j++),表示arr[i....j]一直向右扩大,并不断更新qmax和qmin结构,保证qmax和qmin始终维持动态窗口最大值和最小值的更新结构。一旦出现arr[i...j]不满足条件的情况,j向右扩的过程停止,此时arr[i...j-1]、arr[i...j-2]、arr[i...j-3]、...、arr[i...j]一定都是满足条件的。也就是说,所有必须以arr[i]作为第一个元素的子数组,满足条件的数量为j-i个。于是令res+=j-i。
- 当进行完步骤2,令i向右移动一个位置,并对qmax和qmin做出相应的更新,qmax和qmin从原来的arr[i...j]窗口变为arr[i+1...j]窗口的最大值和最小值的更新结构。然后重复步骤2,也就是求所有必须以arr[i+1]作为第一个元素的子数组中,满足条件的数量有多少个。
- 根据步骤2和步骤3,依次求出以arr[0]、arr[1]、...、arr[N-1]作为第一个元素的子数组中满足条件的数量分别有多少个,累加起来的数量就是最终的结果。
上述过程中,所有的下标值最多进qmax和qmin一次,出qmax和qmin一次。i和j的值也不断增加,并且从来不减少。所以整个过程的时间复杂度为O(N)。
代码:
import java.util.LinkedList;
public class AllLessNumSubArray {
public static int getNum(int[] arr, int num) {
if (arr == null || arr.length == 0) {
return 0;
}
LinkedList<Integer> qmin = new LinkedList<Integer>();
LinkedList<Integer> qmax = new LinkedList<Integer>();
int i = 0;
int j = 0;
int res = 0;
while (i < arr.length) {//i是开头
while (j < arr.length) {//j是窗口最右侧位置,再往右一个
while (!qmin.isEmpty() && arr[qmin.peekLast()] >= arr[j]) {
qmin.pollLast();
}
qmin.addLast(j);
while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[j]) {
qmax.pollLast();
}
qmax.addLast(j);
if (arr[qmax.getFirst()] - arr[qmin.getFirst()] > num) {
break;
}
j++;
}
if (qmin.peekFirst() == i) {
qmin.pollFirst();
}
if (qmax.peekFirst() == i) {
qmax.pollFirst();
}
res += j - i;
i++;
}
return res;
}
// for test
public static int[] getRandomArray(int len) {
if (len < 0) {
return null;
}
int[] arr = new int[len];
for (int i = 0; i < len; i++) {
arr[i] = (int) (Math.random() * 10);
}
return arr;
}
// for test
public static void printArray(int[] arr) {
if (arr != null) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int[] arr = getRandomArray(30);
int num = 5;
printArray(arr);
System.out.println(getNum(arr, num));
}
}
二、单调栈结构及其扩展面试题目
介绍单调栈结构
单调递增或单调递减的栈,跟单调队列差不多,但是只用到它的一端。
单调栈是一种特殊的栈,特殊之处在于栈内的元素都保持一个单调性。
单调栈的功能:
利用单调栈,可以找到从左/右遍历第一个比它小/大的元素的位置。
举个例子:
假设有一个单调递增的栈 S和一组数列:
a : 5 3 7 4
用数组L[i] 表示 第i个数向左遍历的第一个比它小的元素的位置
如何求L[i]?
首先我们考虑一个朴素的算法,可以按顺序枚举每一个数,然后再依此向左遍历。
但是当数列单调递减时,复杂度是严格的O(n^2)。
此时我们便可以利用单调栈在O(n)的复杂度下实现
我们按顺序遍历数组,然后构造一个单调递增栈
(1). i = 1时,因栈为空,L[1] = 0,此时再将第一个元素的位置下标1存入栈中
此时栈中情况:
(2).i = 2时,因当前3小于栈顶元素对应的元素5,故将5弹出栈
此时栈为空
故L[2] = 0
然后将元素3对应的位置下标2存入栈中
此时栈中情况:
(3).i = 3时,因当前7大于栈顶元素对应的元素3,故
L[3] = S.top() = 2 (栈顶元素的值)
然后将元素7对应的下标3存入栈
此时栈中情况:
(4).i = 4时,为保持单调递增的性质,应将栈顶元素3弹出
此时 L[4] = S.top() = 2;
然后将元素4对应的下标3存入栈
此时栈中情况:
至此 算法结束
对应的结果:
a : 5 3 7 4
L : 0 0 2 2
总结:一个元素向左遍历的第一个比它小的数的位置就是将它插入单调栈时栈顶元素的值,若栈为空,则说明不存在这么一个数。然后将此元素的下标存入栈,就能类似迭代般地求解后面的元素
代码:
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class MonotonousStack {
public static int[][] getNearLessNoRepeat(int[] arr) {
int[][] res = new int[arr.length][2];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
int popIndex = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
res[popIndex][0] = leftLessIndex;
res[popIndex][1] = i;
}
stack.push(i);
}
while (!stack.isEmpty()) {
int popIndex = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
res[popIndex][0] = leftLessIndex;
res[popIndex][1] = -1;
}
return res;
}
public static int[][] getNearLess(int[] arr) {
int[][] res = new int[arr.length][2];
Stack<List<Integer>> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {
List<Integer> popIs = stack.pop();
// 取位于下面位置的列表中,最晚加入的那个
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(
stack.peek().size() - 1);
for (Integer popi : popIs) {
res[popi][0] = leftLessIndex;
res[popi][1] = i;
}
}
if (!stack.isEmpty() && arr[stack.peek().get(0)] == arr[i]) {
stack.peek().add(Integer.valueOf(i));
} else {
ArrayList<Integer> list = new ArrayList<>();
list.add(i);
stack.push(list);
}
}
while (!stack.isEmpty()) {
List<Integer> popIs = stack.pop();
// 取位于下面位置的列表中,最晚加入的那个
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(
stack.peek().size() - 1);
for (Integer popi : popIs) {
res[popi][0] = leftLessIndex;
res[popi][1] = -1;
}
}
return res;
}
// for test
public static int[] getRandomArrayNoRepeat(int size) {
int[] arr = new int[(int) (Math.random() * size) + 1];
for (int i = 0; i < arr.length; i++) {
arr[i] = i;
}
for (int i = 0; i < arr.length; i++) {
int swapIndex = (int) (Math.random() * arr.length);
int tmp = arr[swapIndex];
arr[swapIndex] = arr[i];
arr[i] = tmp;
}
return arr;
}
// for test
public static int[] getRandomArray(int size, int max) {
int[] arr = new int[(int) (Math.random() * size) + 1];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * max) - (int) (Math.random() * max);
}
return arr;
}
// for test
public static int[][] rightWay(int[] arr) {
int[][] res = new int[arr.length][2];
for (int i = 0; i < arr.length; i++) {
int leftLessIndex = -1;
int rightLessIndex = -1;
int cur = i - 1;
while (cur >= 0) {
if (arr[cur] < arr[i]) {
leftLessIndex = cur;
break;
}
cur--;
}
cur = i + 1;
while (cur < arr.length) {
if (arr[cur] < arr[i]) {
rightLessIndex = cur;
break;
}
cur++;
}
res[i][0] = leftLessIndex;
res[i][1] = rightLessIndex;
}
return res;
}
// for test
public static boolean isEqual(int[][] res1, int[][] res2) {
if (res1.length != res2.length) {
return false;
}
for (int i = 0; i < res1.length; i++) {
if (res1[i][0] != res2[i][0] || res1[i][1] != res2[i][1]) {
return false;
}
}
return true;
}
// for test
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int size = 10;
int max = 20;
int testTimes = 2000000;
for (int i = 0; i < testTimes; i++) {
int[] arr1 = getRandomArrayNoRepeat(size);
int[] arr2 = getRandomArray(size, max);
if (!isEqual(getNearLessNoRepeat(arr1), rightWay(arr1))) {
System.out.println("Oops!");
printArray(arr1);
break;
}
if (!isEqual(getNearLess(arr2), rightWay(arr2))) {
System.out.println("Oops!");
printArray(arr2);
break;
}
}
}
}
题目:构造数组的MaxTree
定义二叉树节点如下:
public class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}一个数组的MaxTree定义如下:
- 数组必须没有重复元素
- MaxTree是一棵二叉树,数组的每一个值对应一个二叉树节点
- 包括MaxTree树在内且在其中的每一棵子树上,值最大的节点都是树的头。
给定一个没有重复元素的数组arr,写出生成这个数组的MaxTree的函数,要求如果数组长度为N,则时间复杂度为O(N)、额外空间复杂度为O(N)。
思考:
举例说明如何在满足时间和空间复杂度的要求下生成MaxTree。
arr={3,4,5,1,2}
3的左边第一个比3大的数:无 3的右边第一个比3大的数:4
4的左边第一个比4大的数:无 4的右边第一个比4大的数:5
5的左边第一个比5大的数:无 5的右边第一个比5大的数:无
1的左边第一个比1大的数:5 1的右边第一个比1大的数:2
2的左边第一个比2大的数:5 2的右边第一个比2大的数:无
以下列原则来建立这棵树:
- 每一个数的父结点是它左边第一个比它大的数和它右边第一个比它大的数中,较小的那个
- 如果一个数左边没有比它大的数,右边也没有。也就是说,这个数是整个数组的最大值,那么这个数就是MaxTree的头节点
那么3,4,5,1,2的MaxTree如下:
为什么通过这个方法能够正确地生成MaxTree呢?现给出证明:
- 通过这个方法,所有的数能够生成一棵树,这棵树可能不是二叉树,但肯定是一棵树,而不是多棵树(森林)。在数组中的所有数都不同,而一个较小的数肯定会以一个比自己大的数作为父节点,那么最终所有的数向上找都会找到数组中的最大值,所以它们会有一个共同的头。
- 通过这个方法,所有的数最多只有两个孩子。也就是说,这棵树可以用二叉树表示,而不需要多叉数。
如何尽可能快地找到每一个数左右两边第一个比它大的数呢?利用栈。找每个数左边第一个比它大的数,从左到右遍历每个数,栈中保持递减序列,新来的数不停地利用Pop出栈顶,直到栈顶比新数大或没有数。同样的方法可以求得每个数往右第一个比它大的数。
代码:
import java.util.HashMap;
import java.util.Stack;
/**
* 构造数组的MaxTree
*/
public class MaxTree {
private static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
private static Node getMaxTree(int[] arr) {
Node[] nArr = new Node[arr.length];
for (int i = 0; i != arr.length; i++) {
nArr[i] = new Node(arr[i]);
}
Stack<Node> stack = new Stack<Node>();
HashMap<Node, Node> lBigMap = new HashMap<Node, Node>();
HashMap<Node, Node> rBigMap = new HashMap<Node, Node>();
for (int i = 0; i < nArr.length; i++) {
Node currNode = nArr[i];
while ((!stack.isEmpty()) && stack.peek().value < currNode.value) {
popStackSetMap(stack, lBigMap);
}
stack.push(currNode);
}
while (!stack.isEmpty()) {
popStackSetMap(stack, lBigMap);
}
for (int i = nArr.length - 1; i != -1; i--) {
Node currNode = nArr[i];
while ((!stack.isEmpty()) && stack.peek().value < currNode.value) {
popStackSetMap(stack, rBigMap);
}
stack.push(currNode);
}
while (!stack.isEmpty()) {
popStackSetMap(stack, rBigMap);
}
Node head = null;
for (int i = 0; i != nArr.length; i++) {
Node currNode = nArr[i];
Node left = lBigMap.get(currNode);
Node right = rBigMap.get(currNode);
if (left == null && right == null) {
head = currNode;
} else if (left == null) {
if (right.left == null) {
right.left = currNode;
} else {
right.right = currNode;
}
} else if (right == null) {
if (left.left == null) {
left.left = currNode;
} else {
left.right = currNode;
}
} else {
Node parent = left.value < right.value ? left : right;
if (parent.left == null) {
parent.left = currNode;
} else {
parent.right = currNode;
}
}
}
return head;
}
private static void popStackSetMap(Stack<Node> stack, HashMap<Node, Node> map) {
Node popNode = stack.pop();
if (stack.isEmpty()) {
map.put(popNode, null);
} else {
map.put(popNode, stack.peek());
}
}
private static void printPreOrder(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
printPreOrder(head.left);
printPreOrder(head.right);
}
private static void printInOrder(Node head) {
if (head == null) {
return;
}
printPreOrder(head.left);
System.out.print(head.value + " ");
printPreOrder(head.right);
}
public static void main(String[] args) {
int[] uniqueArr = {3, 4, 5, 1, 2};
Node head = getMaxTree(uniqueArr);
printPreOrder(head);
System.out.println();
printInOrder(head);
}
}
题目:求最大子矩阵的大小
题目描述:给定一个整型矩阵map,其中的值只有0和1两种,求其中全是1的所有矩形区域中,最大的矩形区域为1的数量
例如:
1 1 1 0
其中,最大的矩形区域有3个1,所以返回3
再如:
1 0 1 1
1 1 1 1
1 1 1 0
其中,最大的矩形区域有6个1,所以返回6
思考:如果矩阵的大小为O(N*M),则可以做到时间复杂度为O(n*m)。具体过程如下:
- 矩阵的行数为N,以每一行做切割,统计以当前行作为底的情况下,每个位置往上的1的数量。使用高度数组height来表示。
- 对于每一次切割,都利用更新后的height数组来求出以每一行为底的情况下,最大的矩形是什么。那么这么多次切割中,最大的那个矩形就是我们要的。
核心思想:即在一个大的直方图中求最大矩形的面积。如果我们能够求出以每一根柱子扩展出去的最大矩形,那么其中最大的矩形就是我们想找的。考察每一根柱子最大能扩多大,这个行为的实质就是找到柱子左边刚比它小的柱子位置在哪里,以及右边刚比它小的柱子位置在哪里。这个过程怎么计算最快呢?用栈。
在遍历过程中有两个关键逻辑:
- 只有当前i位置的值height[i]大于当前栈顶位置所代表的值(height[stack.peek()]),则i位置才可以压入stack。所以stack中从栈顶到栈底的位置所代表的值是依次递减的,并且无重复值。
- 如果当前i位置的值height[i]小于或等于当前栈顶位置所代表的值(height[stack.peek()]),则把栈中存的位置不断弹出,直到某一个栈顶所代表的的值小于height[i],再把位置i压入,并在这期间做如下处理:
- 假设当前弹出的栈顶位置记为位置j,弹出栈顶之后,新的栈顶记为k。然后我们开始考虑位置j的柱子向右和向左最远能扩到哪里。
- 对于位置j的柱子来说,向右最远能扩到哪里呢?
- 如果height[j]>height[i],那么i-1位置就是向右能扩到的最远位置。因为j之所以被弹出,就是应为遇到了第一个比位置j值小的位置。
- 如果height[j]==height[i],那么i-1位置不一定是向右能扩到的最远位置,只是起码能扩到的位置,那怎么办呢?可以肯定的是,在这种情况下,i位置的柱子向左必然也可以扩到j位置。也就是说,j位置的柱子扩出来的最大矩形和i位置的柱子扩出来的最大矩形是同一个。所以,此时可以不再计算j位置的柱子能扩出来的最大矩形,因为位置i肯定要压入到栈中,那就等位置i弹出的时候再说。
- 对未知j的柱子来说,向左最远能扩到哪里呢?肯定是k+1位置。首先,height[k+1....j-1]之间不可能有小于或等于height[k]的值,否则k位置早从栈里弹出了。然后因为在栈里k位置和j位置原本是相邻的,并且从栈顶到栈底的位置所代表的值是依次递减并且无重复值,所以在height[k+1....j-1]之间不可能有大于或等于height[k],同时又小于或等于height[j]的,因为如果有这样的值,k和j在栈中就不可能相邻。所以height[k+1.....j-1]之间的值必然是既大于height[k],又大于height[j]的,所以j位置的柱子向左最远可以扩到k+1位置。
- 综上所述,j位置的柱子能扩出来的最大矩形为(i-k-1)*height[j]。
任何一个位置都仅仅进出栈1次,所以时间复杂度为O(M),既然每做一次切割处理的时间复杂度为O(M),一共做N次,则总的时间复杂度为O(N*M)。
代码如下:
import java.util.Stack;
public class MaximalRectangle {
public static int maxRecSize(int[][] map) {
if (map == null || map.length == 0 || map[0].length == 0) {
return 0;
}
int maxArea = 0;
int[] height = new int[map[0].length];
for (int i = 0; i < map.length; i++) {//枚举以i行打底
for (int j = 0; j < map[0].length; j++) {//生成i行打底的直方图数组
height[j] = map[i][j] == 0 ? 0 : height[j] + 1;
}
maxArea = Math.max(maxRecFromBottom(height), maxArea);
}
return maxArea;
}
/**
* height 无负数,可能有重复值
*
* @param height
* @return
*/
private static int maxRecFromBottom(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int maxArea = 0;
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (i - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
stack.push(i);
}
while (!stack.isEmpty()) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (height.length - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
return maxArea;
}
public static void main(String[] args) {
int[][] map = {{1, 0, 1, 1}, {1, 1, 1, 1}, {1, 1, 1, 0}};
System.out.println(maxRecSize(map));
}
}
相关题目:小B负责首都的防卫工作。
首都处于一个四面环山的盆地中,周围的n个小山构成一个环,作为预警措施,小B计划在每个小山上设置一个观察哨,日夜不停的瞭望周围发生的情况。
一旦发生外敌入侵事件,山顶上的岗哨将点燃烽烟。
若两个岗哨所在的山峰之间的那些山峰,高度都不大于这两座山峰,且这两个山峰之间有相连通路,则岗哨可以观察到另一个山峰上的烽烟是否点燃。
由于小山处于环上,任意两个小山之间存在两个不同的连接通路。满足上述不遮挡的条件下,一座山峰上岗哨点燃的烽烟至少可以通过一条通路被另一端观察到。
对于任意相邻的岗哨,一端的岗哨一定可以发现一端点燃的烽烟。
小B设计的这种保卫方案的一个重要特性是能够观测到对方烽烟的岗哨对的数量,她希望你能够帮她解决这个问题。
输入
输入中有多组测试数据。每组测试数据的第一行为一个整数n(3<=n<=10^6),为首都周围的小山数量,第二行为n个整数,依次表示小山的高度h,(1<=h<=10^9)。
输出
对每组测试数据,在单独的一行中输出能相互观察到的岗哨的对数。
样例输入
5
1 2 4 5 3
样例输出
7
算法思想:
此题可以理解为在两个山峰之间的山峰都比两端低时,两端山峰就是一对,现在就是求有多少对?此题可以转为环形链表中,一个数求他左右两边离他最近且大于他的数。
(1,2)(1,3)(2,3)(2,4)(4,5)(3,4)(3,5)可以看出最高和次高可以组成一对,其他数据都能有两个相邻最大值,所以此问题通解(n-2)*2+1。
找出一个数左右最近的大于他的数,可以用单调栈实现。我们设定单调栈中,从栈顶到栈底依次变大。
假设有数 5 2 1 4 3 7
先放5,2小于5,放2,1小于2,放1,4大于1,则1弹出,1的弹出是由于4,所以4是1右边临近的大于他的数,2在1下面,所以2是1左面临近大于他的数。相同原理2弹出,4进,3进,7进时同理弹出3,4,5
左 右
1 2 4
2 5 4
3 4 7
4 5 7
5 null 7
7 null null
总对数=4*2+1。此算法复杂度可以达到O(n),遍历算法O(n^2)
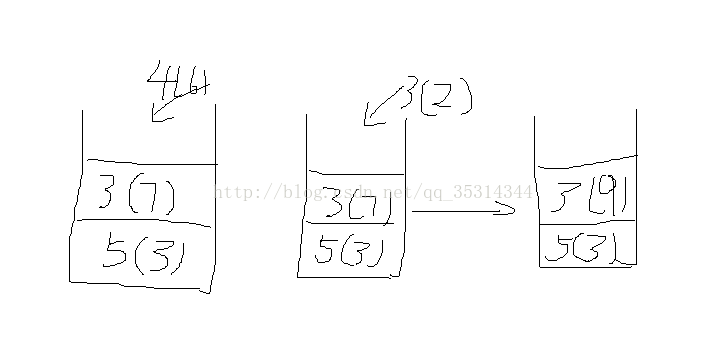
以上算法只适用于,山峰高度都各不相等的情况下,若有相等则:一次遍历将相邻相等山峰合并,二次遍历找最大值开始压栈
将3个5压入,7个3压入,当6个4压入时,7个3要出栈。7个3中,自己有对,与3相邻的4,可以看到每个3,所以有7对,5与4同理有7对,
共7*6/2+7+7。
当压入数据与栈顶数据相同,则只需合并个数即可。
没有数据入栈时,只需依次出栈,
纠正上图一个错误,对于7产生的个数,少加了一个12.因为只剩下7和10的时候,从10看向7和从7看向10是不一样的所以要加两次12
6是最后一个进栈的数,他要和栈底的数产生对数。
代码:
package NowCoder2.Class02;
import javafx.util.Pair;
import java.util.Scanner;
import java.util.Stack;
public class MountainsAndFlame {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
int size = in.nextInt();
int[] arr = new int[size];
for (int i = 0; i < size; i++) {
arr[i] = in.nextInt();
}
System.out.println(communications(arr));
}
in.close();
}
public static int nextIndex(int size, int i) {
return i < (size - 1) ? (i + 1) : 0;
}
//相邻相同山峰之间的对数,若只有一个,则没有成对,若有两个以上计算内部成对数
public static long getInternalSum(int n) {
return n == 1L ? 0L : (long) n * (long) (n - 1) / 2L;
}
public static class Pair {
public int value;
public int times;
public Pair(int value) {
this.value = value;
this.times = 1;
}
}
public static long communications(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int size = arr.length;
int maxIndex = 0;
for (int i = 0; i < size; i++) {
maxIndex = arr[maxIndex] < arr[i] ? i : maxIndex;//找到最高山峰的位置
}
int value = arr[maxIndex];//最高山峰的高度
int index = nextIndex(size, maxIndex);//最高山峰的下一个位置
long res = 0L;
Stack<Pair> stack = new Stack<Pair>();
stack.push(new Pair(value));
while (index != maxIndex) {
value = arr[index];
while (!stack.isEmpty() && stack.peek().value < value) {
int times = stack.pop().times;
// res += getInternalSum(times) + times;
// res += stack.isEmpty() ? 0 : times;
res += getInternalSum(times) + times * 2;//因为栈底是最大元素,所以在此阶段不可能跳出
}
if (!stack.isEmpty() && stack.peek().value == value) {
stack.peek().times++;
} else {
stack.push(new Pair(value));
}
index = nextIndex(size, index);
}
while (!stack.isEmpty()) {
int times = stack.pop().times;
res += getInternalSum(times);
if (!stack.isEmpty()) {
res += times;
if (stack.size() > 1) {//当栈底还剩大于1个的时候,弹出的那个数还可以与栈底的数成为对数
res += times;
} else {
res += stack.peek().times > 1 ? times : 0;
}
}
}
return res;
}
}