[Matlab科学计算] 1.你想要了解的欧拉角

[问题由来]

在计算铁磁材料多晶体的有效模量时，需要考虑晶粒在多晶体中的方向分布，一般用三个欧拉角（ $\psi ，\theta ，\phi$ , $\theta$ , $\phi$ ）来表示晶粒在多晶体中的方向，用方向分布函数 $W\left ( \psi ,\theta ,\phi \right )$ 来表示某个方向的分布密度。基于此，迫使我要掌握欧拉角，但是在阅读众多教材和博客文章中发现，大家对欧拉角的说法不是很统一，所以，基于我的理解整一下欧拉角的相关概念及使用注意事项。

一、几个概念

1.1经典欧拉角(Proper Euler angles)和泰勒布莱恩角(Tait-Bryan angles)

这两种欧拉角是按照旋转轴的顺序定义的，经典欧拉角是按照Z-X-Z，Y-X-Y，X-Y-X，Z-Y-Z，X-Z-X，Y-Z-Y这样的轴序旋转，即第一个旋转轴和最后一个旋转轴相同；而泰勒布莱恩角是按照X-Y-Z，Y-Z-X，Z-X-Y，X-Z-Y，Z-Y-X，Y-X-Z这样的轴序旋转，即每次旋转轴都不相同。

1.2内在旋转(intrinsic rotations)和外在旋转(extrinsic rotations)

这两个概念通过下图进行说明：即内在旋转每次旋转围绕的轴是上次旋转之后坐标系的某个轴，外在旋转每次旋转的轴是固定坐标系中的轴。

内在旋转与外在旋转的转换关系：互换第一次和第三次旋转的位置则两者结果相同。例如Z-Y-X旋转和内部旋转和X-Y-Z旋转的外部旋转的旋转矩阵相同。

1.3旋转矩阵（很重要）

主动旋转和被动旋转：主动旋转是指将向量或坐标系逆时针围绕旋转轴旋转，被动选是对坐标轴进行的逆时针旋转，相当于主动旋转的逆操作。

旋转矩阵有二维旋转和三维旋转，研究需要这里仅讨论三维旋转（被动旋转）。

假设OP为单位矢量且在XY平面内，则OP矢量在O-XYZ坐标系中坐标为 $\left ( cos\alpha ,sin\alpha ,0 \right )$ ，在新坐标系O-X’Y’Z’中的坐标为 $\left ( cos\left ( \alpha -\theta \right ),sin\left ( \alpha -\theta \right ),0 \right )$ ,展开之后为 $\left ( cos\alpha cos\theta +sin\alpha sin\theta ,sin\alpha cos\theta -cos\alpha sin\theta ,0 \right )$ ，写成矩阵的形式如下：

$\left [ \begin{matrix} x{}'\\ y{}'\\ z{}' \end{matrix} \right ]=\begin{bmatrix} cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0& 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z \end{bmatrix}$

将上式中的3*3的变换矩阵称为旋转矩阵。从Fig. 3中可以看出，被动旋转相当于将矢量OP绕Z轴主动顺时针旋转θ角。

同理，可以得到绕X轴和绕Y轴被动旋转的旋转矩阵，如下所示：

$R_x\left ( \theta \right )=\begin{bmatrix} 1 & 0& 0\\ 0& cos\theta & sin\theta \\ 0& -sin\theta & cos\theta \end{bmatrix}$ , $R_{y}\left ( \theta \right )=\begin{bmatrix} cos\theta & 0& -sin\theta \\ 0& 1& 0\\ sin\theta & 0 &cos\theta \end{bmatrix}$

相应的矢量绕坐标轴主动旋转的旋转矩阵如下所示：

$R_{z}\left ( \theta \right )=\begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta &0 \\ 0 & 0 &1 \end{bmatrix}$ , $R_{x}\left ( \theta \right )=\begin{bmatrix} 1 & 0& 0\\ 0& cos\theta & -sin\theta \\ 0& sin\theta & cos\theta \end{bmatrix}$ , $R_{y}\left ( \theta \right )=\begin{bmatrix} cos\theta & 0 & sin\theta \\ 0& 1 & 0\\ -sin\theta & 0 & cos\theta \end{bmatrix}$

二、举例计算

计算旋转矩阵一定要明确旋转顺序和旋转模式（内在旋转还是外在旋转，主动旋转还是被动旋转），由于内在旋转易于图解表达，通常使用内在旋转说明。如图4所示，旋转顺序为Z-X-Z的被动内在旋转。假设矢量OP在O-xyz坐标系中的坐标为OP0=（x, y, z）,在O-XYZ坐标系中的坐标为OP=（X, Y, Z）,分解计算步骤如下：

绕Z轴旋转之后的坐标为 $OP_{1}=R_{z}\left ( \alpha \right )\cdot OP_{0}$ ；
绕第一次旋转之后的X坐标旋转之后的坐标为 $OP_{2}=R_{x}\left ( \beta \right )\cdot OP_{1}$ ；
绕第二次旋转之后的Z坐标旋转之后的坐标为 $OP_{3}=R_{z}\left ( \gamma \right )\cdot OP_{2}$ ；

可以得到OP矢量在新坐标系中的坐标与在旧坐标系中的坐标之间的关系为 $OP=R_{z}\left ( \gamma \right )R_{x}\left ( \beta \right )R_{z}\left ( \alpha \right )\cdot OP_{0}$ ，所以总的旋转矩阵为 $T=R_{z}\left ( \gamma \right )R_{x}\left ( \beta \right )R_{z}\left ( \alpha \right )$ ，采用Matlab的符号计算可以得到该旋转矩阵的展开形式。为了便于Matlab中书写，令 $\alpha =a$ ， $\beta =b$ ， $\gamma =c$ 。

Matlab代码：

syms a b c
Rza = [cos(a) sin(a) 0;-sin(a) cos(a) 0;0 0 1];
Rxb = [1 0 0;0 cos(b) sin(b);0 -sin(b) cos(b)];
Rzc = [cos(c) sin(c) 0;-sin(c) cos(c) 0;0 0 1];
T = Rzc*Rxb*Rza;
disp(T);

计算结果：

[ cos(a)*cos(c) - cos(b)*sin(a)*sin(c), cos(c)*sin(a) + cos(a)*cos(b)*sin(c), sin(b)*sin(c)]
[-cos(a)*sin(c) - cos(b)*cos(c)*sin(a), cos(a)*cos(b)*cos(c) - sin(a)*sin(c), cos(c)*sin(b)] 
[               sin(a)*sin(b),                     -cos(a)*sin(b),                   cos(b)]

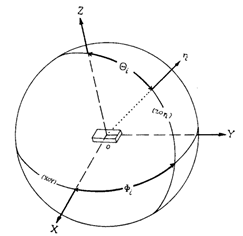
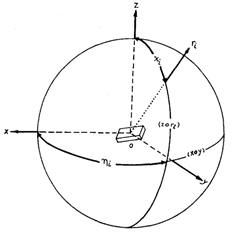
三、在晶体织构学中的应用

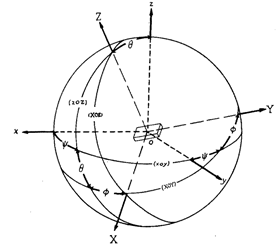
根据欧拉角 $\psi ,\theta ,\phi$ ，可以得到旋转矩阵为：

$T\left ( \psi ,\theta ,\phi \right )=R_{z}\left ( \phi \right )R_{y}\left ( \theta \right )R_{z}\left ( \psi \right ) =\begin{bmatrix} cos\psi cos\theta cos\phi -sin\psi sin\phi & sin\psi cos\theta cos\phi +cos\psi sin\phi & -sin\theta cos\phi \\ -cos\psi cos\theta sin\phi -sin\psi cos\phi & -sin\psi cos\theta sin\phi +cos\psi cos\phi &sin\theta sin\phi \\ cos\psi sin\theta & sin\psi sin\theta & cos\theta \end{bmatrix}$

根据旋转变换，则有如下公式：

$\begin{bmatrix} sin\Theta _{i}cos\Phi _{i}\\ sin\Theta _{i}sin\Phi _{i}\\ cos\Theta _{i} \end{bmatrix}=T\left ( \psi ,\theta ,\phi \right )\begin{bmatrix} sin\chi _{i}cos\eta _{i}\\ sin\chi _{i}sin\eta _{i}\\ cos\chi _{i} \end{bmatrix}$

进而，得到晶粒坐标系C中的矢量在试样坐标系S中的表达：

$\begin{bmatrix} sin\chi _{i}cos\eta _{i}\\ sin\chi _{i}sin\eta _{i}\\ cos\chi _{i} \end{bmatrix}=T^{-1}\left ( \psi ,\theta ,\phi \right )\begin{bmatrix} sin\Theta _{i}cos\Phi _{i}\\ sin\Theta _{i}sin\Phi _{i}\\ cos\Theta _{i} \end{bmatrix}$

假设所有晶粒在试样中的方向分布函数（ODF）为 $W\left ( \psi ,\theta ,\phi \right )$ ，而且有 $\int_{0}^{2\pi }\int_{0}^{\pi }\int_{0}^{2\pi }W\left ( \psi ,\theta ,\phi \right )sin\theta d\psi d\theta d\phi =1$ ，多晶体中常计算等效弹性刚度张量（四阶张量），所以得出，一个在试样坐标系S中的四阶张量 $\Omega _{mnpq}^{S}$ 能够从晶粒坐标系C中的 $\Omega _{mnpq}^{C}$ 计算得到，

$\Omega _{ijkl}^{S}=T_{im}T_{jn}T_{kp}T_{lq}\Omega _{mnpq}^{C}$

四阶张量 $\Omega$ 的体积平均变成取向平均，计算方法如下：

$\left \langle \Omega \right \rangle=\int_{0}^{2\pi }\int_{0}^{\pi }\int_{0}^{2\pi }\Omega ^{S}\left ( \psi ,\theta ,\phi \right )W\left ( \psi ,\theta ,\phi \right )sin\theta d\psi d\theta d\phi$