第九周学习笔记

1.论文阅读

Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines

作者：John C.Platt

时间： 1998年

主要内容：

1.文章解决了什么问题？

SVM训练算法在大规模问题上收敛很慢，且十分复杂、难以实现，运算过程中需要维持一个 $n^2$ 个元素的矩阵，当年(1998)，问题规模超过4000个样本时，就超过了当时的内存大小(128MB)。
曾经的训练算法之一的Chunking使得算法从维持 $n^2$ 个元素的矩阵降低到维持一个非0拉格朗日乘子数平方的元素数，但仍然无法解决大规模问题(内存不足)。
1997年Osuna提出了一个训练方法，并证明了解二次规划问题可以化归为解决其子问题，只要每次向子问题中增加一个违反KKT条件的样本即可。另一方面，为了让训练方法适应到任意规模的二次规划问题，Osuna在每次加入一个不满足KKT条件的样本同时，剔除一个样本以维持矩阵的大小恒定。存在的问题是每次为了一个样本运行整个二次规划数值算法，效率十分底下，而且会出现很多数值精度问题。

2.用了什么方法？

序列最小优化算法(SMO)，包括两个部分

一个解决两个拉格朗日乘子优化的分析方法
一个选择优化乘子的启发式方法。

3.效果如何

快，比chunking算法约快1阶
占用内存小，可以解决更大规模的问题
使用分析方法，不使用数值的二次规划方法
形式简单，容易实现
使用稀疏方法的加速效果显著

4.存在什么不足

需要更多的基准测试来使SMO成为一个标准的SVM训练方法。

5.其他

验证算法时需要注意的地方

保证对比算法是一个合适的benchmark
保证对比算法的代码实现与其公认的效率是符合的
保证两个算法的精度相同
保证两个算法解决的任务是合适的
使用了两个公开数据集和两个人工数据集，其中第一个人工数据集线性可分，另一个是噪音。
使用log-log图近似估计了算法的复杂度
仅选择了一组在验证集上表现较好的超参数

2.CS229

1.Problem Set#3

4.K-means
5.
( a ) $\begin{aligned} l(\theta^{(t+1)}) &\geq \sum_i\sum_{z^{(i)}}Q^{(t)}_i(z^{(i)})log\dfrac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q^{(t)}_i(z^{(i)})}\\ &\geq \sum_i\sum_{z^{(i)}}Q^{(t)}_i(z^{(i)})log\dfrac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q^{(t)}_i(z^{(i)})}\\ &=l(\theta^{(t)}) \end{aligned}$
第一个不等号根据琴生不等式成立，第二个不等号根据梯度下降成立
( b )因为琴生不等式等号条件满足，所以二者的更新法则一致。

3.实验，SMO算法的实现

代码在这
实验题目 SMO算法的实现
实验目的 深入理解SMO
实验过程
1.数据准备：Kaggle Titanic分类数据，891*6
2.SMO

main 算法运行主程序
func examinExample(i1) 检查第一个拉格朗日乘子，并选择第二个拉格朗日乘子的方法
func takeStep(i1,i2) 对两个拉格朗日乘子使用分析的方法进行二次规划

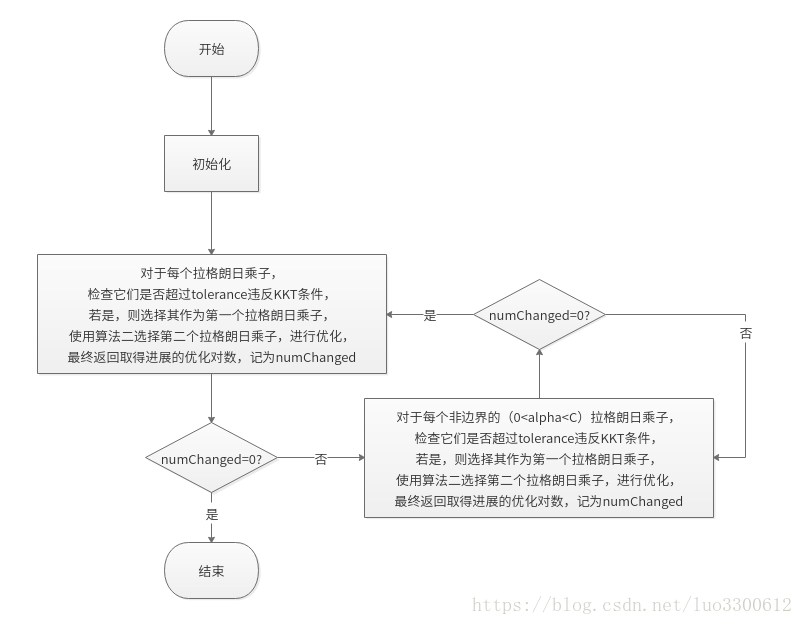
算法流程图如下所示
算法一，主步骤
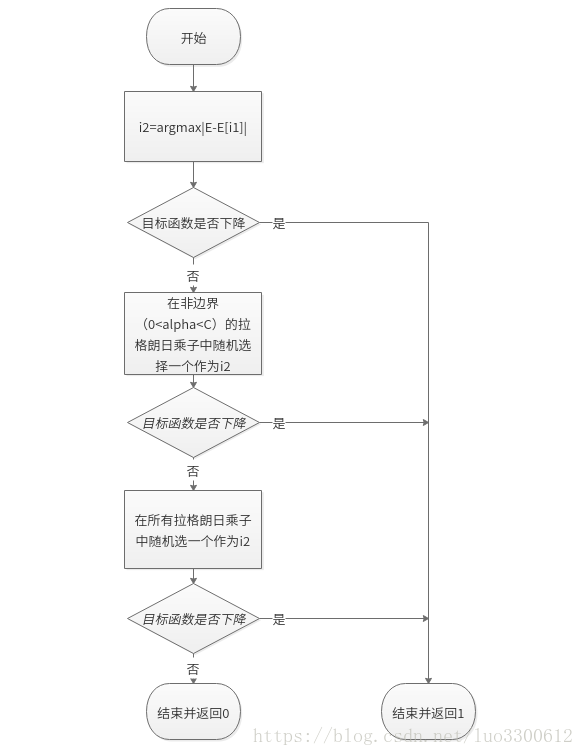
在这里插入图片描述
算法二，选定第二个拉格朗日乘子的方法

实验结果
取C=0.05（与论文中一致），十次运行取平均

样本数	50	100	150	200	250	300	350	400	450	500
耗时(s)	0.0	1.3	4.2	6.1	8.6	12.8	17.9	33.2	39.1	38.9
准确率	79.2%	78.4%	79.3%	78.5%	77.8%	79.5%	79.3%	79.2%	78.7%	78.9%
支持向量	4.1	10.7	18.8	30.6	41.7	56.8	68.7	88.1	107.8	130.1
非支持向量	45.9	139.3	281.2	469.4	708.3	993.2	1331.3	1711.9	2142.2	2619.9

实验结论
1.SMO算法相对而言易于实现。
2.支持向量只有一小部分
3.线性SVM和Logistic回归的效果相差不大