第八周PPT 下载密码:qedd
上周主要讲解了支持向量机SVM的原理包括优化目标、大间隔以及核函数等SVM核心内容,以及SVM的使用。本周主要讲解经典的无监督聚类算法k-means,包括k-means的优化目标,原理以及一些参数设置细节;和降维算法PCA的原理,目标,问题规划以及应用等问题。
目录
一、无监督学习
1.无监督学习
首先回顾一下之前的监督学习问题:
在监督学习问题中,每个训练样本都有一个标签,目标是用假设函数去拟合训练集,产生决策边界,对训练样本进行分类:

而在无监督学习问题中,训练样本没有任何标签信息。我们需要做的是把这些无标签的数据输入到算法中,利用算法找到这些数据中隐藏的结构。
对于下图中的数据,我们可以用算法找到一种隐藏结构-簇(这些数据可以分为两组分开的簇),我们称这个算法为聚类算法,这是我们学习的第一个无监督算法。当然无监督算法还有很多,可以发现数据中隐藏的不同结构,不仅仅是簇:

聚类的应用:

- 市场分割:对数据库中的顾客信息,根据市场进行分组,这样可以针对不同市场进行改进。
- 社交网络分析:找到关系密切的不同群体。
- 组织计算机集群
- 了解银河系的构成
2.K-Means算法
K-Means是目前使用最广泛的聚类算法。
- K-Means原理
第一步:可视化一组无标签训练集(,下图中的绿点),随机选择两个聚类中心(下图中的红、蓝叉):

第二步:遍历每个样本点,计算其与两个聚类中心的距离,离哪个聚类中心更近,就把该点划分为哪个聚类中心,一次遍历后如下所示:

第三步:移动聚类中心,分别对上图中的红、蓝色点计算均值,得到新的聚类中心:

重复第二、三步,直到聚类中心不在变化为止,得到的最终聚类效果如下:

- K-means算法输入

- K-means算法流程

其中第一个内循环是簇分配,;
第2个内循环是更新聚类中心(簇).比如,在第一个内循环结束后,有四个样本点被划分给了聚类中心
,即
,那么
.
如果某一个聚类中心没有分配到任何样本点时,一般是把这个聚类中心去除,此时K个聚类中心就变成了K-1个聚类中心;如果你的任务必须是把数据集分为K个簇,此时可以重新随机初始化K个聚类中心,重新开始。
- K-means也可以聚类没有明显簇结构的数据

之前接触到的数据集大多是左图这中,有明显的簇结构,使用K-means可以很显然的分为这三个簇;而也会有一些没有明显簇结构的数据,如右图所示,此时k-means也可以对其进行聚类。右图是一个T-shirt尺寸的数据集,它有身高和体重两个特征,使用k-means可能会分为如右图所示的三个簇,这样就可以根据聚类结果,设计不同类型的T-shirt。
3.优化目标
- 符号说明
:在最近的一次簇分配过程中,样本
被分配到的簇的聚类中心下标(离
最近的聚类中心的下标)
:某个聚类中心(k=1...K,
)
:样本
被分配到的簇的聚类中心(离
最近的聚类中心)
- 优化目标

实际上,K-means的算法流程,就是在实现这个优化目标:

第一个内循环-簇分配,固定聚类中心不动,关于变量
,最小化代价函数J;
第二个内循环-更新聚类中心,关于变量,最小化代价函数J;再进行下一次迭代。
4.随机初始化
本小节将介绍一种随机初始化聚类中心的方法,尽可能避免k-means陷入局部最优。
- 随机初始化
首先选择的聚类中心数K应该小于样本数m;
然后随机选择K个样本点作为初始的聚类中心,即
- 局部最优问题
随机初始化不同,k-means得到的聚类效果也是不同的,有时会陷入局部最优。局部最优指的是代价函数J得到一个局部最优解,考虑下图这种情况:

对于上图的这个样本集,最好的聚类效果应该如下图所示:

但是,可能由于随机初始化的不同,可能会得到下面的两种不同的聚类效果,这时我们称k-means算法陷入局部最优:

- 解决局部最优的方法
多次使用k-means算法,不同的随机初始化,会得到不同的聚类结果,对应不同的参数。从中找到一组最优的参数,是的代价函数J最小,那么该组参数所对应聚类结果认为是最好的:

这种方法在聚类中心数量K比较小(K=2-10,尤其是K=2-4时)时,效果比较好;当K比较大时,随机初始化对聚类结果的影响就没那么大了,此时这个方法的效果可能就不会很显著。
5.选择聚类数量
选择聚类中心的数量是一件非常困难的事情,不存在一种通用的自动选择算法,一般是通过人工或经验进行选择。
即使是对于能够可视化的数据,聚类中心数量的选择也是很模糊的,如下图所示:

上图中我们既可以选择左右两个聚类中心,也可以选择四个(左右又可以分为上下两部分),而且不同的选择间是没有对错的。
首先,先介绍一种自动选择聚类数量的算法:
- elbow method
这种自动选择算法,在某些情况下是有用的,原理大致如下图所示:

尝试不同的聚类数量,绘制代价函数J关于聚类数量K的曲线,如果曲线的形式类似于人的“胳膊”,那么在拐点(肘部)附近的聚类数量可以认为是最佳的选择。
但这种算法并非总是可行,有时可能会得到下图的这种曲线:

这种情况下,就很难选出合适的K。
一种更好的选择聚类数量的做法是:从聚类的目的出发,来选择K,评估在这种情况下的聚类效果是否能满足你的期望和将来的目的。
比如T-shirt型号的设计,如果你希望T-shirt有s,m,l三款,那么就可以对下图的身高、体重数据聚类时,让K=3:

如果你希望T-shirt有xs,s,m,l,xl五款,那么就可以对下图的身高、体重数据聚类时,让K=5:

具体选择K=3还是K=5,可以根据顾客需求以及营销状况来进一步决定。
二、降维
降维是另一种无监督学习算法。
1.目标I:数据压缩
数据压缩可以让数据占用更少的内存或硬盘空间,加速我们的学习算法。
首先看一个降维的例子:
如果一条数据有两个特征分别代表厘米长度和英寸长度,其实这两个特征是高度冗余的,完全可以把它压缩为一个长度特征,即把数据从2D->1D。

上图是上述数据集可视化的结果,他有两个特征,这些样本点大致分布在一条直线附近,我们可以把这些样本点投影到图中的那条蓝色的直线上,此时会得到一个新的数据集,他是原始数据集的一个近似;我们把这条直线抽出来,此时我们可以用一个特征就能定位所有的样本点,记这一个新特征为z。

接下来再看一个3D->2D的例子:
典型的降维例子一般是从1000D->100D这种类似的降维,但由于绘图的局限性,以3D->2D为例进行演示:
首先可视化原始数据集,他的每个样本有3个 特征:

这些样本点大致分布在一个平面上,我们可以把这些样本点都投影到这个平面上,得到一个新的数据集,他是原始数据集的一个近似:

将这个平面抽取出来,投影得到的新样本点,可以用两个特征来进行定位,从而实现了数据从3D->2D的压缩:

2.目标II:可视化
降维的另一个应用是数据可视化,在机器学习问题中,特征的维数一般非常大,这种情况下可视化是非常困难的。我们一般把高维数据压缩为2维或3维来帮助我们可视化高维数据,从而对机器学习算法做出改进。
接下来看一个例子:

上图为不同国家的一些相关数据,这个数据包含50个特征,上图是其中的一部分特征,包括GDP,人均GDP,居民幸福指数,人均收入,人均寿命等信息。
接下来将数据从50D压缩为2D:

然后对压缩后的数据进行可视化,探讨一下新特征代表的物理意义:

新特征z1可能代表一个国家整体的水平(如GDP,国家经济规模,国家整体科技实力等),新特征z2可能代表一个国家的人均水平(人均GDP,居民幸福程度,人均寿命等)。右上方的点代表一些发达国家,如美国,整体和人均都很高;右下方的点代表一些发展中国家,如中国,整体很高,但人均很低....等等
3.主成分分析问题规划1
主成分分析算法PCA是目前最流行的降维算法。接下来我们将介绍一下该算法的原理:
注意在应用PCA之前,一定要进行特征缩放。假设我们有如下所示的一个数据集():

对该数据集用PCA进行降维,也就是找到一条直线(上图中的红线),将所有样本点投影到这条直线上,数据便从2D->1D;PCA算法要求原始样本点和投影后的样本点的距离(投影误差)平方和最小。
对比上图中的红线,接下来演示一个不好的投影:

如上图中的品红色直线,此时所有样本的投影误差会非常大,不满足PCA的要求。
- PCA的一般定义
压缩数据2D->1D:
找到一个向量,将所有样本点投影到该向量上,并使得投影误差最小:

压缩数据nD->kD:
找到k个向量,将所有样本点投影到由这k个向量构成的子空间中,并使得投影误差最小。
以3D->2D进行演示:此时需要找到两个向量,这两个向量构成一个平面,将所有样本点投影到该平面上,并使得投影误差最小:

- PCA不是线性回归
PCA和线性回归是完全不同的两种算法:
1)线性回归中有一个特殊的输出变量y,所有输入特征x都用来预测这个y;而在PCA中没有特殊特征,所有特征都是同等对待的。

3)线性回归中拟合直线的要求是最小化样本点和直线上点的竖直距离;PCA要求是最小化样本点和直线上点的投影距离。
4.主成分分析问题规划2
- 数据预处理
使用PCA之前一定要对数据进行均值标准化,使每个特征的取值范围相近:

(
)
- 回顾PCA算法原理

左图将数据从2D->1D,首先找到一个向量,将所有样本点
投影到向量
上,得到新样本点
,要求所有样本点的投影误差最小。原始样本点
有
两个特征,新样本点
只有
一个特征。
右图将数据从3D->2D,首先找到两个向量,将所有样本点
投影到向量
构成的平面上,得到新样本点
,要求所有样本点的投影误差最小。原始样本点
有
三个特征,新样本点
只有
两个特征。
- 如何找到向量
将数据从n维压缩到k维:
首先计算协方差矩阵:

向量化写法:
然后对协方差矩阵进行奇异值分解,调用svd:
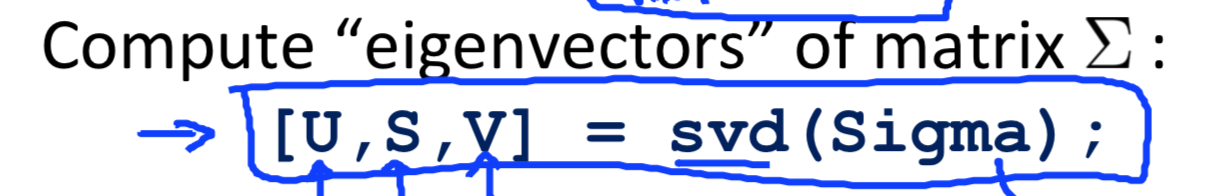
此时会返回3个矩阵,其中矩阵U是n*n的,它的每一列是,如果将n维数据降至k维,此时满足PCA要求的那k个向量就是矩阵U的前k列:

投影得到的新样本点

5.主成分数量选择
PCA主要是把数据从n维降至k维,本小节主要讲解参数k该如何选择:
投影误差平方均值:
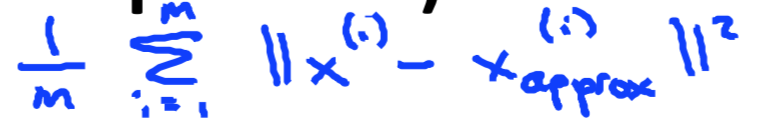
数据总方差:

选择k时,一般是从小往大取值(k=1,2,...),计算出相应的向量,看是否满足下图中的式子(意味着99%的方差被保留),若满足则取该K值。

有一个简单的做法,在调用svd时,除了返回第一个U矩阵,还会返回一个S矩阵(n*n),S矩阵是一个对角阵:

此时只需要检查下图中的式子成立就好了,他和之前检查的式子是等价的:

总结:
在对协方差矩阵进行svd分解后,从小到大尝试K值,直到满足上式,就取该K值;然后再取U矩阵的前k列,得到Ureduce,进而得到从原始样本x得到新样本z,完成从n维到k维的降维。
6.压缩重现
PCA可以把n维数据压缩为k维数据,相应地也可以通过一些犯法从k维数据得到原来n维数据的一个近似表示:
PCA:
逆过程:

7.应用PCA的建议
PCA可以加速学习算法的训练。
- 加速监督学习算法的训练
假设你有一个如下所示的训练集,并且输入特征的维数非常高,比如:
此时,如果直接直接对原始数据集进行训练的话,速度会很慢,可以尝试一下步骤:
第一步:提取原始数据集的输入特征,得到一个无标签的数据集,可能还需要对特征进行均值标准化,再对这个无标签的数据集进行PCA降维:

第二步:利用降维后的数据,构建新的训练集

在进行验证或测试时,对验证集和测试集进行同样的映射,在带入训练好的模型,计算精度。这样可以加快我们的训练速度。
- PCA的应用
1)压缩:减小存储数据所需要的内存和硬盘空间;加速学习算法的训练
2)可视化:可以把高维数据压缩到2D或3D进行可视化
- PCA糟糕的应用
1)利用PCA防止过拟合:

使用PCA在满足方差保留要求的前提下,可能会取得一个不错的效果,但是更好的防止过拟合的方法是正则化,所以不建议使用PCA防止过拟合。
- 盲目使用PCA加速学习算法
有时直接对原始训练集进行训练,是没有问题的,没必要一开始就考虑PCA来加速训练。
只有在用原始数据训练确实很慢,原始数据的存储代价很高或使用原始数据训练达不到你的要求时,再考虑使用PCA来加速训练。
三、实验