虽然写这个博客主要目的是为了给我自己做一个思路记忆录,但是如果你恰好点了进来,那么先对你说一声欢迎。我并不是什么大触,只是一个菜菜的学生,如果您发现了什么错误或者您对于某些地方有更好的意见,非常欢迎您的斧正!
动态规划(dynamic programming)与分治方法相似共同点:通过组合子问题的解来求解原问题的解。
不同点:分治方法求解互不相交的子问题,动态规划应用于子问题重叠的情况。
动态规划相对于分治算法的优点:分治算法每次求解一个子问题都重新计算,动态规划对每个子问题只求解一次(避免了重叠带来的消耗)。
动态规划通常用来求解最优化问题。

15.1钢条切割
问题描述:切割一根钢条,不同的长度对应不同的售价,如何切割使得获得最大的利益。

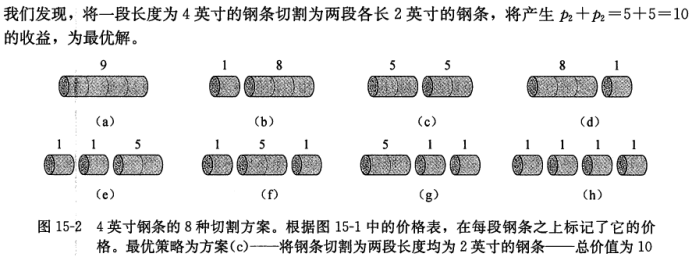
我们观察一下所有的最优收益值:
 第一个参数pn对应不切割
第一个参数pn对应不切割
由此最优解的形式为,pi为第一段的长度,r(n-i)则对应剩下的n-i的长度的最优切割方法:
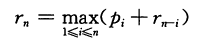
自顶向下递归实现
我们看一下自顶向下的伪代码
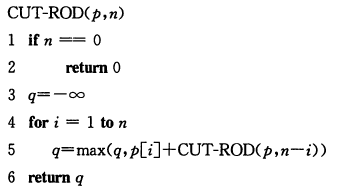
当钢条足够场的时候,这个解法就会很费时,比如当n=4:

也就是说,对于长度为n的钢条,它考察了2n-1 种可能的方案
使用动态规划方法求解最优钢条切割问题

朴素递归算法效率低下的原因:反复求解相同的子问题。
解决方法:对每个子问题求解一次,保存结果,下次再求解相同问题的时候,只需要查找该结果,是典型的时空权衡的例子。
动态规划有两种等价的实现方法:带备忘的自顶向下法 和 仔自底向上法
带备忘的自顶向下法:

自底向上法:

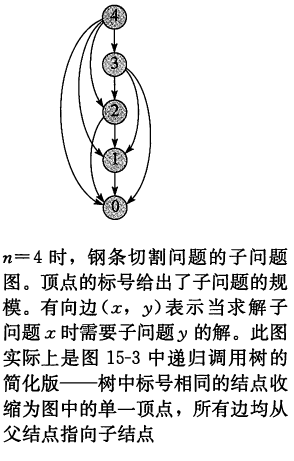
子问题图
每个顶点表示一个子问题。若求解子问题x的时候需要用到子问题y的解,就会有一条从x到y的有向边。
子问题图G=(V,E)的规模可以帮我们确定订台规划算法的运行时间。
重构解
前面给出的动态规划算法返回最优解的收益值,但并未返回解本身,我们另外创建一个数组记录每次切割的长度然后输出它就可以了。

15.2矩阵链乘法
首先我们回顾一下矩阵相乘的过程:

把这个过程写成伪代码:

假设我现在有三个矩阵A[10][100]、B[100][5]、C[5][50],要计算A·B·C,就会有(A·B)·C与A·(B·C)两种方式。
第一种:A·B 乘法次数:10x100x5=5000 变成一个[10][5]的矩阵
(A·B)·C 10x5x50=2500
一共需要5000+2500=7500次
第二种:B·C乘法次数:100x5x50=25000
A·(B·C) 10x100x50=50000
一共需要25000+50000=75000次
现在开始看一下我们要面对的问题:

计算括号化方案的数量
令P(n)表示可供选择的括号化方案,则:

通过暴力搜索穷尽所有可能的括号化方案来寻找最优方案,显然非常的糟糕。
应用动态规划方法
开头就已经列出了动态规划的步骤,我们再看一遍:

步骤1:最优括号方案的结构特征
也就是寻找最优子结构。假设A(i)A(i+1)…A(j)的最优括号化方案的分割点在A(k)和A(k+1)之间。那么继续对“前缀”子链A(i)A(i+1)…A(k)进行独立求解。我们必须保证在确定分割点的时候,已经考察了所有可能的划分点。
步骤2:一个递归求解方案
令m[i,j]表示计算矩阵A(i…j)所需标量乘法次数的最小值。

所以,递归求解公式为:
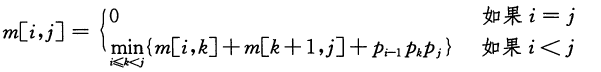
我们用s[i…j]保存最优分割点的位置k
步骤3:计算最优代价
我们采用自底向上表格法代替基于公式的递归算法来计算最优代价。为了实现自底向上方法,我们必须确定计算m[i,j]需要访问哪些其它表项。

运行过程:

步骤4:构造最优解


15.3动态规划原理
适合应用动态规划方法求解的最优化问题应该具备的要素:最优子结构和子问题重叠。
最优子结构
一个刻画子问题空间的好经验是:保持子问题空间尽可能简单,只在必要时才扩展它。
用子问题的总数和每个子问题需要考察多少种选择这两个因素的成绩来粗略分析动态规划算法的运行时间:
钢条切割:共有O(n)个子问题,每个子问题最多需要考察n种,因此运行时间为O(n^2)
矩阵链乘法:共有O(n2)个子问题,每个子问题最多需要考察n-1种,因此运行时间为O(n3)
用子问题图分析运行时间:
钢条切割:子问题图有O(n)个顶点,每个顶点最多n条边,运行时间为O(n^2)
矩阵链乘法:子问题图有O(n2)个顶点,每个顶点最多n-1条边,运行时间为O(n3)
一些微妙之处
注意问题是否具有最优子结构:给定一个有向图G=(V,E)和两个顶点u,v∈V
无权最短路径:找到一条从u到v的边数最少的路径。如果路径中包含环,将环去掉显然会减少边的数量。
无权最长路径:找到一条从u到v的边数最多的路径。如果路径中包含环,绕环不停走可以得到任意长的路径。
重叠子问题
对每个子问题只求解一次,而不是在递归的过程中重复求解。
重构最优解
我们通常用一个表,来保存我们已经求解的子问题,当要再次用到这个子问题的解的时候,只需要访问这个表就可以了,而不用继续递归求子问题的解。
备忘
就是上面提到的那个保存解的表。
15.4最长公共子序列

步骤1:刻画最长公共子序列的特征
暴力解法:穷举所有X的子序列,检查是否也是Y的子序列,记录找到的最长子序列。X共有2^n个子序列,这样的做法是不实用的!
现有X={A,B,C,B,A,C,B},定义A4={A,B,C,B},X0是空串,则:

如果有看不懂的话,可以自己写两个序列测试一下。
步骤2:一个递归解

步骤3:计算LCS的长度

修正一下:上图应该先遍历行再遍历列
再对上图进行一下说明:“↑”表示判断的时候,这个位置的值取上方的值,也就是情况3,“←”表示判断的时候,这个位置的值取左边的值,也就是else的情况,“↖”表示判断的时候,这个位置的值取左上方的值+1,也就是情况2。加一是因为最长公共子序列又增长了一位,c[i,j]表示的是从c[0,0]到c[i,j]这个大方框里已经有的最长公共子序列。
还有什么看不懂的可以在评论区与我交流。
假设 X=<A,B,C,B,D,A,B>
Y=<B,D,C,A,B,A>

步骤4:构造LCS
当遇到“↖”的时候,表示遇到了一个最长公共子序列的字母,只需按这个一路追踪即可,如上图的阴影部分。

15.5最优二叉搜索树
问题描述:给定一个n个不同关键字的已经排列的序列K,假设K中每个排列被搜索的概率已知,现在要求一棵二叉树的摆放方法,使得每个排列的概率x(每个排列的深度+1的和最小。比如根的概率为0.8,叶的概率为0.2,那么它合计为0.8x1+0.2x2=1.2,如果倒过来,就使0.2x1+0.8x2=1.8>1.2,显然第一种是最优解。
步骤1:最优二叉搜索树的结构
叶节点必然是伪关键字(概率非常小的那种)。
步骤2:一个递归算法
关键字的概率为q,伪关键字的概率为p。

最终递归公式:
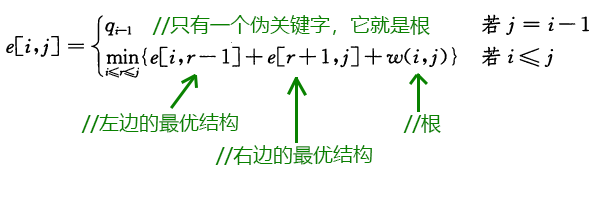
步骤三:计算最优二叉搜索树的期望搜索代价
为了避免每次计算e[i,j]的时候都重新计算w[i,j]我们把这些值保存在w[1…n+1,0…n]中

以下是代码部分,建议复制到自己的编辑器中运行一下:
动态规划_钢条切割.h
#pragma once
/*切割函数*/
void BottonUpCut(int p[], int n, int r[], int s[]);
/*测试函数*/
void TestCut();
动态规划_钢条切割.cpp
#include "动态规划_钢条切割.h"
#include <stdio.h>
#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;
/*切割函数*/
void BottonUpCut(int p[], int n,int r[],int s[])
{
r[0] = 0;
for (int j = 1; j <= n; j++)
{
int q = -1;
for (int i = 1; i <= j; i++)
{
/*我后来发现如果我的钢条太长的话p[i-1]是取不到值的,
所以这里跟书中有一点出入,不过这样就可以保证我们输入大值的时候不会出错!*/
if (q < p[(i-1)%10] + r[j - i])
{
q = p[(i - 1) % 10] + r[j - i];
s[j] = i;
}
}
r[j] = q;
}
}
void TestCut()
{
int n;
cout << "请输入钢条的长度:";
cin >> n;
int* r = new int[n + 1];/*收益数组*/
int* s = new int[n + 1];/*保存每次切割的长度*/
int p[10] = { 1,5,8,9,10,17,17,20,24,30};
cout << "最大的收益为:";
BottonUpCut(p, n, r, s);
cout << r[n]<<endl;
cout << "切割方法为:";
while (n > 0)
{
cout << s[n] << " ";
n = n - s[n];
}
delete[] r;
delete[] s;
}
主函数
#include "动态规划_钢条切割.h"
#include <stdio.h>
int main()
{
TestCut();
getchar();
getchar();
return 0;
}
运行结果
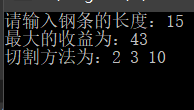
动态规划_矩阵链相乘.h
#pragma once
#include <vector>
#include <iostream>
using namespace std;
#define COUNT_ARRAY 7
/*矩阵链相乘*/
void ChainOrder(int p[],vector<vector<int>> &m, vector<vector<int>> &s);
/*构造最优解*/
void OptimalParens(vector<vector<int>> &s, int i, int j);
/*测试函数*/
void TestChainOrder();
动态规划_矩阵链相乘.cpp
#include "动态规划_矩阵链相乘.h"
#include <stdio.h>
#include <iostream>
#include <stdlib.h>
#include <time.h>
#include <vector>
using namespace std;
void ChainOrder(int p[], vector<vector<int>> &m, vector<vector<int>> &s)
{
int n = COUNT_ARRAY-1;
int i, j, k, L, q;
for (i = 1; i <= n; i++)
{
m[i][i] = 0;/*只有一个矩阵的情况*/
}
for (L = 2; L <= n; L++)
{
for (i = 1; i <= n - L + 1; i++)
{
j = i + L - 1;
m[i][j] = 200000;/*无穷大*/
for (k = i; k <= j - 1; k++)
{
q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (q < m[i][j])
{
m[i][j] = q;
s[i][j] = k;/*记录分割点*/
}
}
}
}
}
/*构造最优解*/
void OptimalParens(vector<vector<int>> &s, int i, int j)
{
if (i == j)
cout << "A"<<i;
else
{
cout<<"(";
OptimalParens(s, i, s[i][j]);
OptimalParens(s, s[i][j] + 1, j);
cout << ")";
}
}
/*测试函数*/
void TestChainOrder()
{
int p[COUNT_ARRAY] = {30,35,15,5,10,20,25};
vector< vector<int> > m;
vector< vector<int> > s;
m= vector<vector<int> >(COUNT_ARRAY, vector<int>(COUNT_ARRAY, 200000));
s= vector<vector<int> >(COUNT_ARRAY, vector<int>(COUNT_ARRAY, 200000));
ChainOrder(p,m,s);
cout << "最小的标量乘法次数为:" << m[1][6] << endl;
OptimalParens(s, 1, 6);
}
主函数
#include "动态规划_矩阵链相乘.h"
#include <stdio.h>
int main()
{
TestChainOrder();
getchar();
getchar();
return 0;
}
运行结果

动态规划_LCS.h
#pragma once
#include <vector>
#include <iostream>
using namespace std;
template<class T>
/*返回数组的长度*/
int SizeofChar(T& a);
/*求最长公共子序列*/
void LCS_Length(char X[], char Y[], vector<vector<int>> &b, vector<vector<int>> &c, int m, int n);
/*打印最长公共子序列*/
void PrintLCS(vector<vector<int>> &b, char X[], int i, int j);
/*测试函数*/
void TestLCS();
动态规划_LCS.cpp
#include "动态规划_LCS.h"
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
template<class T>
/*返回数组的长度*/
int SizeofChar(T& a)
{
return sizeof(a) / sizeof(a[0]);
}
/*求最长公共子序列*/
void LCS_Length(char X[], char Y[], vector<vector<int>> &b, vector<vector<int>> &c,int m,int n)
{
int i, j;
for (i = 1; i <= m; i++)/*初始化*/
c[i][0] = 0;
for (j = 0; j <= n; j++)
c[0][j] = 0;
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
if (X[i-1] == Y[j-1])/*从1开始的。*/
{
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = '↖';
}
else if (c[i - 1][j] >= c[i][j - 1])
{
c[i][j] = c[i - 1][j];
b[i][j] = '↑';
}
else
{
c[i][j] = c[i][j - 1];
b[i][j] = '←';
}
}
}
}
/*打印最长公共子序列*/
void PrintLCS(vector<vector<int>> &b, char X[], int i, int j)
{
if (i == 0 || j == 0)
return;
if (b[i][j] == '↖')
{
PrintLCS(b, X, i - 1, j - 1);
cout << X[i-1];
}
else if (b[i][j] == '↑')
PrintLCS(b, X, i - 1, j);
else
PrintLCS(b, X, i, j - 1);
}
/*测试函数*/
void TestLCS()
{
char X[8] = "ABCBDAB";
char Y[7] = "BDCABA";
vector<vector<int>> b = vector<vector<int> >(SizeofChar(X), vector<int>(SizeofChar(Y), 0));
vector<vector<int>> c = vector<vector<int> >(SizeofChar(X), vector<int>(SizeofChar(Y), 0));
int m = SizeofChar(X) - 1;
int n = SizeofChar(Y) - 1;
LCS_Length(X, Y, b, c, m, n);
cout << "LCS的长度为:" << c[m][n]<<endl;
PrintLCS(b, X, m, n);
}
主函数
#include "动态规划_LCS.h"
#include <stdio.h>
int main()
{
TestChainOrder();
getchar();
getchar();
return 0;
}
运行结果
