斐波那契数列介绍及Python中五种方法斐波那契数列

Q：斐波那契数列为什么那么重要，所有关于数学的书几乎都会提到？
A：因为斐波那契数列在数学和生活以及自然界中都非常有用。

在这里插入图片描述

1.　斐波那契数列概念引入

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”。

数学上，斐波那契数列以递归的形式进行定义：
$F_{0} = 0\\ F_{1} = 1\\ F_{n} = F_{n-1} + F_{n-2}$

场景

先来开看看“兔子数列”以及其他数学应用场景！！

1. 1　兔子数列

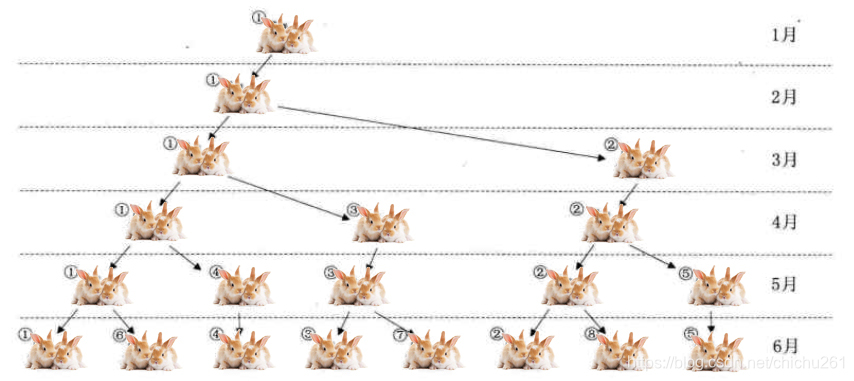
一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？

在这里插入图片描述

1.2　排列组合

有一段楼梯有10级台阶，规定每一步只能跨一级或两级，要登上第10级台阶有几种不同的走法?

更多数学方面知识，请戳：
斐波那契数列

斐波那契数列为什么那么重要，所有关于数学的书几乎都会提到？

…

2.　数列数学方法解答

2.1　兔子繁殖问题

斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”。

一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？

我们不妨拿新出生的一对小兔子分析一下：

第一个月小兔子没有繁殖能力，所以还是一对

两个月后，生下一对小兔对数共有两对

三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对

－－－－－－

依次类推可以列出下表：

经过月数	1	2	3	4	5	6	7	8	9	10	11	12	…
幼仔对数	1	0	1	1	2	3	5	8	13	21	34	55	…
成兔对数	0	1	1	2	3	5	8	13	21	34	55	89
总体对数	1	1	2	3	5	8	13	21	34	55	89	144

幼仔对数=前月成兔对数

成兔对数=前月成兔对数+前月幼仔对数

总体对数=本月成兔对数+本月幼仔对数

可以看出幼仔对数、成兔对数、总体对数都构成了一个数列。这个数列有关十分明显的特点，那是：

前面相邻两项之和，构成了后一项。

2.2　排列组合

2.2.1　跨楼梯组合

有一段楼梯有10级台阶，规定每一步只能跨一级或两级，要登上第10级台阶有几种不同的走法?

这就是一个斐波那契数列：登上第一级台阶有一种登法；登上两级台阶，有两种登法；登上三级台阶，有三种登法；登上四级台阶，有五种登法……

1，2，3，5，8，13……所以，登上十级，有89种走法。

2.2.2　掷硬币不连续情形

一枚均匀的硬币掷10次，问不连续出现正面的可能情形有多少种？

答案是:
$（1/√5)*{[(1+√5)/2]^(10+2) - [(1-√5)/2]^(10+2)}=144$
…

3.　Python代码实现斐波那契数列

时间复杂度

空间复杂度

通过时间复杂度和空间复杂度评判代码的执行效率。

例如：从规模上来说，如果需要计算F(4)的值，需要进行9次元素操作

设T(n)为计算n的时间复杂度，那么
$T(n) = T(n-1) + T(n-2)+O(1)$
一般情况，可以得出： $T(n)< 2* T(n-1) + O(1)$

粗略估算， $T（n） < O（2^n）$ ，上述代码求解F(n)的计算，它的时间复杂度是$O(2^n)

3.1　python特有写法

打印正整数n之内的斐波那契数列

# Python特有， 常规写法
def fib(self, n):
	a = 0
	b = 1
	while a <= n:
		print(a, end=" ", flush=True)
		a, b = b, a + b  # python不借助变量交换两数的值

fib(100)  # 求n之内的斐波那契数列

$时间复杂度：O(n)，空间复杂度：O(1)$

3.2　递归

打印斐波那契数列前10位数字

# 递归
def fibonacci(i):
    num_list = [0, 1]
    if i < 2:
        return num_list[i]
    elif i >= 2:
        return (fibonacci(i - 2) + fibonacci(i - 1))


print(fibonacci(10))

$时间复杂度：O(n)，空间复杂度：O(n)$

3.3　类对象

# 迭代的方式
class FibIterator(object):
    """斐波那契数列迭代器"""
    def __init__(self, n):
        """
        :param n: int, 指明生成数列的前n个数
        """
        self.n = n
        # current用来保存当前生成到数列中的第几个数了
        self.current = 0
        # num1用来保存前前一个数，初始值为数列中的第一个数0
        self.num1 = 0
        # num2用来保存前一个数，初始值为数列中的第二个数1
        self.num2 = 1

    def __next__(self):
        """被next()函数调用来获取下一个数"""
        if self.current < self.n:
            num = self.num1
            self.num1, self.num2 = self.num2, self.num1+self.num2
            self.current += 1
            return num
        else:
            raise StopIteration

    def __iter__(self):
        """迭代器的__iter__返回自身即可"""
        return self


if __name__ == '__main__':
    fib = FibIterator(10)
    for num in fib:
        print(num, end=" ")

3.4 矩阵解决问题

从定义开始：
$F_{0} = 0\\ F_{1} = 1\\ F_{n} = F_{n-1} + F_{n-2}$
转化为矩阵形式
$\begin{pmatrix} F_{n+1}\\ F_{n} \end{pmatrix}= \begin{pmatrix} 1&1\\ 1&0 \end{pmatrix}* \begin{pmatrix} F_{n}\\ F_{n-1} \end{pmatrix}$
可以得出： $\begin{pmatrix} F_{n+1}\\ F_{n} \end{pmatrix}\begin{pmatrix} 1&1\\ 1&0 \end{pmatrix}\begin{pmatrix} F_{1}\\ F_{0} \end{pmatrix}$
我们设定
$A=\begin{pmatrix} 1&1\\ 1&0 \end{pmatrix}$
很显然可以变为如下：
$A=\begin{pmatrix} F_{2}&F_{1}\\ F_{1}&F_{0} \end{pmatrix}$
通过数学归纳法可以推出以下公式：
$A^{n}=\begin{pmatrix} F_{n+1}&F_{n}\\ F_{n}&F_{n-1} \end{pmatrix}= \begin{pmatrix} 1&1\\ 1&0 \end{pmatrix}^{n}$
很显然计算F(n)的值，只需要进行矩阵的n次幂运算，取出结果矩阵第二行第一个元素值即可
$时间复杂度：O(n)，空间复杂度：O(1)$

这里可以利用快速幂运算求解，假设计算A的N次幂,二阶矩阵的乘法满足结合律

设A,B,C都是任意的二阶矩阵，则
$A(BC)=(AB)C$

我们设定： $m=[\frac{n}{2}]$

当n为偶数: $A^{N}=A^{m}∗A^{m}$
当n为奇数: $A^{N}=A^{m}∗A^{m}∗A$

相当于 $A^{6}=A^3∗A^3，A^7=A^3∗A^3∗A$

这样可以减少计算次数，因为 $A6=A∗A∗A∗A∗A∗A$ 这里有5个乘, $A6=（A∗A∗A）∗（A∗A∗A）$ 计算完 $A*A*A$ 得到结果 $A^3$ ，再乘以 $A^3$ 这里用了3个乘

以下是普通数据的快速幂运算，运算改为矩阵乘法,ret改为单位矩阵即可

def qpow(base, exp):
    if exp == 0:
        return 1
    ret = 1
    while exp:
        if exp & 1:
            ret = ret * base
        base = base * base
        exp >>= 1
    return ret

3.5 矩阵再推导

我们可以设定： $n=2m$
那么
$A^{2m}=\begin{pmatrix} F_{2m+1}&F_{2m}\\ F_{2m}&F_{2m-1} \end{pmatrix}=A^{m}*A^{m}$
已知
$A^{m}=\begin{pmatrix} F_{m+1}&F_{m}\\ F_{m}&F_{m-1} \end{pmatrix}$
所以：
$\begin{pmatrix} F_{m+1}&F_{m}\\ F_{m}&F_{m-1} \end{pmatrix}* \begin{pmatrix} F_{m+1}&F_{m}\\ F_{m}&F_{m-1} \end{pmatrix}= \begin{pmatrix} F_{2m+1}&F_{2m}\\ F_{2m}&F_{2m-1} \end{pmatrix}$
计算后可以得出：
$\begin{pmatrix} F_{2m+1}\\ F_{2m} \end{pmatrix}= \begin{pmatrix} F_{m+1}^{2}+F_{m}^{2}\\ F_{m}*(F_{m+1}+F_{m-1}) \end{pmatrix}$

这里需要注意一点 n 需要进行奇偶性判定：

当n为奇数时： $m=[\frac{n}{2}]，n=2*m+1$ 此时， $\begin{pmatrix} F_{n+1}\\ F_{n} \end{pmatrix}\begin{pmatrix} F_{2m+2}\\ F_{2m+1} \end{pmatrix}\begin{pmatrix} F_{m+1}*(F_{m+2}+F_{m})\\ F_{m+1}^{2}+F_{m}^{2} \end{pmatrix}$
由于 $F_{m+2}=F_{m+1}+F_{m}$ ，因此，可以推导出
$\begin{pmatrix} F_{n+1}\\ F_{n} \end{pmatrix}= \begin{pmatrix} F_{m+1}*(F_{m+1}+2*F_{m})\\ F_{m+1}^{2}+F_{m}^{2} \end{pmatrix}$
当n为偶数时： $m=\frac{n}{2}，n=2*m$ ，此时
$\begin{pmatrix} F_{n+1}\\ F_{n} \end{pmatrix}= \begin{pmatrix} F_{2m+1}\\ F_{2m} \end{pmatrix}= \begin{pmatrix} F_{m+1}^{2}+F_{m}^{2}\\ F_{m}*(F_{m+1}+F_{m-1}) \end{pmatrix}$
由于 $F_{m+2}=F_{m+1}+F_{m}$ ，因此，可以推导出：
$\begin{pmatrix} F_{n+1}\\ F_{n} \end{pmatrix}= \begin{pmatrix} F_{m+1}^{2}+F_{m}^{2}\\ F_{m}*(2*F_{m+1}-F_{m}) \end{pmatrix}$

所以计算F(N)的值，只需要知道F(n/2+1)和F(n/2)即可

def fib(n):
    if n < 1:
        return (1, 0)

    f_m_1, f_m = fib(n >> 1)
    if n & 1:
        return f_m_1 * (f_m_1 + 2 * f_m), f_m ** 2 + f_m_1 ** 2
    else:
        return f_m_1 ** 2 + f_m ** 2, f_m * (2 * f_m_1 - f_m)

$时间复杂度：O(\log_2 n)，空间复杂度：O(1)$