版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/Daycym/article/details/84337588
回顾
线性回归的损失函数为:
梯度下降法求解结果为:
上式为对于一个样本的对 梯度,在求梯度时,需要遍历每个
for j in range(样本特征数)
的更新公式为:
以上
基于梯度下降法的自线性模型
- 构建模型训练函数
fit()
fit(X, Y, alphas, threshold=1e-6, maxIter=200, addConstantItem=True)
参数:
- X:训练数据特征,X必须是List集合
- Y:训练数据标签,Y也必须是List集合
- alphas:学习率
- threshold:损失函数值小于此值停止迭代
- maxIter:迭代次数
- addConstantItem:是否有常数项
再调用模型训练函数后,我们需要对传入的训练数据进行校验,满足条件才能进行梯度计算以及参数的更新
- 1.校验数据
def validate(X, Y):
if len(X) != len(Y): # 特征数据与标签数据个数不一样
raise Exception("参数异常")
else:
m = len(X[0]) # 第一个样本的特征数目
for l in X: # 遍历所有样本
if len(l) != m: # 只要有一个样本的特征数目与第一个不一样
raise Exception("参数异常")
if len(Y[0]) != 1: # 不是单标签
raise Exception("参数异常")
- 2.计算 差异值
# x表示一个样本,y表示对应的标签,a表示theta值
def calcDiffe(x, y, a):
# 计算y - ax的值
lx = len(x) # 特征数目
la = len(a) # theta个数
if lx == la: # 相等的话就不包含常数项
result = 0
for i in range(lx):
result += x[i] * a[i] # 相乘求和
return y - result
elif lx + 1 == la: # 特征个数比theta多一个,表示有一个是常数项
result = 0
for i in range(lx):
result += x[i] * a[i]
result += 1 * a[lx] # 加上常数项
return y - result
else : # 否则参数异常
raise Exception("参数异常")
- 3.模型训练
def fit(X, Y, alphas, threshold=1e-6, maxIter=200, addConstantItem=True):
"""
X:训练数据特征,X必须是List集合
Y:训练数据标签,Y也必须是List集合
alphas:学习率可选范围
threshold:损失函数值小于此值停止迭代
maxIter:迭代次数
addConstantItem:是否有常数项
"""
# 数据校验
validate(X, Y)
# 开始模型构建
l = len(alphas) # 学习率的个数
m = len(Y) # 标签个数
n = len(X[0]) + 1 if addConstantItem else len(X[0]) # 样本特征的个数,如果有常数项就+1
# 模型的格式:控制最优模型
B = [True for i in range(l)]
# 差异性(损失值)
J = [np.nan for i in range(l)] # loss函数的值
# 1. 随机初始化theta值(全部为0), a的最后一列为常数项
a = [[0 for j in range(n)] for i in range(l)] # theta,是模型的系数,有len(alpha)组,分别记录每个学习率的模型系数
# 2. 开始计算
for times in range(maxIter): # 迭代次数
for i in range(l): # 选择学习率
if not B[i]:
# 如果当前alpha的值已经计算到最优解了,那么不进行继续计算
continue
# 梯度下降计算(计算所有数据)
ta = a[i] # 第i组theta值,与alpha对应
for j in range(n): # 遍历样本特征
alpha = alphas[i] # 选择学习率
ts = 0
for k in range(m): # 遍历所有样本
if j == n - 1 and addConstantItem: # 最后一个是常数项将公式中的x_j设为1
ts += alpha*calcDiffe(X[k], Y[k][0], a[i]) * 1
else: # 其他的theta更新公式后半部分按公式计算
ts += alpha*calcDiffe(X[k], Y[k][0], a[i]) * X[k][j]
t = ta[j] + ts # 更新theta
ta[j] = t # 记录新的theta
# 计算完一个alpha值的theta的损失函数
flag = True
js = 0
for k in range(m):
js += math.pow(calcDiffe(X[k], Y[k][0], a[i]),2) # 损失函数
if js > J[i]:
flag = False
break;
if flag:
J[i] = js
for j in range(n):
a[i][j] = ta[j] # 更新theta
else:
# 标记当前alpha的值不需要再计算了
B[i] = False
# 计算完一个迭代,当目标函数/损失函数值有一个小于threshold的结束循环
r = [0 for j in J if j <= threshold]
if len(r) > 0:
break
# 如果全部alphas的值都结算到最后解了,那么不进行继续计算
r = [0 for b in B if not b]
if len(r) > 0:
break
# 3. 获取最优的alphas的值以及对应的theta值
min_a = a[0]
min_j = J[0]
min_alpha = alphas[0]
for i in range(l):
if J[i] < min_j:
min_j = J[i]
min_a = a[i]
min_alpha = alphas[i]
print("最优的alpha值为:",min_alpha)
# 4. 返回最终的theta值
return min_a
- 预测结果与模型评估
# 预测结果
def predict(X,a):
Y = []
n = len(a) - 1
for x in X:
result = 0
for i in range(n):
result += x[i] * a[i]
result += a[n]
Y.append(result)
return Y
# 计算实际值和预测值之间的相关性
def calcRScore(y,py):
if len(y) != len(py):
raise Exception("参数异常")
avgy = np.average(y)
m = len(y)
rss = 0.0
tss = 0
for i in range(m):
rss += math.pow(y[i] - py[i], 2)
tss += math.pow(y[i] - avgy, 2)
r = 1.0 - 1.0 * rss / tss
return r
模型比较
至此,基于梯度下降法的自线性回归模型就构建好了,下面我们可以利用自模型进行训练,并与sklearn库中的线性回归模型进行对比,对比结果如下:
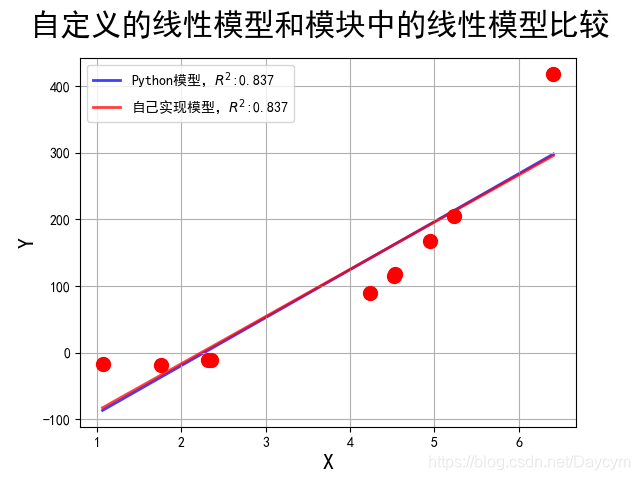
上图我们可以发现,自己实现的模型与python自带的模型的结果基本一致
源代码
Github下的08_基于梯度下降法的线性回归.py