1.8 谱聚类

1.绪论

在此篇文章中，对于谱聚类的解释基于图论，并不涉及Random walks（在参考的文章中（1）中有详细解释）

在叙述理论推导的同时，还需要给出简单的例子进行计算以加深理解。

给定一个带权无向图 $G=(V,E)$ , $V$ 是结点集合， $E$ 是边的集合。在谱聚类中，所有的样本构成了结点集合V，结点 $i,j$ 之间的相似度 $s_{i,j}$ 就是对应边的权重 $w_{i,j}$ 。聚类的目标就是将这些结点分成不同类，类与类之间有着较小的相似度，而类中的结点有着较大的相似度。这个目标在给定的相似度图 $G$ 中，就是对 $G$ 进行一个划分。一些相关定义如下：

(0).图论相关定义：无向带权图 $G=(V,E)$

对于V中的任意两个点，可以有边连接，也可以没有边连接。定义权重 $w_{i,j}$ 为点vi和点vj之间的权重。

由于是无向图，所以wij=wji，即邻接矩阵是对称的。对于有边连接的两个点vi和vj，wij>0,对于没有边连接的两个点vi和vj，wij=0。对于结点自身，wii=0。

对于图中的任意一个点vi，它的度 $d_i$ 定义为和它相连的所有边的权重之和，即 $d_i = \sum_{j=1}^{n}w_{i,j}$ 。

利用每个点度的定义，可以得到一个nxn的度矩阵D,它是一个对角矩阵，只有主对角线有值，对应第i行的第i个点的度数，定义为： $D=\begin{bmatrix} d_{1,1} &...& 0\\ ...& d_{i,i}& ...\\ 0& ... & d_{n,n} \end{bmatrix}$ 。

对于V中的一个子集A，定义A的补集 $\bar{A}=V\setminus A$ 。

$|A|=$ A中结点的个数。 $vol(A)=\sum_{i\in A} d_{i}$ 。指示向量： $\mathbf{1_A}=f=[f_1,f_2,...,f_n]^T\in R^n$ , $f_i=\left\{\begin{matrix} 0,v_i\in A\\ 1,v_i \notin A \end{matrix}\right.$ 。

(1) 相似矩阵的构建：在给出上述图论的标准定义后，有一个问题就是：邻接矩阵的构建时权重怎么得到？我们只能通过数据之间的关系得到，而不能手动输入。具体的做法就是：给定一个相似度函数去定量衡量。具体有三种：

a. $\epsilon$ 邻近法：给定一个阈值 $\epsilon$ ，欧式距离大于它，相似度为0；相似度小于它为 $\epsilon$ ，相似度为 $\epsilon$ 。

$W_{i,j}=\left\{\begin{matrix} 0,s_{i,j}< \epsilon \\ \epsilon,s_{i,j}\geq \epsilon \end{matrix}\right.$ ,很明显，这种方式相似度的衡量很不精确，因此在实际应用中，很少使用ϵ-邻近法。

b.K邻近法:利用KNN算法遍历所有的样本点，取每个样本最近的k个点作为近邻，只有和样本距离最近的k个点之间的wij>0

。但是这种方法会造成重构之后的邻接矩阵W非对称，而后面的算法一定需要对称邻接矩阵。

为了解决这种问题，一般采取下面两种方法：

c.全连接法：相比前两种方法，第三种方法所有的点之间的权重值都大于0，因此称之为全连接法。可以选择不同的核函数来定义边权重，常用的有多项式核函数，高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF，此时相似矩阵和邻接矩阵相同：

$W_{i,j}=exp(\frac{||x_i-x_j||^2}{2\sigma^2})$ 。

附加的两个点的就是：正如b中所讨论的，相似的衡量可能不是对称的但是必须保证每个元素非负，有一种再得到相似矩阵后，构造出对称的邻接矩阵方式是: $W = \frac{S+S^T}{2}$ 。此外，还要注意一点的是，正如c中所表示的，在谱聚类中，邻接矩阵的每两个结点都可能有相似度，它虽然很小，但不一定必须是0，这和图论中标准定义下的邻接矩阵有点区别：

有没有边连接导致对应的邻接矩阵元素是否必然为0。

（2）拉普拉斯矩阵：（标准定义：带权无向，权值非负）

拉普拉斯矩阵的定义： $L = D-W$ (D就是度矩阵，W就是邻接矩阵。

L的相关性质如下：

a.对于任意的向量 $x\in R^n$ , $x^TLx=x^TDx -x^TWx=\sum_{i=1}^{n}d_ix_i^2-\sum_{i,j=1}^{n}x_{i,j}w_{i,j}\\ =\frac{1}{2}(\sum_{i=1}^{n}d_ix_i^2-2\sum_{i,j=1}^{n}x_ix_jw_{i,j}+\sum_{j=1}^{n}d_jx_j^2)=\frac{1}{2}\sum_{i,j=1}^{n}w_{i,j}(x_i-x_j)^2$

公式太丑，看一个简单的例子：

假设我们有一个图（全连通），它的 $W=\begin{bmatrix} 0 &1 &2 \\ 1& 0&4 \\ 2& 4& 0 \end{bmatrix},D =\begin{bmatrix} 3 &0 &0 \\ 0& 5& 0\\ 0& 0& 6 \end{bmatrix}, L = \begin{bmatrix} 3 &-1 &-2 \\ -1& 5& -4\\ -2& -4& 6 \end{bmatrix}.$ ,

$x^TLx=[x_1,x_2,x_3]\begin{bmatrix} 3 &-1 &-2 \\ -1& 5& -4\\ -2& -4& 6 \end{bmatrix}\begin{pmatrix} x_1\\x_2 \\ x_3 \end{pmatrix}$ $=\frac{1}{2}(6x_1^2+10x_2^2+12x_3^2-4x_1x_2-8x_1x_3-16x_2x_3)$

因为W= $\begin{bmatrix} 0 &1 &2 \\ 1& 0&4 \\ 2& 4& 0 \end{bmatrix}$ ，右边 $=\frac{1}{2}(2(x_1-x_2)^2+4(x_1-x_3)^2+8(x_2-x_3)^2))$ $=\frac{1}{2}(2(x_1^2+x_2^2-2x_1x_2)+4(x_1^2+x_3^2-2x_1x_3)+8(x_2^2+x_3^2-2x_2x_3)))=\frac{1}{2}(6x_1^2+10x_2^2+12x_3^2-4x_1x_2-8x_1x_3-16x_2x_3)$

b.由a可知，L对称半正定，特征值是大于等于0的实数。

证明如下：记 $Lx=\lambda x,x^TLx=\lambda x^Tx$ ,当 $\lambda = 0,x^TLx=0$ 。

c.当L是全连通图时，特征值为0对应的特征向量是 $\mathbf{1_{n \times 1}}$ 。证明如下：

在b的基础上，由a的右边可知： $x_i=x_j$ ,利用之前指示向量的定义，令 $x_i=1$ 。

d.L中特征值为0的个数等于L中连通分量 $A_1,A_2,...,A_k$ 的个数，特征值为0的特征空间的基是： $\mathbf{1_A_1,1_A_2,...,1_A_k}$ 。

证明思路：1）当全连通时，特征向量是 $\mathbf{1}$ . 2)当有连通分量时，将L分块成每一块连通分量对应的拉普拉斯矩阵，然后证明即可。

总结就是：当L是图论标准定义下拉普拉斯矩阵时，它的0特征值个数表示有多少个连通分量，0所对应的特征指示向量说明了哪些结点在当前的连通分量中。

到这里，我们就已经可以完成聚类的目的了。对样本的聚类可以把它看成对样本所构成的图分成多个连通分支，用上述的方法，每一个类对应于一个连通分量。但是这种解释还是不鲁棒，因为在实际的谱聚类中，邻接矩阵（全联通）并不是完全对应于图论中的标准定义，所以有更深入的解释。

（3）切图方法:对于谱聚类更深入的分析

定义：对于任意两集合 $A,B\in V, A\cap B=\o$ ，定义A，B之间的切图权重： $W(A,B)=\sum_{i\in A ,j\in B} w_{i,j}$ 。

对于k个集合 $A_1,A_2,...A_k$ ,定义切图 $cut(A_1,A_2,...,A_k)=\frac{1}{2}\sum_{i\in A_i}^{k}W(A_i,\bar{A_i})$ 。一个例子：

我们的图如上图，则邻接矩阵为 $W=\begin{bmatrix}0 &1 & 4& 5& 0\\1 & 0& 0& 0&3 \\4 &0 &0 &6 &0 \\5 & 0&6 &0 &2 \\0 &3 &0 &2 & 0\end{bmatrix}$ ，记 $A_{1}=\begin{Bmatrix} v_1&v_3 &v_4 \end{Bmatrix},A_2=\begin{Bmatrix} v_2\end{Bmatrix},A_3=\begin{Bmatrix} v_5\end{Bmatrix}$ ,

所以切图 $cut(A_1,A_2,A_3)=\frac{1}{2}\sum_{i=1}^{3}W(A_i,\bar{A_i})= \frac{1}{2}(W(A_1,\bar{A_1})+W(A_2,\bar{A_2})+W(A_3,\bar{A_3}))$ ,

$W(A_1,\bar{A_1})=\sum_{i\in A_1 ,j\in \bar{A_1}} w_{i,j}=\sum_{i\in{1,3,4},j\in2,5} w_{i,j}$ ,就是矩阵 $\begin{bmatrix}0 &1^{\circ} & 4& 5& 0^{\circ}\\1 & 0& 0& 0&3 \\4 &0^{\circ} &0 &6 &0 ^{\circ}\\5 & 0^{\circ}&6 &0 &2^{\circ} \\0 &3 &0 &2 & 0\end{bmatrix}$ 中右上角标有圆圈的元素之和。

同理 $W(A_2,\bar{A_2})=\sum_{i\in A_2 ,j\in \bar{A_2}} w_{i,j}=\sum_{i\in{2},j\in 1,3,4,5} w_{i,j}$ ,对应的求和元素是 $\begin{bmatrix}0 &1 & 4& 5& 0\\1^{\circ} & 0& 0^{\circ}& 0^{\circ}&3 ^{\circ}\\4 &0 &0 &6 &0 \\5 & 0&6 &0 &2 \\0 &3 &0 &2 & 0\end{bmatrix}$ 中有圈的。

$W(A_3,\bar{A_3})=\sum_{i\in A_3 ,j\in \bar{A_3}} w_{i,j}=\sum_{i\in{3},j\in 1,2,4,5} w_{i,j}$ ，对应的求和元素是 $\begin{bmatrix}0 &1 & 4& 5& 0\\1 & 0& 0& 0&3 \\4^{\circ} &0^{\circ} &0 &6^{\circ} &0^{\circ} \\5 & 0&6 &0 &2 \\0 &3 &0 &2 & 0\end{bmatrix}$ 中有圈的。

如果聚类的目标是最小化切图函数 $cut(A_1,A_2,...,A_k)=\frac{1}{2}\sum_{i\in A_i}^{k}W(A_i,\bar{A_i})$ ，是有问题的？为什么呢？因为cut没有考虑子图的规模，比较直观的例子就是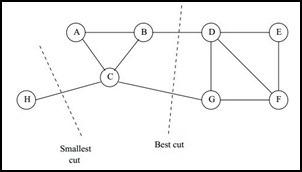：,smallest不是best.所以在考虑切图方法时，还需要考虑结点集合本身的规模（即本文开头所定义的 $|A_i| \ or \ vol(A_i)$ ）。根据所选用的不同的规模衡量函数，有RatioCut和Ncut两种切图方式。下面逐一介绍：

a.RatioCut:

RatioCut所考虑的最小划分函数是： $RatioCut(A_1,A_2,...,A_k)=\frac{1}{2}\sum_{i\in A_i}^{k}\frac{W(A_i,\bar{A_i})}{|A_i|}=\sum_{i=1}^{k}\frac{cut(A_i,\bar{A_i})}{|A_i|}$ ，

指示向量重新定义为：

$\mathbf{h_{j}}\in [\mathbf{h_1,h_2,...,h_k}]\in R^n \ and\ \mathbf{h_{i,j}}=\left\{\begin{matrix} \frac{1}{\sqrt{|A_i|}},v_j\in A_j\\0,v_j \notin A_j\end{matrix}\right.$ $i=1,2,...,n$ , $j=1,...,k$ $h_{i,j}$ 表示第j类的指示向量的第i个分量。

对于每一个h， $h_j^T Lh_j=\frac{1}{2}\sum_{a,b=1}^{n}w_{a,b}(h_{a,j}-h_{b,j})^2$ $=\frac{1}{2}\sum_{a\in A_j,b\notin A_j}w_{a,b}(\frac{1}{\sqrt|A_j|}-0)^2+\frac{1}{2}\sum_{a\in A_j,b\notin A_j}w_{a,b}(0-\frac{1}{\sqrt|A_j|})^2$

$=\frac{1}{2} (\frac{cut(A_j,\bar{A_j})}{|A_j|}+\frac{cut(\bar{A_j},A_j)}{|A_j|})=\frac{cut(A_j,\bar{A_j})}{|A_j|}$ 。

而对于所有的指示向量，有 $h_j^TLh_j=(H^TLH)_{jj}$ .

$RatioCut(A_1,A_2,...,A_k)=\sum_{j=1}^{k}h_j^TLh_j=\sum_{j=1}^{k}(H^TLH)_{jj}=Tr(H^TLH)$ 。

此外注意到 $H^TH =I,H_{n \times k}=\mathbf{[h_1,h_2,...,h_k}]$ 。

综上所述，问题就变成了一个优化问题： $\min_{H} Tr(H^TLH) \ s.t.H^TH=I$ 。

利用拉格朗日乘子法求得： $LH=\lambda H$ ,即H就是L中k个最小特征值所对应的特征向量（按列向量形式组成的矩阵）。

使用RatioCut时，先计算L的k个特征向量，按行进行归一化。

b.Ncut：

NCut所考虑的最小划分函数是： $Ncut(A_1,A_2,...,A_k)=\frac{1}{2}\sum_{i\in A_i}^{k}\frac{W(A_i,\bar{A_i})}{vol(A_i)}=\sum_{i=1}^{k}\frac{cut(A_i,\bar{A_i})}{vol(A_i)}$ ，

指示向量定义为： $\mathbf{h_{j}}\in [\mathbf{h_1,h_2,...,h_k}]\in R^n \ and\ \mathbf{h_{i,j}}=\left\{\begin{matrix} \frac{1}{\sqrt{vol(A_j)}},v_i\in A_j\\0,v_j \notin A_j\end{matrix}\right.$

则问题可以转换为： $\min_{H} Tr(H^TLH) \ s.t.H^TDH=I$ 。 $H^TDH=H^TD^{\frac{1}{2}}D^{\frac{1}{2}}H=H^TD^{\frac{T}{2}}D^{\frac{1}{2}}H=(D^{\frac{1}{2}}H)^TD^{\frac{1}{2}}H=F^TF$ ,所以令 $F=D^{\frac{1}{2}}H$ ,将 $H=D^{-\frac{1}{2}}F$ 带入目标函数，得到 $\min_{F} Tr(F^TD^{-\frac{1}{2}}LD^{-\frac{1}{2}}H) \ s.t.F^TF=I$ 。其中 $D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$ 称为归一化的拉普拉斯矩阵（记作 $L_{sym}$ )。当使用Ncut时，先计算归一化拉普拉斯矩阵的特征向量F，然后按行标准化F，（注意，此时并不需要算出H），标准化后，再进行一次kmeans聚类即可。

（4）算法流程与代码：

本文参考：

(1)A Tutorial on Spectral Clustering Ulrike von Luxburg

(2) https://www.cnblogs.com/pinard/p/6221564.html

猜你喜欢