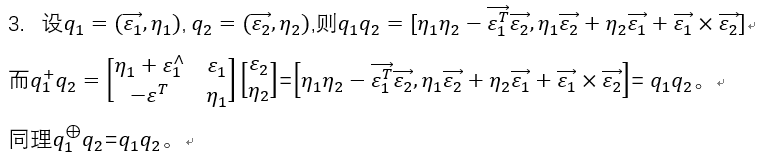SLAM十四讲第二次作业-深蓝学院

1. r(A)=n:矩阵A的秩等于未知数的个数。
2. ⾼斯消元法：通过用初等行变换将增广矩阵化为行阶梯阵，然后通过回代求解线性方程组的解。原理是将方程组中每个方程含有的未知数的个数降到最低，并且最下面的方程含有的未知数的个数最少。
3. QR分解：把矩阵分解成一个列向量正交矩阵与一个上三角矩阵的积。原理是将矩阵每个列作为一个基本单元，将其化为正交的基向量与在这个基向量上的投影长度的积。
4. Cholesky 分解：将一个对称正定矩阵分解成一个下三角矩阵与其共轭转置之乘积。
5. 代码见：eigenMatrix.cpp与CMakeLists.txt
   eigenMatrix.cpp文件

/*求解 A * x = B 这个方程*/

#include <iostream>
#include <Eigen/Core>
#include <Eigen/Dense>
#include <Eigen/Cholesky>

using namespace std;
using namespace Eigen;

#define MATRIX_SIZE 100

int main( int argc,char** argv )
{
    MatrixXd A_pre = MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
    MatrixXd A = A_pre.transpose()*A_pre ;                  //使得A为正定对称矩阵，才能使得cholesky分解成功
    VectorXd B = VectorXd::Random( MATRIX_SIZE );
    VectorXd x = A.colPivHouseholderQr().solve(B);          //调用QR分解求解
    VectorXd y = A.llt().solve(B);                          //调用cholesky分解求解

    cout <<"A*x=B方程的解为\n"<< x << endl;
    cout <<"A*y=B方程的解为\n"<< y << endl;
}

CMaleLists.txt文件

cmake_minimum_required( VERSION 2.8 )
project( useEigen )

set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-O3" )

# 添加Eigen头文件
include_directories( "/usr/include/eigen3" )

add_executable( eigen eigenMatrix.cpp )

代码见：useGeometry.cpp与CMakeLists.txt

useGeometry.cpp文件

#include <iostream>
#include <cmath>
#include <Eigen/Core>
#include <Eigen/Geometry>

using namespace std;
using namespace Eigen;

int main(int arcg,char** argv)
{
    Quaterniond q1 = Quaterniond(0.55,0.3,0.2,0.2).normalized();   //定义并归一化四元数
    Quaterniond q2 = Quaterniond(-0.1,0.3,-0.7,0.2).normalized();
    Vector3d t1 ,t2,p1,p,p2;
    t1 << 0.7,1.1,0.2;
    t2 << -0.1,0.4,0.8;
    p1 << 0.5,-0.1,0.2;
  

    Isometry3d T_cw1 = Isometry3d::Identity();
    T_cw1.rotate ( q1 );
    T_cw1.pretranslate ( t1 );

    Isometry3d T_cw2 = Isometry3d::Identity();
    T_cw2.rotate ( q2 );
    T_cw2.pretranslate ( t2 );



    p = T_cw1.inverse() *p1;   //不能用转置，因为这里不是纯旋转，见书42页
    p2 = T_cw2 *p ;

    cout<<"p2 = "<<p2.transpose()<<endl;
}

CMakeLists.txt文件

cmake_minimum_required( VERSION 2.8 )
project( geometry )

# 添加Eigen头文件
include_directories( "/usr/include/eigen3" )

add_executable( eigenGeometry eigenGeometry.cpp )

1. 证明：
   设某个单位正交基 $(e_1,e_2,e_3)$经过一次旋转变成了 $(f_1,f_2,f_3)$，那么旋转矩阵
   $R = \begin{bmatrix} e_1^T \\ e_2^T \\ e_3^T \end{bmatrix} \cdot \begin{bmatrix} f_1 & f_2 &f_3 \end{bmatrix} \\ \because \begin{bmatrix} e_1^T \\ e_2^T \\ e_3^T \end{bmatrix} \cdot \begin{bmatrix} e_1& e_2 &e_3 \end{bmatrix} = I \\ \begin{aligned}\therefore R^T \cdot R &= \begin{bmatrix} f_1^T \\ f_2^T \\ f_3^T \end{bmatrix} \cdot \begin{bmatrix} e_1 & e_2 & e_3 \end{bmatrix} \cdot \begin{bmatrix} e_1^T \\ e_2^T \\ e_3^T \end{bmatrix} \cdot \begin{bmatrix} f_1 & f_2 &f_3 \end{bmatrix} \\ &= \begin{bmatrix} f_1^T \\ f_2^T \\ f_3^T \end{bmatrix} \cdot I \cdot \begin{bmatrix} f_1 & f_2 &f_3 \end{bmatrix} \\ &= I \end{aligned} \\ \therefore R^T \cdot R=I$
   $\begin{aligned} |R| &= \begin{vmatrix} e_1^T \\ e_2^T \\ e_3^T \end{vmatrix} \cdot \begin{vmatrix} f_1 & f_2 &f_3 \end{vmatrix} \\ &=1 \\ \therefore detR = \pm 1 \end{aligned}$
   又因为单位正交基的模为+1，
   $\therefore detR = +1$
   所以 $R^TR=I$，且 $detR=+1$
2. 证明：
   四元数由四个数组成，有一个实部和三个虚部，形如： $q=q_0+q_1i+q_2j+q_3k$。那么上述的 $\varepsilon = [ q_1,q_2,q_3]^T \in \mathbb{R}^3$， $\eta = q_0 \in \mathbb{R}$。
   所以 $\varepsilon$和 $\eta$的维度分别为 3和1。
3. 证明： （一定要注意四元数实部与虚部的顺序,这里实部在最后）
   令 $q_1=[x_1,y_1,z_1,w_1],q_2=[x_2,y_2,z_2,w_2]$，其中 $w_1,w_2$为实部
   $\begin{aligned} q_1\cdot q_2 &=(w_1x_2+x_1w_2+y_1z_2-z_1y_2)i \\&+(w_1y_2-x_1z_2+y_1w_2+z_1x_2) j \\&+(w_1z_2+x_1y_2-y_1x_2+z_1w_2) k \\&+w_1w_2-x_1x_2-y_1y_2-z_1z_2 \end{aligned}$
   $\begin{aligned} q_1^+q_2 &= \begin{bmatrix} w_1 & -z_1 & y_1 & x_1 \\z_1 & w_1 & -x_1 & y_1\\-y_1 & x_1 & w_1 & z_1 \\ -x_1 & -y_1 & -z_1 & w_1 \end{bmatrix} \begin{bmatrix} x_2 \\ y_2 \\z_2 \\w_2 \end{bmatrix} \\ &= \begin{bmatrix} w_1x_2+x_1w_2+y_1z_2-z_1y_2 \\ w_1y_2-x_1z_2+y_1w_2+z_1x_2 \\ w_1z_2+x_1y_2-y_1x_2+z_1w_2 \\ w_1w_2-x_1x_2-y_1y_2-z_1z_2 \end{bmatrix} \\&=(w_1x_2+x_1w_2+y_1z_2-z_1y_2)i \\&+(w_1y_2-x_1z_2+y_1w_2+z_1x_2) j \\&+(w_1z_2+x_1y_2-y_1x_2+z_1w_2) k \\&+w_1w_2-x_1x_2-y_1y_2-z_1z_2 \\ &= q_1\cdot q_2 \end{aligned}$
   所以： $q_1 \cdot q_2 = q_1^+q_2$
   同理可证： $q_1 \cdot q_2 = q_2^ \oplus q_1$

证明方法二：


证明：

如上图， $V_{rot}$是由 $V$通过旋转得到，旋转轴是K，旋转的角度为 $\theta$，用旋转矩阵R表示该旋转，即为： $V_{rot} = R \cdot V$, 且 $K$为单位向量， $||\vec{K} || =1$,
$V=V_\perp + V_\parallel$,
$V_\perp = V-V_\parallel = -K \times (K \times V)$，
$V_\parallel = (K \cdot V) \cdot K = K K^T V$,
则垂直分量和平行分量各自的旋转分量为：
$V_{\parallel rot} = V_\parallel$
$V_{\perp rot} = cos\theta V_\perp+sin\theta K \times V$
$\begin{aligned}\therefore V_{rot} &= V_{\parallel rot} + V_{\perp rot} \\&= V_\parallel + cos\theta V_\perp +sin\theta K\times V \\&=V_\parallel + cos\theta(V-V_\parallel) + sin\theta K \times V \\&= cos\theta V + (1-cos\theta)V_\parallel +sin\theta K \times V \\&= cos\theta V+ (1-cos\theta) K K^T V + sin\theta K^\times V \\&=R \cdot V \end{aligned}$
$\therefore R = cos\theta I + (1-cos\theta) K K^T + sin\theta K^\times$
$\therefore R = cos\theta I + (1-cos\theta)nn^T +sin\theta n^\times$

证明：
（1） $p^{'}$的实部为0
假定点p的坐标为 $p(x,y,z)$，则用四元数表示为： $p=[0,x,y,z]=xi+yj+zk$,
令 $q=[cos\frac{\theta}{2} ,nsin\frac{\theta}{2}]=cos\frac{\theta}{2}+n_x sin\frac{\theta}{2}i+n_y sin\frac{\theta}{2}j+n_z sin\frac{\theta}{2}k$
$\because q^\ast=[cos\frac{\theta}{2} ,-\mathbf{n}sin\frac{\theta}{2}],q^{-1}=q^\ast/||q||^2$
则 $q^{-1} = [cos\frac{\theta}{2} ,-nsin\frac{\theta}{2}]/||q||^2=(cos\frac{\theta}{2} - n_x sin\frac{\theta}{2}i - n_y sin\frac{\theta}{2}j - n_z sin\frac{\theta}{2}k)/||q||^2$
$\begin{aligned} \therefore p^{'} &= qpq^{-1} \\&=[cos\frac{\theta}{2} ,nsin\frac{\theta}{2}] [0,x,y,z] [cos\frac{\theta}{2} ,-nsin\frac{\theta}{2}]/||q||^2\\&=(cos\frac{\theta}{2}+n_x sin\frac{\theta}{2}i+n_y sin\frac{\theta}{2}j+n_z sin\frac{\theta}{2}k)(xi+yj+zk)((cos\frac{\theta}{2} - n_x sin\frac{\theta}{2}i - n_y sin\frac{\theta}{2}j - n_z sin\frac{\theta}{2}k)/||q||^2) \end{aligned}$
将所有的实数取出,且忽略 $||q||^2$，则：
$x n_x cos\frac{\theta}{2} sin\frac{\theta}{2} + y n_y cos\frac{\theta}{2} sin\frac{\theta}{2} +z n_z cos\frac{\theta}{2} sin\frac{\theta}{2} \\ + (-1) x n_x sin\frac{\theta}{2} x cos\frac{\theta}{2} + y n_x n_z sin\frac{\theta}{2} sin\frac{\theta}{2} + (-1)z n_x n_ysin\frac{\theta}{2} sin\frac{\theta}{2} \\+(-1)y n_y sin\frac{\theta}{2} cos\frac{\theta}{2} + (-1) x n_y n_z sin\frac{\theta}{2} sin\frac{\theta}{2} + z n_x n_y sin\frac{\theta}{2} sin\frac{\theta}{2} \\+ x n_y n_z sin\frac{\theta}{2} sin\frac{\theta}{2} +(-1) y n_x n_z sin\frac{\theta}{2}sin\frac{\theta}{2} + (-1) z n_z sin\frac{\theta}{2}cos\frac{\theta}{2} \\ \\=0$
所以实部为0，即 $p^{'}$的实部为0。

（2） $p^{'} = Qp$，写出矩阵 $Q$
$\begin{aligned} p^{'} &= qpq^{-1} \\ &= q^+ p^+q^{-1} \\&= q^+ q^{-1^\oplus}p \end{aligned}$
$\therefore Q= q^+ q^{-1^\oplus}$
假定四元数 $q=[x,y,z,w]$，其中 $w$是实部，那么 $q^{-1}=[-x,-y,-z,w]/||q||^2$
$q^+ = \begin{bmatrix} \eta1 + \varepsilon ^\times & \varepsilon \\ -\varepsilon^T & \eta \end{bmatrix}=\begin{bmatrix} w & -z & y & x\\z & w & -x & y\\-y & x & w & z \\ -x & -y & -z & w\end{bmatrix}$,
$q^{-1^\oplus}= \begin{bmatrix} \eta1 - (-\varepsilon) ^\times & -\varepsilon \\ -(-\varepsilon)^T & \eta \end{bmatrix}/||q||^2 = \frac{1}{||q||^2 }\cdot \begin{bmatrix} \eta1 + \varepsilon ^\times & -\varepsilon \\ \varepsilon^T & \eta \end{bmatrix}=\frac{1}{||q||^2 }\cdot \begin{bmatrix} w & -z & y & -x\\z & w & -x & -y\\-y & x & w & -z \\ x & y & z & w\end{bmatrix}$
$\begin{aligned} \therefore Q &= q^+ q^{-1^\oplus} \\&= \frac{1}{||q||^2 }\cdot\begin{bmatrix} w & -z & y & x\\z & w & -x & y\\-y & x & w & z \\ -x & -y & -z & w\end{bmatrix}\begin{bmatrix} w & -z & y & -x\\z & w & -x & -y\\-y & x & w & -z \\ x & y & z & w\end{bmatrix} \\&= \frac{1}{||q||^2 }\cdot \begin{bmatrix}w^2+x^2-y^2+z^2& 2xy-2zw & 2wy+2xz & 0\\ 2xy+2zw& w^2-x^2+y^2-z^2 & 2yz-2xw & 0\\2xz-2yw & 2yz+2xw & w^2-x^2-y^2+z^2 & 0 \\ 0 & 0 & 0 & w^2+x^2+y^2+z^2\end{bmatrix} \end{aligned}$

证明方法二：

1. for(atuo& a: avec)
   范围for循环，用a遍历avec中的每个量；
2. for(atuo& a: avec)
   自动类型推导，根据a获得的值，用auto自动推断出a的类型；
3. [](const A&a1,const A&a2){return a1.index<a2.index;})
   运用了lambda表达式。
4. begin()