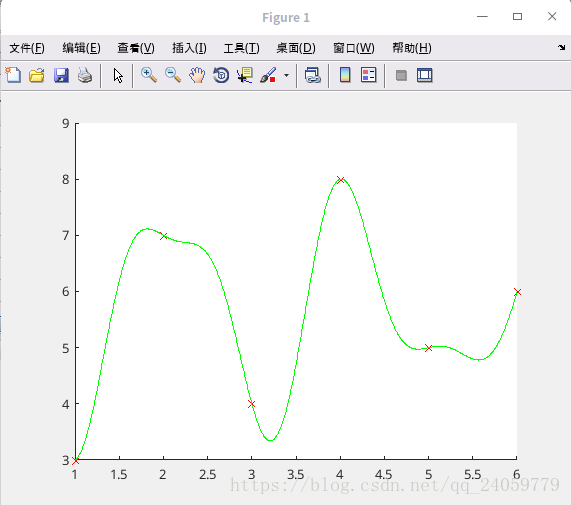
code:1.分析数据需要用什么函数来拟合,给定已知sin函数的时候好拟合,但是未知函数是几次,未知具体函数什么样子的时候拟合的时候需要自己观察数据,并选择相应的模型拟合,我自己编写了一段code,拟合一下试试算法的实用性.
x=[1,3,5,6,2,4]';
y=[3,4,5,6,7,8]';
plot(x,y,'rx');
plot(x,y,'rx');
%沿着x增大的方向模拟几个点的线,看情况有点像书上的sin函数cos函数的交替,试一试
X=linspace(1,6,1000)';
p(:,1)=ones(6,1);P(:,1)=ones(1000,1);
for j=1:15
p(:,2*j)=sin(j/2*x);p(:,2*j+1)=cos(j/2*x);
P(:,2*j)=sin(j/2*X);P(:,2*j+1)=cos(j/2*X);
end
t=p\y;
F=P*t;
figure(1);clf;hold on;
plot(x,y,'rx');
plot(X,F,'g-');
矩阵的奇异值分解具体请见blog: https://www.cnblogs.com/lzllovesyl/p/5243370.html
正交投影见blog:https://blog.csdn.net/tengweitw/article/details/41174555
正交投影约束条件中的P矩阵需要用到pca:第13章,第17章一起看了,看看这个
http://blog.codinglabs.org/articles/pca-tutorial.html
简单总结一下PCA:在某种合理的情况下数据降维可以大大减少运算时间和内存空间,但是这种降维度方式必须是合理的,例如上文中的两个事例-淘宝店和男性女性就是为了说明数据降维不是随便的,在数据相关性,数据依赖性比较强的数据之间可以降维.
同理主成分分析法在降维时也必须有合理性--
A与B的内积,等于A在B方向上的投影乘B标量向量长度,
要描述一个向量,首先要确定一组基向量,然后给出在各个直线上的投影值.
从内积的定义可以看到,如果基底(B)的模是1,那么就可以方便的用向量点乘基而直接获得在其新基上的坐标.
基底变换可以用矩阵表示,假设由m个n维向量组成(n*m)矩阵X,现在用n维空间中的r个正交向量积来左乘,如下图,就达到了降纬的效果,可以看到原本a1表示的是n维度的坐标值,现在被换算成左边一竖列R维度的坐标值,由原来的n维度降低到了r维度,一切都归功于在原坐标系原维度的m个n维矩阵左边乘了该空间中不满秩的正交向量基.

现在要解决R的维数怎么取,降维到什么空间能够保证数据保存最完整的前提下缩减时间空间复杂度.上文中举了一个二维降到一维的例子.
一条直线上点的方差可以表示为:每一个点对均值做差再平方,然后把这些值加起来.当这个和值越大,说明分开的效果越好,数据独立性越好,不存在重复的数据.
将一组n维数据降为k维,目标是选择k个单位正交基,使得原始数据变换到这组基上后,各字段两两协方差为0,而字段间的尽可能大,
x*x' !
将协方差矩阵对角化:即除对角线外的其它元素化为0,并且在对角线上将元素按大小从上到下排列,这样我们就达到了优化目的
寻找一个矩阵P,满足PCPTPCPT是一个对角矩阵,并且对角元素按从大到小依次排列,那么P的前K行就是要寻找的基,用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。
P是协方差矩阵的特征向量单位化后按行排列出的矩阵,其中每一行都是C的一个特征向量。如果设P按照ΛΛ中特征值的从大到小,将特征向量从上到下排列,则用P的前K行组成的矩阵乘以原始数据矩阵X,就得到了我们需要的降维后的数据矩阵Y。
https://zhuanlan.zhihu.com/p/30145700
这篇博客讲解了PCA中k值的取值什么时候是合理的,在k取不同值的时候对真实数据保存比例.
对书中正交映射限制参数问题代码的理解:
其实
x=linspace(-3,3,50)';
X=linspace(-3,3,1000)';
for i=1:7
p(:,i)=x.^(i-1);
P(:,i)=X.^(i-1);
end
t1=p\y;
t2=(p*diag([1,1,1,0,0,0,0]))\y;
f1=P*t1;
f2=P*t2;
figure(1);clf;hold on; plot(x,y,'rx');plot(X,f1,'g-');
figure(2);clf;hold on; plot(x,y,'rx');plot(X,f2,'g-');
这部分对P的取值和后面的PCA技术相关性不是太大,举个简单的例子,在我已知一个由二次函数构造的函数样本,前几次我用6次的多项式函数去模拟函数,可以的到如图所示的所示

当我用P正交法,用其乘一个对角化矩阵,把其降维,不但可以节省运算的时间复杂度,更能够使得过拟合问题得到解决,好处太多

这两个图别看这一样,放大之后一顿切换明显能看到第一个6次复杂度的过拟合.2次的方程没毛病.
这第一个正交化的代码的含义就是简单的把过拟合过估计的部门参数抹掉,解决过拟合,参数复杂度过多的问题.
L2约束的最小二乘学习法:
P的使用实在是太扯淡了,自己随便改,根本不是按照pca来的,只是稍微使用了pca里面的矩阵降维的思想.所以实际中使用L2的约束条件比较好,
学习拉格朗日对偶原理重要的是理解构造所得的原始问题和原函数的等价性,以及原始问题和对偶问题解得等价性
https://www.cnblogs.com/90zeng/p/Lagrange_duality.html
kernal fuction是比较好,方法比较通用,但是你得很好的拟合啊,那参数hh能够随便设置么,得需要一遍一遍试才可以吧.所以针对简单的二次函数,拟合效果不用想,肯定很差,但是还要试试吧.

样本点只取5个点,拟合成了什么样子了都

所以所有人都在强调,大数据的重要性,当样本数为50的时候,拟合的明显就好的很多很多,但是很容易发现,这种拟合属于过度拟合,在五十个样本比较集中地地方拟合的非常好,但是在边缘部分,因为样本分布越来越稀疏,可以发现对未知样本点的预测能力极差,图像和点完全不拟合,所以需要使用接下来介绍的防止过拟合的约束条件进行阻止过拟合,让样本在未知的领域具有较强的预测能力
x=[-2,-1,0,1,2]';
>> y=x.^2;
>> p(:,2)=x;
>> p(:,1)=1;
>> p(:,3)=x.^2;
>> t0=rand(3,1);
>> e=0.1;
for o=1:1000
i=ceil(rand*5);
k=p(i,:);
t=t0-e*k'*(k*t0-y(i));
if (t-t0)<0.001,break,end
t0=t;
end
X=linspace(-3,3,1000)';
>> P(:,2)=X;
>> P(:,1)=1;
>> P(:,3)=X.^2;
>> F=P*t;
>> figure(1);clf;hold on;
>> plot(x,y,'rx');
>> plot(X,F,'g-');
代码段2:
x=linspace(-3,3,50)';
y=x.^2;
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
for o=1:1000
i=ceil(rand*50);
ki=exp(-(x-x(i)).^2/hh);
t=t0-e*ki*(ki'*t0-y(i));
if norm(t-t0)<0.001,break,end
t0=t;
end
K=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
>> F=K*t;
>> figure(1);clf;hold on;
>> plot(x,y,'rx');
>> plot(X,F,'g-');L2约束条件的最小二乘法
源代码:
x=[1,3,5,6,2,4]';
y=[3,4,5,6,7,8]';
plot(x,y,'rx');
plot(x,y,'rx');
%沿着x增大的方向模拟几个点的线,看情况有点像书上的sin函数cos函数的交替,试一试
X=linspace(1,6,1000)';
p(:,1)=ones(6,1);P(:,1)=ones(1000,1);
for j=1:15
p(:,2*j)=sin(j/2*x);p(:,2*j+1)=cos(j/2*x);
P(:,2*j)=sin(j/2*X);P(:,2*j+1)=cos(j/2*X);
end
t=p\y;
F=P*t;
figure(1);clf;hold on;
plot(x,y,'rx');
plot(X,F,'g-');
t2=(p'*p+0.1*eye(31))\p'*y;
>> F2=P*t2;
>> figure(2);clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

虽然不太好讲,但是也要强行解释一波,确实对过去的过拟合问题得到了很大程度的改善,但是这个图像的变化太剧烈了,我再去试试二次函数的那个看看效果是什么样子,希望不会图像不会有太大的变化,beg
x=linspace(-3,3,50)';
y=x.^2;
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
t2=(k1^2+0.1*eye(50))\k1*y;
F2=K1*t2;
figure(1);clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
figure(2);clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

这个还不是比较明显的,因为我模拟的二次函数是没有噪声的二次函数,只能看出来确实图二拟合的效果没有图一好,下面选取有噪声的二次函数模拟一下
源代码:
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
t2=(k1^2+0.1*eye(50))\k1*y;
F2=K1*t2;
figure(1);clf;hold on;axis([-3 3 -10 10]);plot(x,y,'rx');plot(X,F1,'g-');
figure(2);clf;hold on;axis([-3 3 -10 10]);plot(x,y,'rx');plot(X,F2,'g-');

可以看出来:当拟合具有噪声的二次函数的时候图一已经有过拟合的效果了,这样对以后的预测会产生很大的误差,图二使用L2约束的最小二乘法不但使图像更趋于平滑而且减弱了过拟合问题.
模型选择:
涉及到高斯kenal函数的模型参数选择书上给出了相应的方法:交叉验证法:
1把训练样本随机分成m个集合(2-10之间),大小一致
2.对i=1....m循环执行如下操作
(a).对除了第i组的其余样本进行学习得到学习结果fi
(b).把上述没有参加训练的样本作为测试集,对上面的fi进行泛化误差评估,评估函数书上有
3.对各个i的泛化误差的评估值进行平均,得到最终的泛化误差评估值,选择最小的泛化误差评估值对应的参数为最合适的参数
对上面我的二次函数试一试到底什么样的高斯参数才是能够最好拟合的呢?
求矩阵A的最大值的函数有3种调用格式,分别是:
(1) max(A):返回一个行向量,向量的第i个元素是矩阵A的第i列上的最大值。
(2) [Y,U]=max(A):返回行向量Y和U,Y向量记录A的每列的最大值,U向量记录每列最大值的行号。
(3) max(A,[],dim):dim取1或2。dim取1时,该函数和max(A)完全相同;dim取2时,该函数返回一个列向量,其第i个元素是A矩阵的第i行上的最大值。
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hhs=2*[0.03 0.3 3].^2;
ls=[0.0001 0.001 0.1];
s=repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x';
u=floor([0:49]/10)+1;
u=u(randperm(50));
for hk=1:length(hhs)
hh=hhs(hk);k=exp(-s/hh);
for i=1:5
ki=k(u~=i,:);kc=k(u==i,:);yi=y(u~=i);yc=y(u==i);
for lk=1:length(ls)
l=ls(lk);
t=(ki'*ki+l*eye(50))\(ki'*yi);fc=kc*t;
g(hk,lk,i)=mean((fc-yc).^2);
end,end,end
[gl,ggl]=min(mean(g,3),[],2);
[ga,gb]=min(gl);
l=ls(ggl(gb));
hh=hhs(gb);
k=exp(-s/hh);
K=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t=(k^2+l*eye(50))\(k*y);
F=K*t;
figure(1);clf;hold on;plot(x,y,'rx');plot(X,F,'g-');
明显看到在这份参数下二次函数拟合的效果达到更好,更加平滑
l1约束源代码:
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
for o=1:1000
t2=(k1^2+e*pinv(diag(abs(t0))))\k1*y;
if (t2-t0)<0.001,break,end
t0=t2;
end
F2=K1*t2;
figure(1),clf;hold on;plot(x,y,'rx');axis([-3 3 0 10]);plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

效果不比之前差,最关键的是这个l1约束条件下面得到的参数是稀疏,很多0,计算的时间复杂度明显缩小:

可以看到一共50个参数,有一半的参数都是0.
l无穷范数表示的是参数里面的最大值
l0范数表示的是参数里面的非0元素的个数
l1+l2范数约束的最小二乘法:

源代码:
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
for o=1:1000
t2=(k1^2+e*pinv(diag(abs(t0))))\k1*y;
if (t2-t0)<0.001,break,end
t0=t2;
end
t3=(k1^2+e*eye(50))\k1*y;
t4=t2/2+t3/2;
F2=K1*t2;
F3=K1*t3;
F4=K1*t4;
figure(1),clf;hold on;plot(x,y,'rx');axis([-3 3 0 10]);plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');
figure(3),clf;hold on;plot(x,y,'rx');plot(X,F3,'g-');
figure(4),clf;hold on;plot(x,y,'rx');plot(X,F4,'g-');




具体效果需要全屏切换观察,具体效果的好坏仁者见仁智者见智,我以后会使用l1和l2结合的最小二乘法来进行计算.
鲁棒学习:
https://mp.csdn.net/postedit/82763849
使用l2损失最小化学习异常值会使得残差平方和剧增所以要使用残差和线性增长的l1损失最小函数来验证训练样本的合理性,对不合理的样本予以剔除掉.但是l1绝对值鲁棒学习法有一个很明显的缺点就是不能求导,要借助于变化成为二次函数之后才能求导,而且高的鲁棒性与学习模型并不十分吻合,为0的时候会得到最好的鲁棒性,实际学习效果旺旺并不能达到预期,所以为了能够很好的取得有效性和鲁棒性的平衡发明huber算法,l2的部分是使得模型更贴近样本,l1的部分是为了使得它有更好的鲁棒性.
有效果有效果 源代码:
x=linspace(-4,4,10)';
X=linspace(-4,4,1000)';
y=x+0.2*randn(10,1);
y(1)=-8;y(8)=9;y(4)=-9;y(3)=18;
p(:,1)=ones(10,1);
p(:,2)=x;
P(:,1)=ones(1000,1);P(:,2)=X;
t1=p\y;
F1=P*t1;
e=1;
for o=1:1000
r=abs(p*t1-y);
w=ones(10,1);
w(r>e)=e./r(r>e);
t2=(p'*(repmat(w,1,2).*p))\(p'*(w.*y));
if norm(t2-t1)<0.001,break,end
t1=t2;
end
F2=P*t2;
figure(1),clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

图基:
x=linspace(-4,4,10)';
X=linspace(-4,4,1000)';
y=x+0.2*randn(10,1);
y(8)=9;y(4)=-9;
p(:,1)=ones(10,1);
p(:,2)=x;
P(:,1)=ones(1000,1);P(:,2)=X;
t1=p\y;
e=1;
for o=1:1000
r=abs(p*t1-y);
w=zeros(10,1);
w(r<=e)=(1-r(r<=e).^2/e^2).^2;
t2=(p'*(repmat(w,1,2).*p))\(p'*(w.*y));
if norm(t2-t1)<0.001,break,end
t1=t2;
end
F1=P*t2;
>> t3=p\y;
>> for o=1:1000
r=abs(p*t3-y);
w=ones(10,1);
w(r>e)=e./r(r>e);
t4=(p'*(repmat(w,1,2).*p))\(p'*(w.*y));
if norm(t4-t3)<0.001,break,end
t3=t4;
end
>> F2=P*t4;
>> figure(1),clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
>> figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

图基算法明显效果比huber还要好,但是要注意的一点是,图基算法的初始值一定要是对的,初始值错了,算法基本就崩溃了,什么奇异值精确度的报错;
rand('state',0);randn('state',0);
n=50;N=1000;x=linspace(-3,3,n)';X=linspace(-3,3,N)';
pix=pi*x;y=sin(pix)+0.1*x+0.2*randn(n,1);
y(n/2)=-0.5;
hh=2*0.3^2;l=0.1;e=0.1;
k=exp(-(repmat(x.^2,1,n)+repmat(x.^2',n,1)-2*x*x')/hh);
t1=k\y;
K=exp(-(repmat(X.^2,1,n)+repmat(x.^2',N,1)-2*X*x')/hh);
F1=K*t1;
for o=1:100
end
t0=randn(n,1);
for o=1:100
t=(k^2+l*pinv(diag(abs(t0))))\(k*y);
if norm(t-t0)<0.001,break,end
t0=t;
end
F2=K*t;
t3=k\y;
for o=1:100
r=abs(k*t3-y);w=ones(n,1);w(r>e)=e./r(r>e);
t2=(k'*(repmat(w,1,50).*k))\(k'*(w.*y));
Z=k*(repmat(w,1,n).*k)+l*pinv(diag(abs(t3)));
t4=(Z+0.00001*eye(n))\(k*(w.*y));
if norm(t4-t3)<0.001,break,end
t3=t2;
t3=t4;
end
F3=K*t2;
F4=K*t4;
figure(1),clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');
figure(3),clf;hold on;plot(x,y,'rx');plot(X,F3,'g-');
figure(4),clf;hold on;plot(x,y,'rx');plot(X,F4,'g-');



分析:
图一没有处理过的线过拟合受异常值干扰严重
图二的l1约束后明显解决了过拟合的问题,但是仍然受异常值影响严重
图三单单使用huber来拟合可以解决鲁棒性的问题即受异常值的影响较小,但是不能解决过拟合的问题
图四使用huber+l1约束,,能够很好的解决过拟合和鲁棒性的问题