编程菜鸟到大佬之路：数据结构（二）

数据结构C++版——邓俊辉课堂笔记

第一章 绪论

---

复杂度度量

• 时间复杂度

  • 问题实例的规模往往是决定计算成本的主要因素。一般地，问题规模越接近，相应的计算成本也越接近；而随着问题规模的扩大，计算成本通常也呈上升趋势。
  • 执行时间的这一变化趋势可表示为输入规模的一个函数，称作该算法的时间复杂度（time complexity）。具体地，特定算法处理规模为n的问题所需的时间可记作T(n)。
  • 根据规模并不能唯一确定具体的输入，规模相同的输入通常都有多个，而算法对其进行处理所需时间也不尽相同。
  • 严格说来，以上定义的T(n)并不明确。为此需要再做一次简化，即从保守估计的角度出发，在规模为n的所有输入中选择执行时间最长者作为T(n)，并以T(n)度量该算法的时间复杂度。

• 渐进复杂度

  • 对于同一问题的两个算法A和B，通过比较其时间复杂度 $T_A(n)$和 $T_B(n)$，即可评价二者对于同一输入规模n的计算效率高低。然而，藉此还不足以就其性能优劣做出总体性的评判，比如对于某些问题， 一些算法更适用于小规模输入，而另一些则相反。
  • 在评价算法运行效率时，我们往往可以忽略其处理小规模问题时的能力差异，转而关注其在处理更大规模问题时的表现。这种着眼长远、更为注重时间复杂度的总体变化趋势和增长速度的策略与方法，即所谓的渐进分析（ asymptotic analysis）。

• 大O记号

  • 首先关注T(n)的渐进上界。为此可引入所谓“大O记号”（big-O notation）。具体地，若存在正的常数c和函数f(n)，使得对任何n >> 2都有 $T(n)\leq c∙f(n)$则可认为在n足够大之后， f(n)给出了T(n)增长速度的一个渐进上界。此时，记之为：T(n) = O(f(n))。
    • 对于任一常数c > 0，有O(f(n)) = O(c∙f(n))；
    • 对于任意常数a > b > 0，有O( $n^a+n^b$) = O( $n^a$) 。
    • 在大O记号的意义下，函数各项正的常系数可以忽略并等同于1。
    • 多项式中的低次项均可忽略，只需保留最高次项。

• 环境差异

  • 在实际环境中直接测得的执行时间T(n)，虽不失为衡量算法性能的一种指标，但作为评判不同算法性能优劣的标准，其可信度值得推敲。
  • 事实上，即便是同一算法、同一输入，在不同的硬件平台上、不同的操作系统中甚至不同的时间，所需要的计算时间都不尽相同。

• 基本操作

  • 一种自然且可行的解决办法是，将时间复杂度理解为算法中各条指令的执行时间之和。
  • 不妨将T(n)定义为算法所执行基本操作的总次数。也就是说，T(n)决定于组成算法的所有语句各自的执行次数，以及其中所含基本操作的数目。

• 起泡排序

  • bubblesort1A()算法由内、外两层循环组成。
  • 内循环从前向后，依次比较各对相邻元素，如有必要则将其交换。故在每一轮内循环中，需要扫描和比较n-1对元素，至多需要交换n-1对元素。
  • 元素的比较和交换，都属于基本操作，故每一轮内循环至多需要执行2(n-1)次基本操作。
  • 外循环至多执行n-1轮。因此，总共需要执行的基本操作不会超过 $2(n-1)^2$次。
  • 若以此来度量该算法的时间复杂度，则有 $T(n)=O(2(n-1)^2)$，根据大O记号的性质，可进一步简化和整理为： $T(n)=O(2n^2-4n+2)=O(2n^2)=O(n^2)$。

• 最坏、最好与平均情况

  • 以大O记号形式表示的时间复杂度，实质上是对算法执行时间的一种保守估计，对于规模为n的任意输入，算法的运行时间都不会超过O(f(n))。
  • 比如：起泡排序算法复杂度 $T(n) = O(n^2)$意味着，该算法处理任何序列所需的时间绝不会超过 $O(n^2)$。
  • 的确需要这么长计算时间的输入实例，称作最坏实例或最坏情况（worst case）。
  • 需强调的是，这种保守估计并不排斥更好情况甚至最好情况（best case）的存在和出现。比如，对于某些输入序列，起泡排序算法的内循环的执行轮数可能少于n-1，甚至只需执行一轮。
  • 当然，有时也需要考查所谓的平均情况（average case），也就是按照某种约定的概率分布，将规模为n的所有输入对应的计算时间加权平均。

• 大 $\Omega$记号

  • 为了对算法的复杂度最好情况做出估计，需要借助另一个记号。
  • 如果存在正的常数c和函数g(n)，使得对于任何n >> 2都有 $T(n)\geq c∙g(n)$，就可以认为，在n足够大之后，g(n)给出了T(n)的一个渐进下界。此时，我们记之为：T(n) = $\Omega$(g(n))这里的 $\Omega$称作“大 $\Omega$记号” （big-omega notation）。
  • 与大O记号恰好相反，大 $\Omega$记号是对算法执行效率的乐观估计，对于规模为n的任意输入，算法的运行时间都不低于 $\Omega$(g(n))。

• 大 $\Theta$记号

  • 借助大O记号、大 $\Omega$记号，可以对算法的时间复杂度作出定量的界定，亦即，从渐进的趋势看，T(n)介于 $\Omega$(g(n))与O(f(n))之间。
  • 若恰巧出现g(n) = f(n)的情况，则可以使用另一记号来表示。
  • 如果存在正的常数c1 < c2和函数h(n)，使得对于任何n >> 2都有 $c1∙h(n) \leq T(n) \leq c2∙h(n)$，就可以认为在n足够大之后， h(n)给出了T(n)的一个确界。此时，我们记之为：T(n) = $\Theta$(h(n))。
  • 这里的 $\Theta$称作“大 $\Theta$记号” （big-theta notation），它是对算法复杂度的准确估计，对于规模为n的任何输入，算法的运行时间T(n)都与 $\Theta$(h(n))同阶。

• 大O记号，大 $\Omega$记号，大 $\Theta$记号：
  

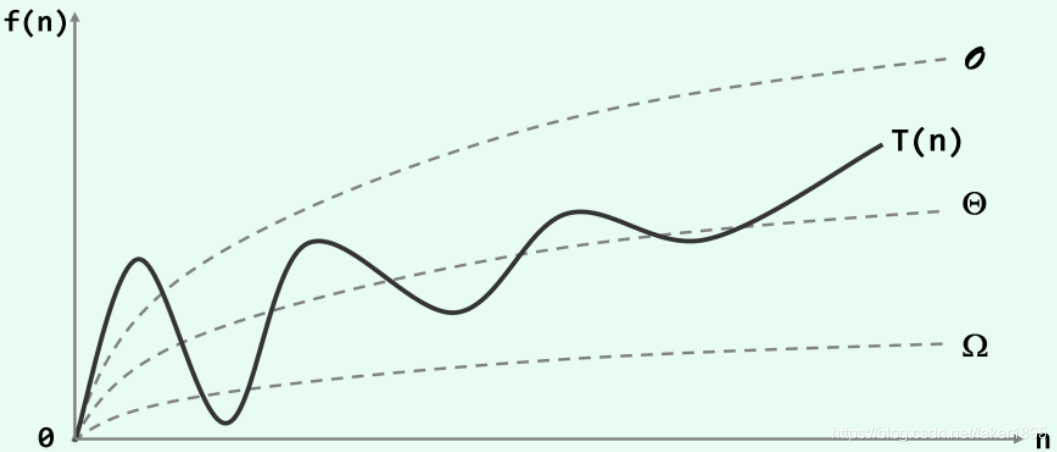
• 空间复杂度

  • 除了执行时间的长短，算法所需存储空间的多少也是衡量其性能的一个重要方面，此即所谓的空间复杂度（space complexity）。
  • 实际上， 以上针对时间复杂度所引入的几种渐进记号，也适用于对空间复杂度的度量， 其原理及方法基本相同。
  • 空间复杂度通常并不计入原始输入本身所占用的空间，对于同一问题，这一指标对任何算法都是相同的。反之， 其它（如转储、中转、索引、映射、缓冲等）各个方面所消耗的空间，则都应计入。
  • 就渐进复杂度的意义而言，在任一算法的任何一次运行过程中所消耗的存储空间，都不会多于其间所执行基本操作的累计次数。
  • 实际上根据定义，每次基本操作所涉及的存储空间，都不会超过常数规模；纵然每次基本操作所占用或访问的存储空间都是新开辟的，整个算法所需的空间总量，也不过与基本操作的次数同阶。从这个意义上说，时间复杂度本身就是空间复杂度的一个天然的上界。

复杂度分析

• 常数O(1)

  • 运行时间可表示和度量为T(n) = O(1)的这一类算法，统称作“常数时间复杂度算法”（constant-time algorithm）。
  • 一般地， 仅含一次或常数次基本操作的算法均属此类。
  • 此类算法通常不含循环、分支、子程序调用等，但也不能仅凭语法结构的表面形式一概而论。
  • 算法仅需常数规模的辅助空间即仅需O(1)辅助空间的算法，亦称作就地算法（ in-place algorithm）。

• 对数O(logn)

  • 问题与算法
    • 考查如下问题：对于任意非负整数，统计其二进制展开中数位1的总数。
    • 整数二进制展开中数位1总数的统计：

      int countOnes(unsigned int n) 
      { 	//统计整数n的二进制展开中数位1的总数：O(logn)
      	int ones = 0; //计数器复位
      	while (n > 0) 
      	{	//在n缩减至0之前循环 
       		ones += (1 & n); //检查最低位，若为1则计数
       		n >>= 1; //右移一位
      	}
      	return ones;    //返回计数
      } 	//等效于glibc的内置函数int __builtin_popcount (unsigned int n)
      

    • 该算法使用一个计数器ones记录数位1的数目，其初始值为0。随后进入一个循环：通过二进制位的与（and）运算，检查n的二进制展开的最低位，若该位为1则累计至ones。由于每次循环都将n的二进制展开右移一位，故整体效果等同于逐个检验所有数位是否为1。
  • 复杂度
    • 根据右移运算的性质，每右移一位，n都至少缩减一半。也就是说，至多经过 $1+\lfloor log_2n \rfloor$次循环，n必然缩减至0，从而算法终止。实际上从另一角度来看， $1+\lfloor log_2n \rfloor$恰为n二进制展开的总位数，每次循环都将其右移一位，总的循环次数自然也应是 $1+\lfloor log_2n \rfloor$。
    • 由大O记号定义，在用函数 $log_rn$界定渐进复杂度时，常底数 $r$的具体取值无所谓，故通常不予专门标出而笼统地记作logn。此类算法称作具有“对数时间复杂度”（logarithmic-time algorithm）。
    • 更一般地，凡运行时间可以表示和度量为T(n) = O( $log^cn$)形式的这一类算法（其中常数c >0），均统称作“对数多项式时间复杂度的算法（polylogarithmic-time algorithm）。
    • 此类算法的效率虽不如常数复杂度算法理想，但从多项式的角度看仍能无限接近于后者，故也是极为高效的一类算法。

• 线性O(n)

  • 问题与算法

    • 考查如下问题：计算给定n个整数的总和。
    • 数组元素求和算法sumI() ：

      int sumI(int A[], int n)	//数组求和算法（迭代版）
      {
      	int sum = 0;	//初始化累计器，O(1)
      	for (int i = 0; i < n; i++)		//对全部共O(n)个元素求和 
      		sum += A[i];	//累计，O(1)
      	return sum;		//返回累计值，O(1)
      }	// O(1) + O(n)*O(1) + O(1) = O(n+2) = O(n)
      

  • 复杂度

    • 首先，对s的初始化需要O(1)时间。
    • 算法的主体部分是一个循环，每一轮循环中只需进行一次累加运算，这属于基本操作，可在O(1)时间内完成。
    • 每经过一轮循环，都将一个元素累加至s，故总共需要做n轮循环，于是该算法的运行时间应为：O(1) + O(1)*n = O(n + 1) = O(n)
    • 凡运行时间可以表示和度量为T(n) = O(n)形式的这一类算法，均统称作“线性时间复杂度算法” （linear-time algorithm）。
    • 也就是说，对于输入的每一单元，此类算法平均消耗常数时间。就大多数问题而言，在对输入的每一单元均至少访问一次之前，不可能得出解答。以数组求和为例，在尚未得知每一元素的具体数值之前，绝不可能确定其总和。故就此意义而言，此类算法的效率亦足以令人满意。
    • 若运行时间可以表示和度量为T(n) = O(f(n))的形式，而且f(x)为多项式，则对应的算法称作“多项式时间复杂度算法” （polynomial-time algorithm）。
    • 多项式级的运行时间成本，在实际应用中一般被认为是可接受的或可忍受的。 某问题若存在一个复杂度在此范围以内的算法，则称该问题是可有效求解的或易解的（tractable） 。

• 指数O( $2^n$)

  • 问题与算法
    • 考查如下问题：在禁止超过1位的移位运算的前提下，对任意非负整数n，计算幂 $2^n$。
    • 幂函数算法（ 蛮力迭代版）

      __int64 power2BF_I(int n) 
      {	//幂函数2^n算法（蛮力迭代版），n >= 0
      	__int64 pow = 1;	//O(1)：累积器初始化为2^0
      	while ((n --) > 0)	//O(n)：迭代n轮
      	    pow <<= 1;	    //O(1)：将累积器翻倍
      	return pow;	//O(1)：返回累积器
      }	//O(n) = O(2^r)，r为输入指数n的比特位数
      

  • 复杂度
    • 算法power2BF_I()由n轮迭代组成，各需做一次累乘和一次递减，均属于基本操作，故整个算法共需O(n)时间。
    • 若以输入指数n的二进制位数 $r = 1+\lfloor log_2n \rfloor$作为输入规模，则运行时间为O( $2^r$)。
    • 一般地，凡运行时间可以表示和度量为T(n) = O( $a^n$)形式的算法（ a > 1），均属于“指数时间复杂度算法”（exponential-time algorithm）。
    • 当问题规模较大后，指数复杂度算法的实际效率将急剧下降，计算时间之长很快就会达到令人难以忍受的地步。因此通常认为，指数复杂度算法无法真正应用于实际问题中，它们不是有效算法，甚至不能称作算法。相应地，不存在多项式复杂度算法的问题，也称作难解的（intractable）问题。

• 复杂度层次

  • 利用大O记号，不仅可以定量地把握算法复杂度的主要部分，而且可以定性地由低至高将复杂度划分为若干层次。
  • 典型的复杂度层次包括 $O(1)、O(log^*n)、O(loglogn)、O(logn)、O(sqrt(n))、 O(n)、O(nlog^*n)、O(nloglogn)、O(nlogn)、O(n^2)、 O(n^3)、O(n^c)、O(2^n)。$
  • 下图(1)~(7)依次为： $O(logn)、O(\sqrt n)、O(n)、O(nlogn)、 O(n^2)、O(n^3)和O(2^n)。$
    

• 输入规模

  • 对算法复杂度的界定， 都是相对于问题的输入规模而言的。
  • 不同的人在不同场合下关于“输入规模” 的理解、 定义和度量可能不尽相同，因此也可能导致复杂度分析的结论有所差异。
  • 严格地说，所谓待计算问题的输入规模，应严格定义为“用以描述输入所需的空间规模”。