Leetcode Week8 Best Time to Buy and Sell Stock II

Question

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
             Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.

Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Answer

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int maxprofit = 0;
        if (prices.size() == 0) return maxprofit;
        for (int i = 1; i < prices.size(); i++) {
            if (prices[i-1] < prices[i]) {
                maxprofit += prices[i] - prices[i-1];
            } 
        }
        return maxprofit;
    }
    
};

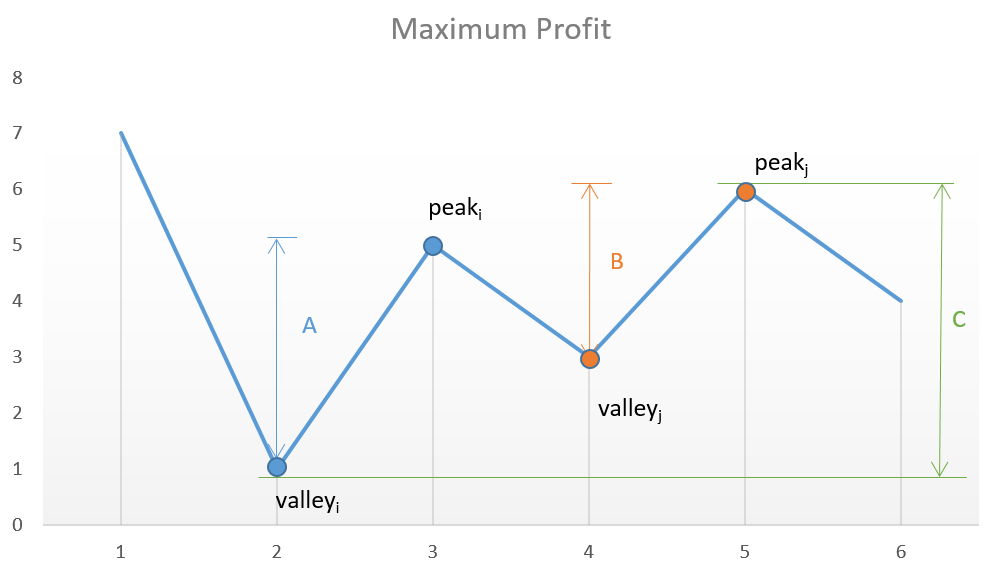
TotalProfit=∑i​(height(peaki​)−height(valleyi​))

在上述情况下,如果我们跳过peak_i 和valley_j试图获得更多的利润考虑分更多的高度不同,获得的净利润将永远比他们获得的较小,因为C总是会比A + B较小。所以只需要见到局部极小值就买入，之后遇到局部极大值就卖出，以上算法就采取该策略。