D. Tree
time limit per test
2 seconds
memory limit per test
512 megabytes
input
standard input
output
standard output
You are given a node of the tree with index 1 and with weight 0. Let cnt be the number of nodes in the tree at any instant (initially, cnt is set to 1). Support Q queries of following two types:
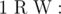Add a new node (index cnt + 1) with weight W and add edge between node R and this node.
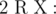Output the maximum length of sequence of nodes which
- starts with R.
- Every node in the sequence is an ancestor of its predecessor.
- Sum of weight of nodes in sequence does not exceed X.
- For some nodes i, j that are consecutive in the sequence if i is an ancestor of j then w[i] ≥ w[j] and there should not exist a node k on simple path from i to j such that w[k] ≥ w[j]
The tree is rooted at node 1 at any instant.
Note that the queries are given in a modified way.
Input
First line containing the number of queries Q (1 ≤ Q ≤ 400000).
Let last be the answer for previous query of type 2 (initially last equals 0).
Each of the next Q lines contains a query of following form:
- 1 p q (1 ≤ p, q ≤ 1018): This is query of first type where
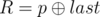and 
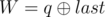. It is guaranteed that 1 ≤ R ≤ cnt and 0 ≤ W ≤ 109. - 2 p q (1 ≤ p, q ≤ 1018): This is query of second type where 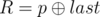and
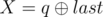. It is guaranteed that 1 ≤ R ≤ cnt and 0 ≤ X ≤ 1015.
denotes bitwise XOR of a and b.
It is guaranteed that at least one query of type 2 exists.
Output
Output the answer to each query of second type in separate line.
Examples
Input
Copy
6
1 1 1
2 2 0
2 2 1
1 3 0
2 2 0
2 2 2
Output
Copy
0
1
1
2
Input
Copy
6
1 1 0
2 2 0
2 0 3
1 0 2
2 1 3
2 1 6
Output
Copy
2
2
3
2
Input
Copy
7
1 1 2
1 2 3
2 3 3
1 0 0
1 5 1
2 5 0
2 4 0
Output
Copy
1
1
2
Input
Copy
7
1 1 3
1 2 3
2 3 4
1 2 0
1 5 3
2 5 5
2 7 22
Output
Copy
1
2
3一开始只有一个点，编号为1，权值为0
接下来有两种操作(last为上一个输出操作输出的值，初始为0)
cnt表示当前的点的数量
1 p q:建立一个新的点，编号为cnt+1,
,然后在点R与cnt+1连一条边，点cnt+1的权值为X，cnt++
2 p q:
,以R为序列开头，找最长的序列满足下述条件
1.序列后面的点是序列前面的点的祖先
2.序列所有点的权值和不超过X
3.序列中顺序a,b，b一定是第一个权值大于等于a的权值的祖先。即不存在b-->a的路径中有点权值>=a
输出这个长度
解析:
这道题真的做了一天.....
一开始想到倍增，但是只能求不考虑第二个条件的最长的序列。后来发现有点问题..看了题解..豁然开朗。。
再建一颗树就好了，再用一遍树上倍增....
官方题解
简单解释一下就是用树上倍增的思想来加速操作。
首先第一颗树就是本身题意的树，这颗树用树上倍增维护第2^j个父亲节点和到2^j个父亲路径上的最大值(不包括起始点)
这个我们就可以求出来用类似LCA的想法求出第一个>=当前点cnt的的点pre
然后第二颗树，我们将cnt与pre连边，表示cnt的最优子序列的后一个点就是pre
因为这个序列是有后缀递推的性质的，所以树上的每一条链都是链上的点的最优序列。
那么此时我们用第二个树上倍增维护第2^j个父亲节点和到2^j个父亲路径上的权值和
我们再用类似LCA的方法求出cnt出发最远的路径终点，使得路径权值和<X
即就是求sum[cnt][1..max]中第一个<X的对应的点
通过这道题其实树上倍增有点类似树上面的ST表/单调队列
对于在x的树链上求第一个大于(小于/不大于/...)都可以用树上倍增来做。
譬如上面第一个求第一个大于等于cnt的，我们可以先找出最远的那点权值<w[cnt]
然后返回找到的那个点的第一个父亲pre，这个点就是第一个>=w[cnt]的点
树上倍增是通过缩小幂来不断迫近答案，可能有点类似线段树
但是记住他还有树链的结构，一般只先考虑靠近x的XX[x][j-1]这个区间。
并且注意XX[x][j-1]一般都表示(x,x的2^j-1个父亲]这条路径
其实这个用二进制来优化的思想也是很重要的，有时候你可能不知道用
树上倍增，但是当想到用logn的算法或者二进制优化的时候就可以想到树上倍增
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 4e5+10;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int fa[N][20];
int max_val[N][20];
int cnt;
int max0;
ll a[N];
int nxt[N][20];
ll sum[N][20]; //sum[i][j]=(i,i的第2^j个父亲]
int dep[N];
void calfather(int x)
{
for(int i=1;i<=max0;i++)
if(fa[x][i-1]) //在dfs(x)之前，x的父辈们的fa数组都已经计算完毕，所以可以用来计算x
{
fa[x][i]=fa[fa[x][i-1]][i-1];
max_val[x][i]=a[max_val[x][i-1]]>=a[max_val[fa[x][i-1]][i-1]]?max_val[x][i-1]:max_val[fa[x][i-1]][i-1];
}
else break; //如果x已经没有第2^(i-1)个父亲了，那么也不会有更远的父亲，直接break
}
int LCA(int u)
{
int ans=0;
for(int x=max0;x>=1;x--) //注意！此处循环必须是从大到小!因为我们应该越提越“精确”，
{
if(fa[u][x-1]) {
/*if (a[max_val[u][x - 1]] >= a[cnt]) {
ans = max_val[u][x - 1];
} else if (a[max_val[fa[u][x - 1]][x - 1]] >= a[cnt]) {
ans = max_val[fa[u][x - 1]][x - 1];
u = fa[u][x - 1];
}else {
break;
}*/
if(a[max_val[u][x - 1]]<a[cnt]) //!!!!!!!!
u=fa[u][x - 1];
}
}
//return ans;
return fa[u][0];
}
void new_calfather(int x)
{
for(int i=1;i<=max0;i++)
if(nxt[x][i-1]) //在dfs(x)之前，x的父辈们的fa数组都已经计算完毕，所以可以用来计算x
{
nxt[x][i]=nxt[nxt[x][i-1]][i-1];
sum[x][i]=sum[x][i-1]+sum[nxt[x][i-1]][i-1];
}
else break; //如果x已经没有第2^(i-1)个父亲了，那么也不会有更远的父亲，直接break
}
int new_LCA(int u,ll X)
{
X-=a[u];
if(X<0) return -1;
for(int x=max0;x>=1;x--) //注意！此处循环必须是从大到小!因为我们应该越提越“精确”，
{
if(nxt[u][x-1]) {
if (sum[u][x-1] <=X ) {
X-=sum[u][x-1];
u = nxt[u][x - 1];
}
}
}
return u;
}
int main()
{
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int n;
scanf("%d",&n);
ll last=0;
cnt=1;
max0=19;
dep[0]=0;
dep[1]=1;
for(int i=0;i<n;i++)
{
int mode;
ll p,q;
scanf("%d%lld%lld",&mode,&p,&q);
p^=last;
q^=last;
if(mode==1)
{
++cnt;
fa[cnt][0]=p;
a[cnt]=q;
max_val[cnt][0]=p;
calfather(cnt);
int pre=LCA(cnt);
nxt[cnt][0]=pre;
dep[cnt]=dep[pre]+1;
sum[cnt][0]=a[pre];
new_calfather(cnt);
}
else
{
int pre=new_LCA(p,q);
if(pre==-1) last=0;
else last=dep[p]-dep[pre]+1;
printf("%lld\n",last);
}
}
}