17. 正则化——解决线性回归模型过拟合问题

版权声明：转载请注明来源及作者，谢谢！ https://blog.csdn.net/qq_42442369/article/details/86511101

多项式扩展时，并不是阶数越多越好

通过之前的程序，我们发现，使用多项式扩展完美的解决了欠拟合问题。如果我们使用更多阶的多项式扩展，甚至可以将拟合度提高为1。但是，问题来了，多项式扩展时，是否阶数越多越好呢？

程序证明

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False

# 定义产生数据规则的函数。（根据x计算y值的函数）
def true_fun(X):
    return np.cos(1.5 * np.pi * X)

np.random.seed(0)
# 生成样本的数量。
n_samples = 30
# 定义不同的多项式阶数，并观察，不同的阶数扩展，会带来怎样的效果。
degrees = [1, 4, 10, 15]

# 随机生成30个样本数据（训练数据）
x_train = np.sort(np.random.rand(n_samples))
# 根据x计算y值。并加入噪声。
y_train = true_fun(x_train) + np.random.randn(n_samples) * 0.1
# 将训练数据由一维扩展到二维。
X_train = x_train[:, np.newaxis]

plt.figure(figsize=(18, 10))
for i, n in enumerate(degrees):
    # 注意：subplot指定的子绘图区域索引，从1开始。
    plt.subplot(2, 2, i + 1)
    pipeline = Pipeline([("poly", PolynomialFeatures(degree=n)), 
            ("lr", LinearRegression())])
    pipeline.fit(X_train, y_train)
    train_score = pipeline.score(X_train, y_train)

    x_test = np.linspace(0, 1, 100)
    y_test = true_fun(x_test)
    X_test = x_test[:, np.newaxis]
    test_score = pipeline.score(X_test, y_test)
    plt.plot(X_test, pipeline.predict(X_test), label="预测线")
    plt.plot(X_test, true_fun(X_test), label="真实线")
    plt.scatter(X_train, y_train, c='b', s=20, label="样本数据")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim((0, 1))
    plt.ylim((-2, 2))
    plt.legend(loc="best")
    plt.title(f"训练集：{train_score:.3f} 测试集：{test_score:.3f}")
    # 通过流水线获取线性回归类的对象，然后输出权重值。
    print(pipeline.named_steps["lr"].coef_)
plt.show()

解释

定义产生数据规则的函数，就是计算y值
想产生一个类似 余弦函数
需要用到索引，子绘图区域用
看完训练集，再看测试集

注意测试集没有加噪音

物极必反，模型复杂度太高
最后一个图，定义了高达15阶，模型打分特别差。

引入正则化

练习

我们将之前的程序中，输入系数（权重与偏置）的注释取消，再次运行程序，我们会发现什么？

上图有什么规律？
绝对值越来越大，权重越来越大，只要x越大 y变化特别大
W值不能太大，太大就会出现过拟合，虽然能够找到损失函数最小值

所以用一个权重的惩罚项

抑制住，不让w过大

W=400 最好 损失函数 400 + 100 因为就算前面很小，后面也会很大
Why权值抑制？
因为权值太大 过拟合

Fw 权值越大 fw越大，所以以前最优的w就不是最优
以前w不大的话，没关系
但是w很大的话，相加的话就不是最大的了

3种正则化说明

在线性回归中，模型过于复杂，通常表现为模型的参数过大（指绝对值过大），即如果模型的参数过大，就容易出现过拟合现象。我们可以通过正则化来降低过拟合的程度。正则化，就是通过在损失函数中加入关于权重的惩罚项，进而限制模型的参数过大，从而减低过拟合，增加的惩罚项，我们也称作正则项。
根据正则项的不同，我们可以将正则化分为如下几种：

• L2正则化
• L1正则化
• Elastic Net

L2正则化

L2正则化是最常使用的正则化，将所有权重的平方和作为正则项。使用L2正则的线性回归模型称为Ridge回归（岭回归）。加入L2正则化的损失函数为：
$J(w) = \frac{1}{2}\sum_{i=1}^{m}(y ^ {(i)} - \hat{y} ^ {(i)}) ^ 2 + \alpha \sum_{j=1}^{n}w_{j} ^ {2}$

从包含正则项的损失函数中，我们可以发现，我们将损失函数分为两部分，一部分为原来的损失函数，另外一部分为正则项的惩罚，这样，如果当权重过大时，即使原来的损失函数值很小，但是整个项的损失值会很多，因此，整个损失值（二者的和）也不会很小，从而，权重过大的w就可能不会成为最佳解。

L1正则化

L1正则化使用所有权重的绝对值和作为正则项。使用L1正则的线性回归模型称为LASSO回归（Least Absolute Shrinkage and Selection Operator——最小绝对值收缩与选择因子）。
$J(w) = \frac{1}{2}\sum_{i=1}^{m}(y ^ {(i)} - \hat{y} ^ {(i)}) ^ 2 + \alpha \sum_{j=1}^{n}|w_{j}|$

Elastic Net

Elastic Net（弹性网络），同时将绝对值和与平方和作为正则项，是L1正则化与L2正则化之间的一个折中。使用该正则项的线性回归模型成为Elastic Net算法。

$J(w) = \frac{1}{2}\sum_{i=1}^{m}(y ^ {(i)} - \hat{y} ^ {(i)}) ^ 2 + \alpha(p\sum_{j=1}^{n}|w_{j}| + (1 - p)\sum_{j=1}^{n}w_{j} ^ {2})$

说明：
以上假设样本数量为m，特征数量为n。
$\alpha > 0$并且 $0 <= p <= 1$

L2 用什么代表惩罚项
都有α 相当于惩罚系数
不是用的平方和，而是绝对值和
Elastic Net相当于L1和l2的综合

α月越来越大 ，我们一定要把权值变得很小很小,，否则jw就不是最优解，前面数量积越来越小，后面的数量积越来越大，后面项占有的地位越来越重要

α越来越小，权值哪怕很小，后面项几乎没有用，不重要

程序解释

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
# 线性回归使用L2正则化项，就称为岭回归。
from sklearn.linear_model import Ridge
mpl.rcParams["font.family"] = "serif"
mpl.rcParams["axes.unicode_minus"] = False

X, y, w = make_regression(n_samples=10, n_features=10, coef=True,
        random_state=1, bias=3.5)

# 选择200个不同的alpha值，进而演示，在不同的alpha参数作用下，w会有这怎样的变化。
# 即alpha值的不同，对w的影响。
alphas = np.logspace(-4, 4, 200)
# 定义权重（系数）列表，用来存储每个不同的alpha取值时，对应的权重是多少。
coefs = []
# 创建Ridge回归类的对象。
ridge = Ridge()
for a in alphas:
    # 设置alpha参数的值。
    ridge.set_params(alpha=a)
    ridge.fit(X, y)
    # 使用权重加入每个不同的alpha训练之后，模型的w值。
    coefs.append(ridge.coef_)

# 获取当前的绘图区域对象。
ax = plt.gca()
# 注意：coefs是一个二维数组结构，我们将其作为y进行绘制的时候，
# 会将每一列绘制出一条线，因此，具有10条线。
ax.plot(alphas, coefs)
# 设置x轴刻度为log。即以对数级的形式进行表示。
ax.set_xscale('log')
ax.set_xlabel('alpha')
ax.set_ylabel('weights')

Gca
多演示一种
Plt直接也可以
设置轴刻度为Log why log???
每个线就是一个权重 每个特征feature就是一个权重
在α不同取值下，a很小，不影响权重，当值很大的时候，惩罚力度越来越大，损失最大，w权重接近于0

Why一个plot 10条线？
Dataf 有几列，就有几条线
因为coef是二维的

200 个值就有一个趋势

1 4 3是一条线 每一列是一条线，二维的结构

这里面有200行 10列

所以可以画出10条线

不同的正则化之间的比较

• L2正则化不会产生稀疏解，L1正则化会产生稀疏解，这也使得LASSO成为一种监督特征选择技术。
• 如果数据的维度中存在噪音和冗余，稀疏的解可以找到有用的维度并且减少冗余，提高回归预测的准确性和鲁棒性。
• Ridge模型具有较高的准确性、鲁棒性以及稳定性，而LASSO模型具有较高的求解速度。
• 如果既要考虑稳定性也考虑求解的速度，可考虑使用Elasitc Net。

L2正则化，不会产生稀疏解

相切的点，最优，两个之和
因为是切点 产生不了稀疏解
L1能

切到○上 w1 w2都不是0 不是稀疏解

L1 正则化 找最优解的话 是菱形和○相切 的点有稀疏解
L2 正则化 找最优解的话 ○和○相切 的点 没稀疏解 w1 ww2 不为0

不一定是○

弹性网络含有喜树街

加上正则项，付出的代价，损失值增大，换来的的
换来的好处是减少过拟合，在未知数据集上表现的更好

偏差 ： 损失值

方差 ： 训练的 测试的损失读 减少训练集和测试集的差距

偏置 数学上的截距
噪声 真实数据上的

增加了偏差
减少了方差

差异之处程序解释

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet

mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False

def true_fun(X):
    return np.cos(1.5 * np.pi * X)

np.random.seed(0)
n_samples = 30

x_train = np.sort(np.random.rand(n_samples))
y_train = true_fun(x_train) + np.random.randn(n_samples) * 0.1
X_train = x_train[:, np.newaxis]

# 定义各种模型
models = [("线性回归（无正则化）", LinearRegression()), ("L1正则化：", Lasso(alpha=0.01)), 
         ("L2正则化", Ridge(alpha=0.01)), ("弹性网络", ElasticNet(alpha=0.01, l1_ratio=0.5))]
plt.figure(figsize=(18, 10))
for i, (name, model) in enumerate(models):
    plt.subplot(2, 2, i + 1)
    pipeline = Pipeline([("poly", PolynomialFeatures(degree=15)), ("model", model)])
    pipeline.fit(X_train, y_train)
    train_score = pipeline.score(X_train, y_train)

    x_test = np.linspace(0, 1, 100)
    y_test = true_fun(x_test)
    X_test = x_test[:, np.newaxis]
    test_score = pipeline.score(X_test, y_test)
    plt.plot(X_test, pipeline.predict(X_test), label="预测线")
    plt.plot(X_test, true_fun(X_test), label="真实线")
    plt.scatter(X_train, y_train, c='b', s=20, label="样本数据")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim((0, 1))
    plt.ylim((-2, 2))
    plt.legend(loc="best")
    plt.title(f"{name} 训练集：{train_score:.3f} 测试集：{test_score:.3f}")
    print(pipeline.named_steps["model"].coef_)
plt.show()

元祖
创 流水线
流水线fit

训练好后，看得分

L1 lasso 缓解了过拟合
再也不是过渡的震荡
牺牲了训练集上的打分，测试集表现很好

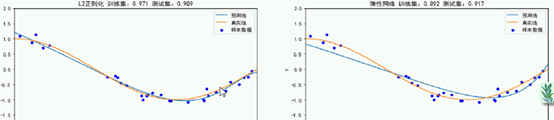
尽管训练集上 性能 降低

可以看到 0 产生 ，L1 稀疏解

不让权重变得很大，同时抑制

实际中 把多项式扩展调小一点就行了
这里要说的就是 正则化可以解决过拟合的问题