数字信号处理相关8（傅立叶变换、拉普拉斯变换、Z变换的联系？）

来自：https://www.zhihu.com/question/22085329

第一次回答一个跟自己的专业相关的题目。

首先，为什么要进行变换？因为很多时候，频率域比时域直观得多。

傅里叶级数和傅里叶变换，表明时域的信号可以分解为不同频率的正弦波的叠加。而如果我们把两个没有公共频率成分的信号相加，一同发送。在接收端接收到之后，用滤波器把两个信号分开，就可以还原出发送的两个信号。这就是通信过程的实质。

而在这个过程中，发送端发送出去的信号的最大频率和最小频率是否在接收端的带通滤波器的上下边界频率之内？如果超出了滤波器的频率范围，接收端接收到的信号就会丢失一部分信息，接收端接收到的消息就会有错误。

但这个问题从时域是很难看出来的，不过，从频率域就一目了然。

因此傅里叶变换得到了广泛应用，它的地位也非常重要。

然而，可以进行傅里叶变换的信号似乎不那么够用，傅里叶变换的收敛有一个狄利克雷条件，要求信号绝对可积/绝对可和。
为了使不满足这一条件的信号，也能读出它的“频率”，拉普拉斯变换和Z变换，对“频率”的含义做出了扩充，使得大多数有用信号都具有了对应的“频率”域表达式，方便了对各个器件的设计。

=====================================

接下来一个问题，傅氏变换、拉氏变换、Z变换之间到底有什么关系？

首先，傅里叶变换粗略分来包括连续时间傅里叶变换（CTFT）、离散时间傅里叶变换（DTFT）。
CTFT是将连续时间信号变换到频域，将频率的含义扩充之后，就得到拉普拉斯变换。
DTFT是将离散时间信号变换到频域，将频率的含义扩充之后，就得到Z变换。

这里解释一下，很多教材对于频率的含义没有明确规定，由于CTFT和DTFT的形式分别为 $X\left( j\omega \right)$ 和 $X\left( e^{j\omega} \right)$ ，因此很多人误将频率理解为 $j\omega$ 和 $e^{j\omega}$ 。
但事实上我们在绘制频谱图的时候，取的自变量都是 $\omega$ ，这样才能画出函数图像。否则CTFT和DTFT都将变成复平面上变化的函数，无法画出函数图像了。
而且我们日常用到频率这一概念时所说的 $f$ ，都是 $f=\frac{\omega}{2\pi}$ .其对应的角频率恰恰是实数 $\omega$ ，而不是复数 $j\omega$ 或 $e^{j\omega}$ 。
因此，我们所说的频率指的应当是 $\omega$ 而不是 $j\omega$ 或 $e^{j\omega}$ 。

1、连续时间傅里叶变换与拉普拉斯变换的关系
连续时间傅里叶变换的公式是： $\int_{-\infty}^{\infty } x(t)e^{-j\omega t} dt$ ，这里的 $\omega$ 是实数。
傅里叶变换要求时域信号绝对可积，即 $\int_{-\infty }^{\infty } \left| x(t) \right| dt<\infty$ 。
为了让不符合这个条件的信号，也能变换到频率域，我们给x(t)乘上一个指数函数 $e^{-\sigma t}$ ， $\sigma$ 为（满足收敛域的）任意实数。
可以发现， $x(t)e^{-\sigma t}$ 这个函数，就满足了绝对可积的条件，即 $\int_{-\infty }^{\infty } \left| x(t)e^{-\sigma t} \right| dt<\infty$ 。

关于为什么 $x\left( t \right)e^{-\sigma t}$ 满足绝对可积条件，这里提一下，感性地说，我们知道负指数函数随t的增大，趋于零的速度是所有函数中最快的，这也是为什么我们描述某个现象暴涨的时候会说指数上升。因此大多数一般的函数 $x\left( t \right)$ 乘上某个负指数函数之后，一定绝对可积。
用更加严谨的数学表达，对于大多数 $x(t)$ ， $\exists \sigma\in \Re$ ，使得 $\lim_{t \rightarrow \infty}{e^{-\sigma t}}$ 是 $\lim_{t \rightarrow \infty}{x\left( t \right)}$ 的高阶无穷小。即 $\lim_{t \rightarrow \infty}{\frac{e^{-\sigma t}}{x\left( t \right)}}=0$ 。因此在 $e^{-\sigma t}$ 的压迫下， $x(t)e^{-\sigma t}$ 就满足了绝对可积的条件。后文DTFT中的绝对可和条件与此类似，后文不再赘述。

于是这个新函数的傅立叶变换就是： $\int_{-\infty }^{\infty } x(t)e^{-\sigma t} e^{-j\omega t} dt$ ，
化简得 $\int_{-\infty }^{\infty } x(t)e^{-(\sigma +j\omega )t}$ 。
显然 $\sigma +j\omega$ 是一个复数，我们把这个复数定义为一个新的变量——复频率，记为s。
于是便得到了拉普拉斯变换的公式： $\int_{-\infty }^{\infty } x(t)e^{-st} dt$

拉普拉斯变换解决了不满足绝对可积条件的连续信号，变换到频率域的问题，同时也对“频率”的定义进行了扩充。
所以拉普拉斯变换与连续时间傅里叶变换的关系是：
拉普拉斯变换将频率从实数推广为复数，因而傅里叶变换变成了拉普拉斯变换的一个特例。
当s为纯虚数时，x(t)的拉普拉斯变换，即为x(t)的傅里叶变换。

从图像的角度来说，拉普拉斯变换得到的频谱是一个复平面上的函数，（为方便作图，这里只给出了拉氏变换的幅度谱和傅氏变换的幅度谱的关系。相位谱具有类似的关系。）

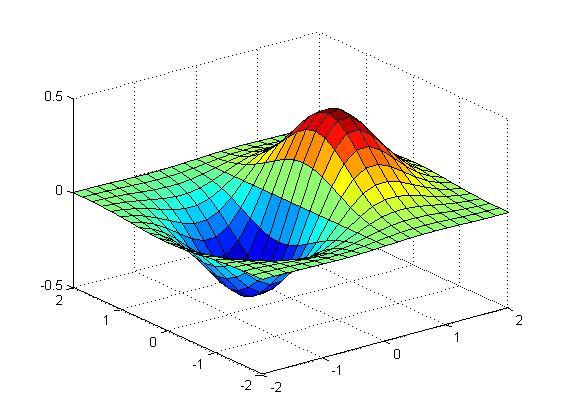
而傅里叶变换得到的频谱，则是从虚轴上切一刀，得到的函数的剖面。

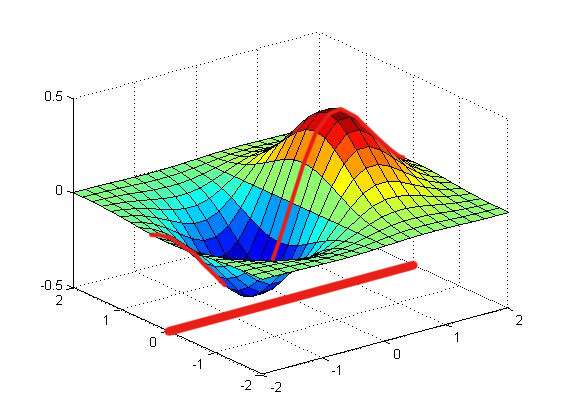
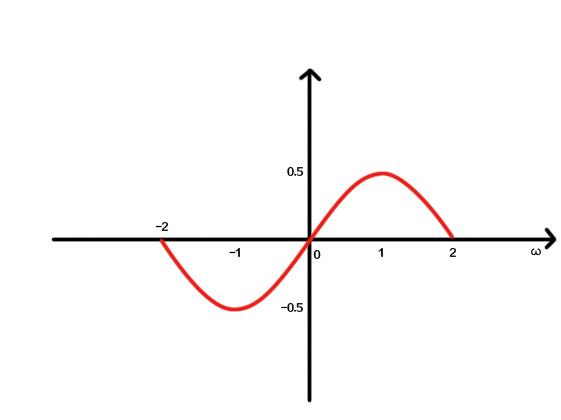
2、离散时间傅里叶变换（DTFT）与Z变换的关系
DTFT的公式是 $\sum_{n=-\infty }^{\infty }{x[n]e^{-j\omega n} }$ ，这里的 $\omega$ 是连续变化的实数。
同样的，DTFT需要满足绝对可和的条件，即 $\sum_{n=-\infty }^{\infty }{\left| x[n] \right| } <\infty$ 。
为了让不满足绝对可和条件的函数x[n]，也能变换到频率域，我们乘一个指数函数 $a^{-n}$ ， $a$ 为（满足收敛域的）任意实数。
则函数 $x[n]a^{-n}$ 的DTFT为： $\sum_{n=-\infty }^{\infty }{x[n]a^{-n}e^{-j\omega n} }$ ，
化简得： $\sum_{n=-\infty }^{\infty }{x[n](a\cdot e^{j\omega })^{-n} }$
显然， $a\cdot e^{j\omega }$ 是一个极坐标形式的复数，我们把这个复数定义为离散信号的复频率，记为z。
则得到Z变换的公式： $\sum_{n=-\infty }^{\infty }{x[n]z^{-n} }$ 。

关于这里为什么对x[n]乘以 $a^{-n}$ 而不是像拉氏变换中乘以 $e^{-\sigma n}$ ，主要是由离散序列的DTFT的周期性决定的。如果对离散序列进行拉氏变换，将 $\omega$ 映射到虚轴上，则得到的变换函数是在虚轴方向上周期变化的函数，这样就没有充分利用DTFT的周期性。
而Z变换令 $z=a\cdot e^{j\omega}$ ，则当a=1，即 $z=e^{j\omega}$ 时，随着 $\omega$ 从 $-\infty$ 向 $+\infty$ 变化，z在复平面中的单位圆上以 $2\pi$ 为周期变化，如此恰能充分利用DTFT的周期性进一步简化我们的计算。

Z变换解决了不满足绝对可和条件的离散信号，变换到频率域的问题，同时也同样对“频率”的定义进行了扩充。
所以Z变换与离散时间傅里叶变换（DTFT）的关系是：
Z变换将频率从实数推广为复数，因而DTFT变成了Z变换的一个特例。
当z的模为1时，x[n]的Z变换即为x[n]的DTFT。

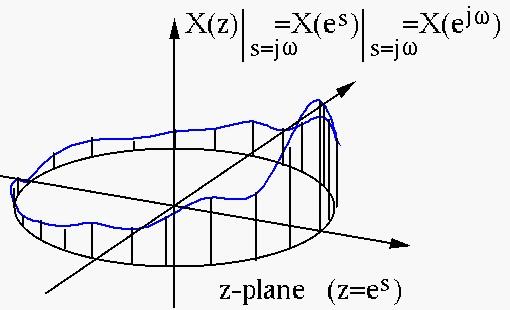
从图像的角度来说，Z变换得到的频谱，是一个复平面上的函数，而DTFT得到的频谱，则是沿着单位圆切一刀，得到的函数的剖面，从负实轴切断展开的图像。（为方便作图，这里只给出了Z变换的幅度谱和傅氏变换的幅度谱的关系。相位谱具有类似的关系。）

数字信号处理相关8（傅立叶变换、拉普拉斯变换、Z变换的联系？）

猜你喜欢