文章目录

1.为什么要激活函数
2.常见激活函数

2.1.sigmoid激活函数
2.2.tanh激活函数
2.3.Relu激活函数
2.4.PRelu

2.4.1.RRelu
2.4.2.Leaky ReLU

2.5.elu激活函数
2.6.Gelu激活函数
2.7.Maxout 激活函数

1.为什么要激活函数

举个例子，首先我们有这个需求，就是二分类问题，如我要将下面的三角形和圆形点进行正确的分类，如下图：在这里插入图片描述
利用我们单层的感知机, 用它可以划出一条线, 把平面分割开：

很容易能够看出，我给出的样本点根本不是线性可分的，一个感知器无论得到的直线怎么动，都不可能完全正确的将三角形与圆形区分出来，单层感知器是一个线性分类器。那么我们很容易想到用多个感知器来进行组合，以便获得更大的分类问题，下面我们上图，看是否可行：
在这里插入图片描述
我们已经得到了多感知器分类器了，那么它的分类能力是否强大到能将非线性数据点正确分类开呢~我们来分析一下：

我们能够得到
$y = w_{2-1}(w_{1-11}x_1+w_{1-21}x2+b_{1-1})+w_{2-2}(w_{1-12}x_1+w_{1-22}x_2+b_{1-2}+w_{2-3}(w_{1-13}x_3+w_{1-23}x_2+b_{1-3})$
我们整理一下：
$y = x_1(w_{2-1}w_{1-11}+w_{2-2}w_{1_12}+w_{2-3}w_{1-13}) + \\ x_2(w_{2-1}w_{1-21}+w_{2-2}w_{1_22}+w_{2-3}w_{1-23}) +x_3(w_{2-1}w_{1-31}+w_{2-2}w_{1_32}+w_{2-3}w_{1-33})$
不管它怎么组合，最多就是线性方程的组合，最后得到的分类器本质还是一个线性方程，该处理不了的非线性问题，它还是处理不了。就好像下图，直线无论在平面上如果旋转，都不可能完全正确的分开三角形和圆形点：
在这里插入图片描述
既然是非线性问题，总有线性方程不能正确分类的地方。
激活函数，神经网络中每一层叠加完了之后，我们需要加入一个激活函数（激活函数的种类也很多，如sigmoid等）这里给出sigmoid例子，如下图：

通过这个激活函数映射之后，输出很明显就是一个非线性函数。
同理，扩展到多个神经元组合的情况时候，表达能力就会更强。
最后再通过优化损失函数的做法，能够学习到不断靠近正确分类三角形和圆形点的曲线。

具体会学到什么曲线，也许是下面这样：
在这里插入图片描述
那么随着不断训练优化，也就能够解决非线性的问题了。

所以到这里为止，我们就解释了这个观点，加入激活函数是用来加入非线性因素的，解决线性模型所不能解决的问题。

2.常见激活函数

2.1.sigmoid激活函数

sigmoid函数为： $S(x) = \frac{1}{1+e^{-x}} = 1- \frac{e^{-x}} {1+e^{-x}}$
一阶导数： $S'(x) = \frac {e^{-x}} {{(1+e^{-x})}^2} = S(x)(1-S(x))$

函数及一阶导数图像：
在这里插入图片描述
特点：

因为其函数值都大于0，因此该函数不是zero-centered
sigmoid在x>>0时，函数值趋近1，在x<<0时，函数值趋近0。另外可以发现函数在两端附近的梯度较小，这也是sigmoid的缺点，在这些x值处，梯度容易饱和，从而造成参数无法更新或者更新很慢。

对应的初始化方法：Xavier

2.2.tanh激活函数

tanh函数： $tanh(x) = \frac {sinh(x)} {cosh(x)} = \frac {e^{x}-e^{-x}} {e^x+e^{-x}}$

函数及一阶导数图像：
在这里插入图片描述
特点：
基本性质同sigmoid没有多少出入，只是将值映射到了[-1,1]这个区间。虽然也是非线性的，依旧有梯度饱和的情况存在，但比sigmoid函数延迟了饱和期。

权重初始化：

2.3.Relu激活函数

Relu函数： $f(x) = \max(0, x)$
函数及一阶函数图像
在这里插入图片描述
函数分析：
这样的一个激活函数对数据会产生什么样的影响呢？注意到， $Wx+b=0$ 是一个超平面，在这个超平面的两侧，x受到了不同的对待： $Wx+b<0$ 的部分，函数值直接被“挤压”至0，而 $Wx+b>0$ 的部分，函数值保持不变，画成图就是：
在这里插入图片描述
下方的数据点被推向横轴，左侧的数据点被推向了纵轴，形成了两条数据非常密集的直线（高维上就是超平面）。注意上图中，两个Wx+b被画成了正交的，通常在一个训练好的神经网络模型中，它们并不是正交的。非正交的情况、高维的情况需要读者自行想象。
上图说明，只有一个象限（抱歉我不知道高维空间里面这个词叫什么，还是就叫象限吧）的信息被保留了，而其他象限的信息被不同程度地压缩了，而且压缩幅度非常大，使其完全无法恢复。这其实是非常不合理的，也许这里仍旧有一些可以加以区分的信息被压缩没了，当然，这些信息在其他卷积核中也许会有所体现，但这样断绝一切可能性的做法并不可取，因此便有了Leaky ReLU的想法。

特点：
ReLu也叫修正线性单元，是一种线性的激活函数。它的提出消除了sigmoid和tanh的梯度饱和的情况，并且其梯度也很好求出。一般现在神经网络的激活函数默认使用ReLu。
sigmoid和tanh是“饱和激活函数”，而ReLU及其变体则是“非饱和激活函数”。使用“非饱和激活函数”的优势在于两点：
1.首先，“非饱和激活函数”能解决所谓的“梯度消失”问题。
2.其次，它能加快收敛速度。
在这里插入图片描述
缺点：

坏死: ReLU 强制的稀疏处理会减少模型的有效容量（即特征屏蔽太多，导致模型无法学习到有效特征）。由于ReLU在x < 0时梯度为0，这样就导致负的梯度在这个ReLU被置零，而且这个神经元有可能再也不会被任何数据激活，称为神经元“坏死”。
无负值: ReLU和sigmoid的一个相同点是结果是正值，没有负值.

权重初始化：
建议使用He Initializer(MSRA Initializer)

tanh sigmoid Relu对比：
可参见The vanishing gradient problem and ReLUs – a TensorFlow investigation

2.4.PRelu

$f(x)=max(αx,x)$
称为Parametric Rectifier(PReLU),将 $α$ 作为可学习的参数.

2.4.1.RRelu

当 α 从高斯分布中随机产生时称为Random Rectifier（RReLU）。

2.4.2.Leaky ReLU

Leaky ReLU函数：
$y=max(0,Wx+b)+\alpha min(0,Wx+b)$
或者 $f(x)=max(αx,x)$
这里的 $\alpha$ 一般固定为 $\alpha = 0.01$
函数图像：
在这里插入图片描述
函数图像跟Relu相似，区别在于小于0的时候，激活后的分布：

函数说明：
当x<0时,f(x)=αx,其中α非常小,这样可以避免在x<0时,不能够学习的情况。
特点：
该函数是对Relu的改进，既起到了修正数据分布的作用，又不一棍打死，在后面几层需要负轴这边信息的时候不至于完全无法恢复。 (其实虽然理论比较合理，但是在实践的时候，对比Relu激活函数并没有起到很大的改进)

2.5.elu激活函数

函数公式：
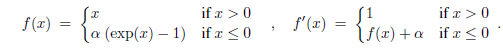
在这里插入图片描述
函数图像：

函数描述：
ELU通过在正值区间取输入x本身减轻了梯度弥散问题（x>0区间导数处处为1），这一点特性这四种激活函数都具备。四者当中只有ReLU的输出值没有负值，所以输出的均值会大于0，当激活值的均值非0时，就会对下一层造成一个bias，如果激活值之间不会相互抵消（即均值非0），会导致下一层的激活单元有bias shift。如此叠加，单元越多时，bias shift就会越大。相比ReLU，ELU可以取到负值，这让单元激活均值可以更接近0，类似于Batch Normalization的效果但是只需要更低的计算复杂度。虽然LReLU和PReLU都也有负值，但是它们不保证在不激活状态下（就是在输入为负的状态下）对噪声鲁棒。反观ELU在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性。

特点：
ELU实现了两个优点：

将前面单元输入的激活值均值控制在0
让激活函数的负值部分也可以被使用了（这意思应该是之前的激活函数，负值部分几乎不携带信息，特别是ReLU），相比relu，elu存在负值，可以将激活单元的输出均值往0推近，达到 batchnormlization的效果且减少了计算量。（输出均值接近0可以减少偏移效应进而使梯
度接近于自然梯度。）

更多详情可以查看详情
更多Relu、elu、prelu比较,显示Relu+batch normal效果是最好的。

2.6.Gelu激活函数

函数公式：
$GELU(x)=xP(X<=x)=xΦ(x)$

这里 $\Phi(x)$ 是正太分布的概率函数，可以简单采用正太分布 $\N(0,1)$ , 要是觉得不刺激当然可以使用参数化的正太分布 $\N(\mu,\sigma)$ , 然后通过训练得到 $\mu,\sigma$ 。

对于假设为标准正太分布的 $GELU(x)$ , 论文中提供了近似计算的数学公式，如下：
$GELU(x)=0.5x(1+tanh[\sqrt{2/π}(x+0.044715x^3)])$
函数图像：
在这里插入图片描述
函数介绍：
领域的鄙视链，在激活函数领域，大家公式的鄙视链应该是：Elus > Relu > Sigmoid ，这些激活函数都有自身的缺陷， sigmoid容易饱和，Elus与Relu缺乏随机因素。

在神经网络的建模过程中，模型很重要的性质就是非线性，同时为了模型泛化能力，需要加入随机正则，例如dropout(随机置一些输出为0,其实也是一种变相的随机非线性激活)，而随机正则与非线性激活是分开的两个事情，而其实模型的输入是由非线性激活与随机正则两者共同决定的。

GELUs正是在激活中引入了随机正则的思想，是一种对神经元输入的概率描述，直观上更符合自然的认识，同时实验效果要比Relus与ELUs都要好。

GELUs其实是 dropout、zoneout、Relus的综合，GELUs对于输入乘以一个0,1组成的mask，而该mask的生成则是依概率随机的依赖于输入。假设输入为X, mask为m，则m服从一个伯努利分布( $\Phi(x)$ , $\Phi(x) = P(X \leq x)$ ,X服从标准正太分布)，这么选择是因为神经元的输入趋向于正太分布，这么设定使得当输入x减小的时候，输入会有一个更高的概率被dropout掉，这样的激活变换就会随机依赖于输入了。
公式中x是自己，P(X<=x)决定x中有多少信息保留，并且由于P是服从高斯分布的，也就满足了非线性的特征，并且更加符合数据的分布预期。

特点：
相比Relu：Relu将小于0的数据映射到0，将大于0的给与等于映射操作，虽然性能比sigmoid好，但是缺乏数据的统计特性，而Gelu则在relu的基础上加入了统计的特性。

源码
该函数出现在了BERT中，在tensorflow 中的实现如下：

def gelu(input_tensor):
	cdf = 0.5 * (1.0 + tf.erf(input_tensor / tf.sqrt(2.0)))
	return input_tesnsor*cdf

感觉bert源码中的近似计算更简单，具体怎么近似的，我猜不出来。

2.7.Maxout 激活函数

Maxout模型实际上也是一种新型的激活函数，在前馈式神经网络中，Maxout的输出即取该层的最大值，在卷积神经网络中，一个Maxout feature map可以是由多个feature map取最值得到。
maxout的拟合能力是非常强的，它可以拟合任意的的凸函数。但是它同dropout一样需要人为设定一个k值。
为了便于理解，假设有一个在第i层有2个节点第（i+1）层有1个节点构成的神经网络。
在这里插入图片描述
激活值 $out = f(W \cdot X+b)$ ; $f$ 是激活函数。 $\cdot$ 在这里代表內积:
$X = (x_1,x_2)^TW = (w_1,w_2)^T$
那么当我们对（i+1）层使用maxout（设定k=5）然后再输出的时候，情况就发生了改变。

此时网络形式上就变成上面的样子，用公式表现出来就是：
$z_1 = W_1 \cdot X+b_1;$
$z_2 = W_2 \cdot X+b_2;$
$z_3 = W_3 \cdot X+b_3;$
$z_4 = W_4 \cdot X+b_4;$
$z_5 = W_5 \cdot X+b_5;$
$out = max(z_1,z_2,z_3,z_4,z_5);$
也就是说第（i+1）层的激活值计算了5次，可我们明明只需要1个激活值，那么我们该怎么办？其实上面的叙述中已经给出了答案，取这5者的最大值来作为最终的结果。
总结一下，maxout明显增加了网络的计算量，使得应用maxout的层的参数个数成k倍增加，原本只需要1组就可以，采用maxout之后就需要k倍了。
再叙述一个稍微复杂点的应用maxout的网络，网络图如下：
在这里插入图片描述
对上图做个说明，第i层有3个节点，红点表示，而第（i+1）层有4个结点，用彩色点表示，此时在第（i+1）层采用maxout（k=3）。我们看到第（i+1）层的每个节点的激活值都有3个值，3次计算的最大值才是对应点的最终激活值。我举这个例子主要是为了说明，决定结点的激活值的时候并不是以层为单位，仍然以节点为单位。
更多参考链接

参考链接：

深度模型之激活函数以及Initializer