数据结构与算法之美（笔记5）排序

如何分析一个排序的算法？

执行效率

内存消耗

如何分析一个排序的算法？

执行效率

最好，最坏，平均时间复杂度
时间复杂度的系数，常数，低阶
比较的次数（或者移动的次数）

内存消耗

原地排序算法：就是特指空间复杂度是O(1)的排序算法。

排序算法的稳定性

如果数据经过某种排序算法排序之后，相同数据之间的位置顺序没有改变，那我们就把这种排序算法叫做稳定的排序算法，如果前后顺序发生了变化，那对应的排序算法就叫作不稳定的排序算法。

冒泡排序

思路：冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系的要求。如果不满足就互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复n次，就完成了n个数据的排序工作。

比如说一组数据4,5,6,3,2,1，从小到大进行排序。

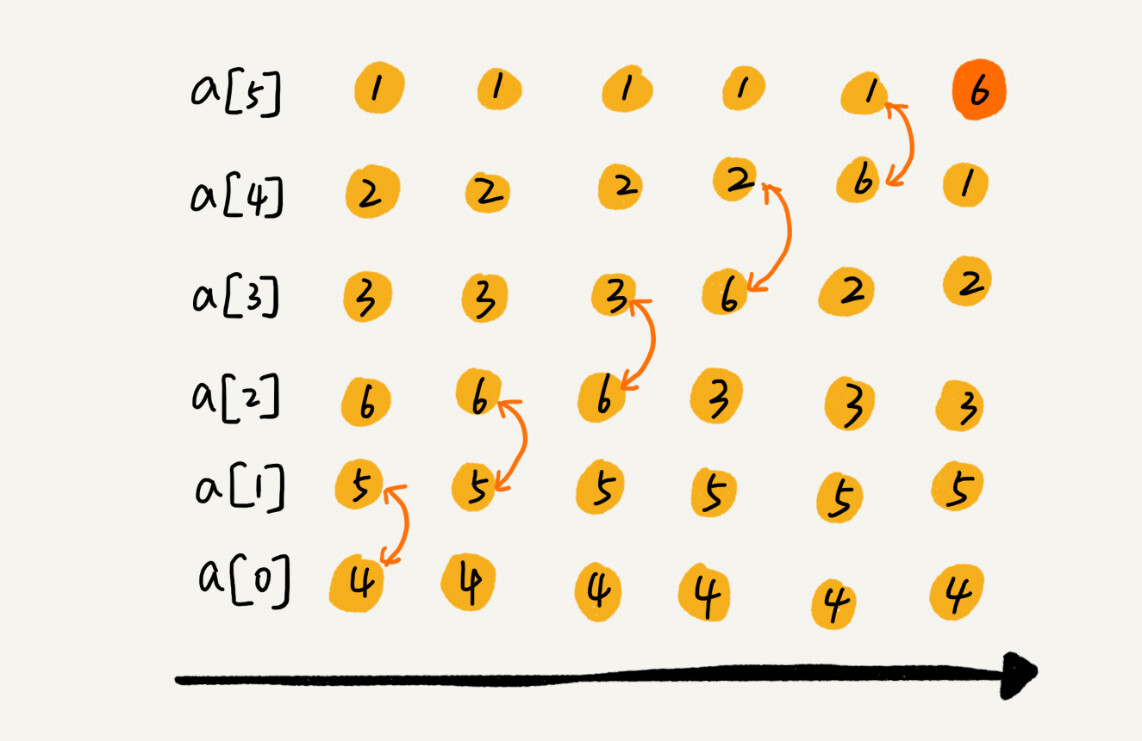
可以看到，经过了一次冒泡操作之后，6这个元素已经存储在正确的位置上了。要想完成所有数据的排序，我们只要进行6次这样的操作就可以了。

但这个还是可以优化的：我们设置一个flag来判断是否有位置交换，一旦没有了位置的交换，那么就说明已经排好序了。

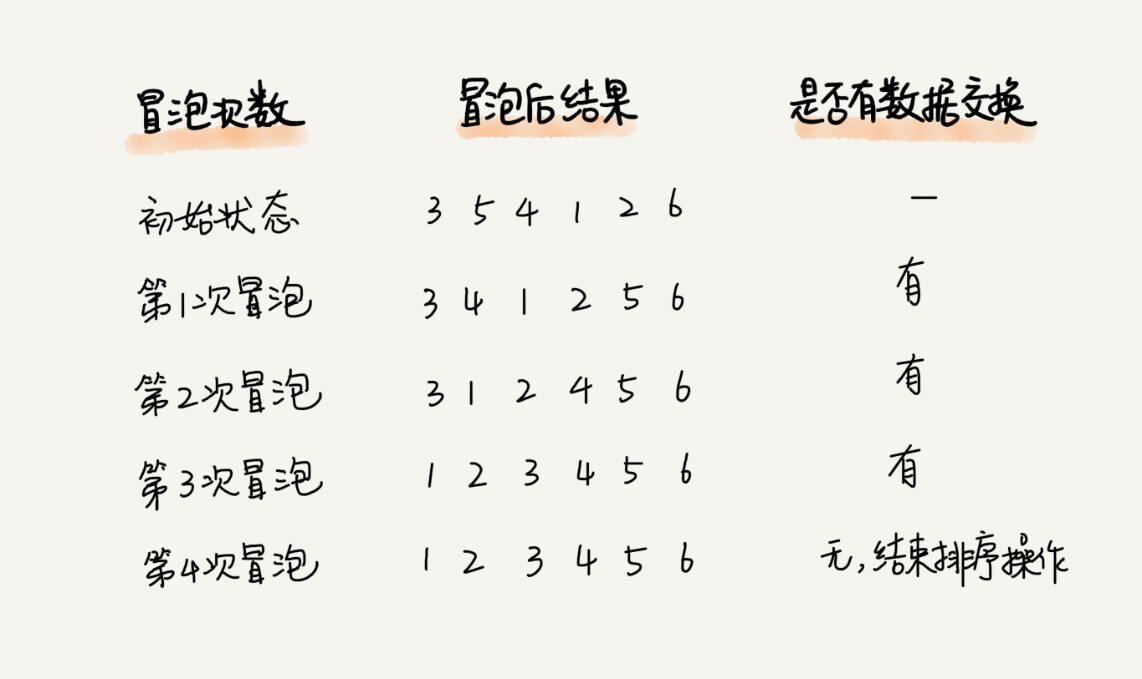
这里给出代码的实现：

void bubble_sort(int* arr,int size){
    if(size <= 1){
        return;
    }
    for(int i=0;i<size;++i){
        bool flag = false;
        for(int j=0;j<size-1-i;++j){
            if(arr[j] > arr[j+1]){
                int temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
                flag = true;
            }
        }
        if(flag == false){
            break;
        }
    }
}

分析：

1.时间复杂度

冒泡排序的最好时间复杂度是O(n)（这个还是优化之后的），最坏时间复杂度是O( $n^{2}$ ),那么平均时间复杂度呢？为了简化分析的过程，我们引入了”有序度“和”无序度“这两个概念来分析。

有序度是指数组中具有有序关系的元素的个数。

同理，对于一个倒序排列的数组，比如6,5,4,3,2,1，有序度为0。对于一个完全有序的数组，比如1,2,3,4,5,6来说，它的有序度是n(n-1)/2，我们把这种完全有序的数组的有序度叫作满有序度。

逆序度的定义正好跟有序度相反（默认从小到大为有序），我想你应该想到了。关于这三个概念有一个公式：逆序度 = 满有序度 - 有序度。

冒泡排序包含两个操作原子，比较和交换。每交换一次，有序度就加1。不管算法如何改进，交换的次数是固定的，就是逆序度。对于包含n个数据的数组进行冒泡排序，我们知道，当这个数组已经有序的时候，不需要进行交换，逆序度为0，最坏情况的时候，逆序度为n(n-1)/2，那么我们取一个平均就得到n(n-1)/4，那么它的平均时间复杂度就是O(n^2)。

2.空间复杂度

从代码中我们可以看到，这个算法只涉及一个替代的int类型，因此是一个原地排序算法

3.稳定性

从代码中我们可以看到，当数据相同的时候，没有发生交换，因此是一个稳定的排序算法。

插入排序

思路：首先，我们将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序的区间中的元素，在已排序的区间中找到合适的插入位置将其插入，并保证已经排序区间数据一直有序，直到未排序区间中元素为空，算法结束。注意这里在已排序的区间进行查找的话，我们要在最后开始进行查找。编程起来比较容易实现。

假设我们要排序的数据为：4,5,6,1,3,2，其中左边为已经排序的区间，右边是未排序的区间。

插入排序也包含两个操作，一个是比较，一个是移动。我们在插入一个数据的时候，需要将该位置后面的元素向后移动一位。不同的查找插入点方法，元素的比较次数可能不同，但是移动的次数总是固定的，就等于逆序度。其实跟冒泡一样，交换和移动的本质是一样的。

这里给出代码的实现：

void insert_sort(int* arr,int size){
    if(size <= 1){
        return;
    }
    for(int i=1;i<size;++i){
        int value = arr[i];  // 记录未排序区间的值,因为后面移位置已经改变。
        int j = i-1;        // 从最后开始寻找
        for(;j>=0;--j){
            if(value < arr[j]){
                arr[j+1] = arr[j];
            }else{
                break;
            }
        }
        arr[j+1] = value;// 这里加1的原因是--j已经后退了。
    }
}

分析：

1.空间复杂度：从代码中我们可以看到，这个算法是在原本数据上进行操作的，没有额外的空间消耗，所以这是一个原地排序算法。

2.稳定性：从代码中我们可以看到，当数据相同的时候，位置没有发生改变，因此是一个稳定的算法。

3.时间复杂度：当数组有序的时候，每次只需要比较一个数据就可以确定插入的位置，因此这种情况下，最好时间复杂度是O(n)。当数组倒序的时候，每一个数据都要遍历已经排序的区间，因此，最坏时间复杂度是O(n^2)。那么平均时间复杂度呢？同冒泡一样，我们借助有序度和逆序度的分析知道，平均时间复杂度还是O(n^2)。

选择排序

思路：跟插入排序一样，我们把整个数组也分成已排序区间和未排序区间，每一次都在未排序区间找到最小的值，然后放到已排序区间的末尾。

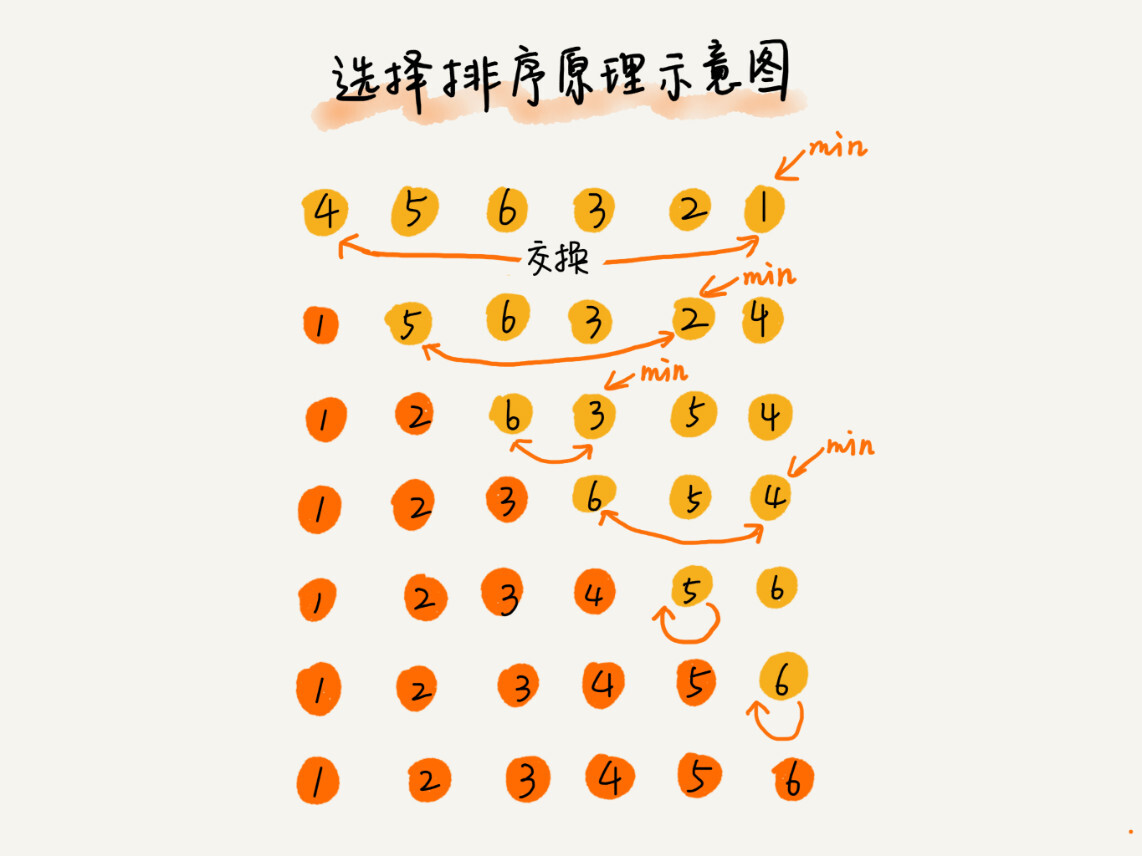
这里给出代码实现：

void selete_sort(int* arr,int capacity){
    if(capacity <=1){
        return;
    }
    for(int i=0;i<capacity;++i){
        int min_index = i; // 这里的min_index注意放在外面
        for(int j=i;j<capacity;++j){
            if(arr[j] > arr[min_index]){
                min_index = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[min_index];
        arr[min_index] = temp;
    }
}

分析：

1.时间复杂度

这里的选择排序没有最好的情况，也没有最坏的情况，从代码中，我们可以看出，对整个数组来说，要遍历数组中的每一个数，然后每一次数都要与已排序区间进行比较。因此最好时间，最坏时间，平均时间复杂度都是O(n^2)。

2.空间复杂度

整个算法是在原数组进行操作的，因此空间复杂度是O(1)，它是原地算法

3.稳定性

由于选择排序每一次都要找剩余未排序的元素的最小值，并和前面的元素交换位置，这样就破坏了稳定性。因此相对插入，冒泡来说，选择排序就不那么常用了。

归并排序

思路：如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

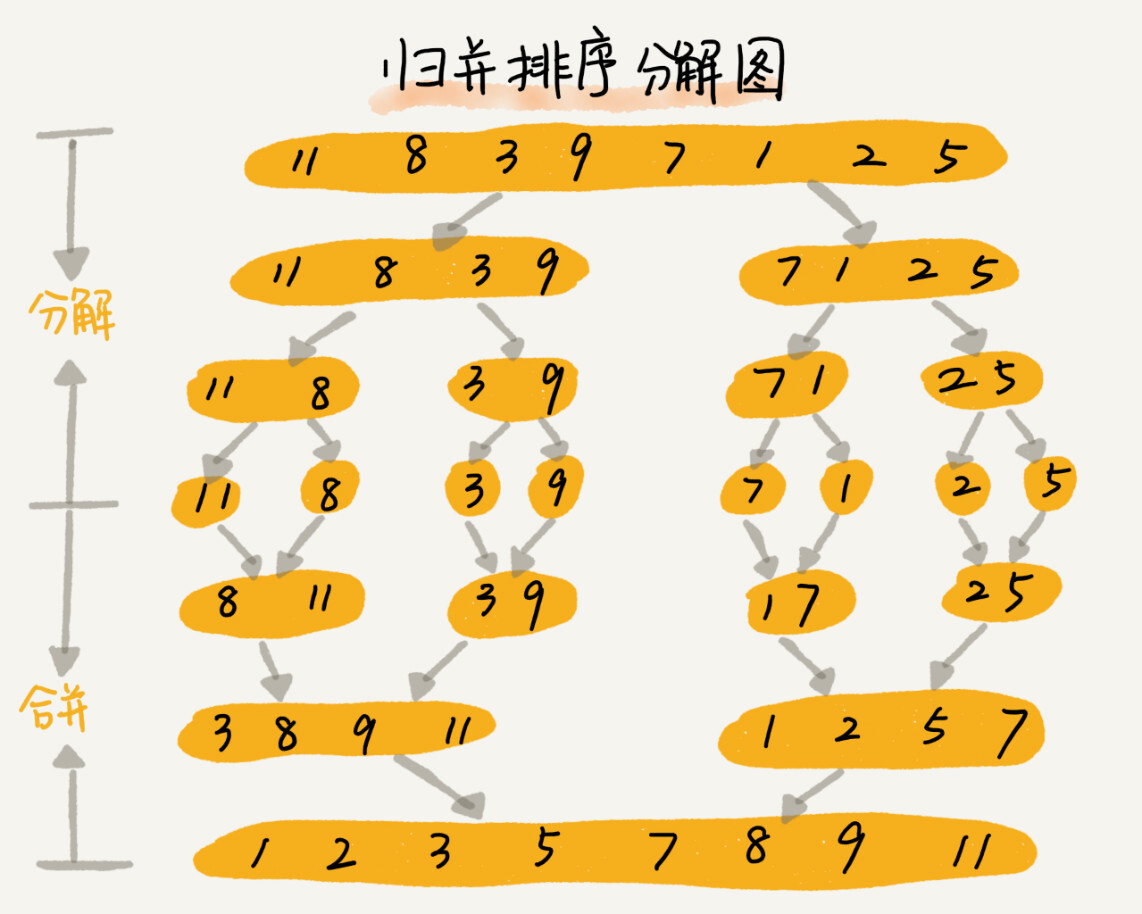
归并排序使用的是分治思想。分治，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。这样的分治思想很适合使用递归的编程技巧来实现。

我们先写出递推公式：

递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))

终止条件：
p >= r 不用再继续分解

所以现在问题的关键就转为如何实现merge函数，将两个已经排好序的部分拼接起来。其实这个问题我们在数组那里就做过了，它的本质其实就是两个有序的数组合并成一个有序的数组。

这里给出归并排序的代码实现：

void merge(int* arrays,int start,int end){
    int* temp = new int[end-start+1];
    int mid = start + ((end-start)>>1);// 防止两个数相加溢出
    int i=start,j=mid+1,k=0;
    while(i<=mid && j<=end){
        if(arrays[i] < arrays[j]){
            temp[k++] = arrays[i++];
        }else{
            temp[k++] = arrays[j++];
        }
    }
    if(i<=mid){
        for(;i<=mid;++i){
            temp[k++] = arrays[i];
        }
    }else{
        for(;j<=end;++j){
            temp[k++] = arrays[j];
        }
    }

    for(int count=0;count<(end-start+1);++count){
        arrays[start+count] = temp[count];
    }

}

void merge_sort_c(int* arrays,int start,int end){
    if(start >= end){
        return;
    }
    int mid = start + ((end-start)>>1);// 防止两个数相加溢出
    merge_sort_c(arrays,start,mid);
    merge_sort_c(arrays,mid+1,end);
    merge(arrays,start,end);
}

void merge_sort(int* arrays,int size){
    merge_sort_c(arrays,0,size-1);
}

int main(){
    int nums[6] = {6,2,4,3,5,1};
    merge_sort(nums,6);
    for(int i=0;i<6;++i){
        cout << nums[i] << endl;
    }

}

分析：

1.空间复杂度：

我们从merge函数中看出，每次merge函数都要开辟end-start+1的空间，但每一次函数都会释放，因此空间复杂度是O(n)。

2.稳定性：

我们在合并的时候，可以保持原来的顺序，因此它是一个稳定的算法。

3.时间复杂度：

递归代码的时间复杂度应该如何分析呢？

递归的适用场景是：一个问题可以分解成多个子问题b、c，那求解问题a就可以分解为求解问题b、c，问题b、c解决之后，我们再把b、c的结果合并成a的结果。如果我们定义求解问题a的时间是T(a)，求解问题b、c的时间分别是T(b)、T(c)，那我们就可以得到这样的递推关系：

T(a) = T(b) + T(c) + K

其中K等于将两个子问题b、c的结果合并成问题a的结果所消耗的时间。

我们假设对n个元素进行归并排序的时间是T(n)，那分解成子数组的时间是T(n/2)，合并的时间是O(n)，那么就有：

T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1

进一步分解有：

T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n
     ......

当T(n/2^k) = T(1)时，也就是n/2^k = 1，我们就可以得到k = log2n，带入上式，得到T(n) = n + nlog2n。如果我们使用大O表示法的话，那么他的时间复杂度就是O(nlogn)。另外，归并排序的执行效率与原始数组的有序度无关，所以其时间复杂度非常稳定，都是O(nlogn)。

快速排序

思路：如果要排序的数组中下表从p到r之间的一组数据，我们选择p到r之间的任意一个数据作为pivot（分区点）。我们遍历p到r之间的数据，将小于pivot的放到左边，大于pivot的放到右边，将pivot放在中间。经过这一个步骤，数组p到r之间的数据就分成了三个部分，前面p到q-1之间都是小于pivot的，中间是pivot，后面的p+1到r之间的是大于pivot的。

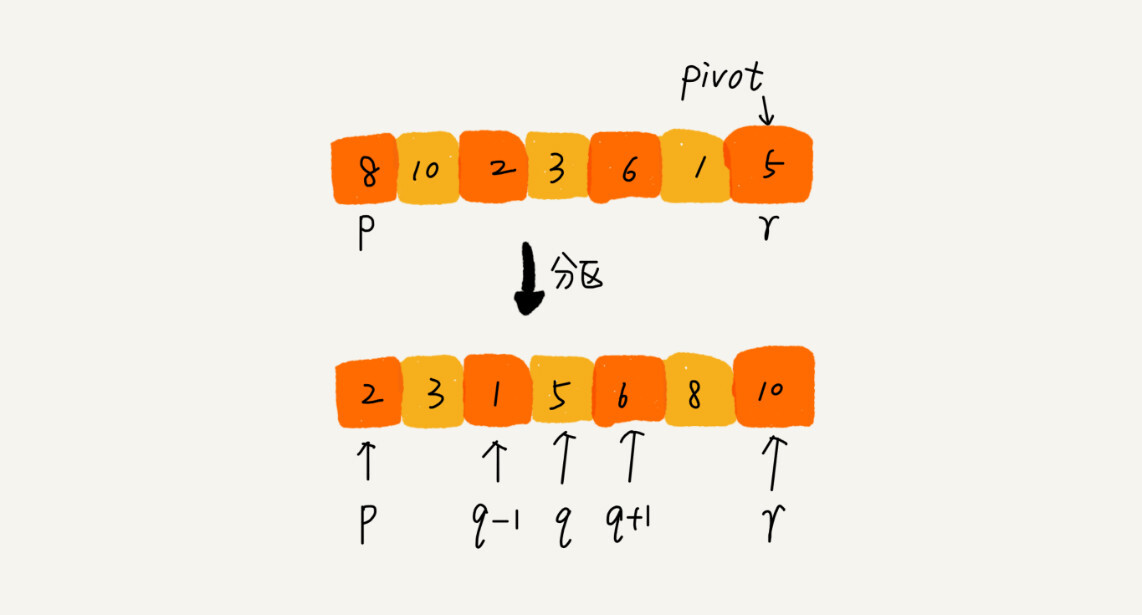
根据分治，递归的思想，我们可以用递归排序下标从p到q-1之间和下标q+1到r之间的数据，直到区间缩小为1，就说明所有的数据都有序了。

递归公式是这样的：

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)

终止条件：
p >= r

现在的问题就变成了如何实现分区函数，实现把小于pivot的放左边，大于pivot的放右边。思路是这样的：我们借鉴选择排序的算法，每一次都选择最后一个数作为pivot，然后通过一个游标i 把p 到 r-1 之间的数分为左区间和右区间，游标 j 遍历p 到 r -1之间的数据，每一次取一个数跟piovt 比较，如果小于piovt的话，就把它放到左区间的末尾，然后i向前一步，否则i不移动，直到j遍历到最后一个数据，然后将pivot与 i 指向的数据进行交换就完成了分区。

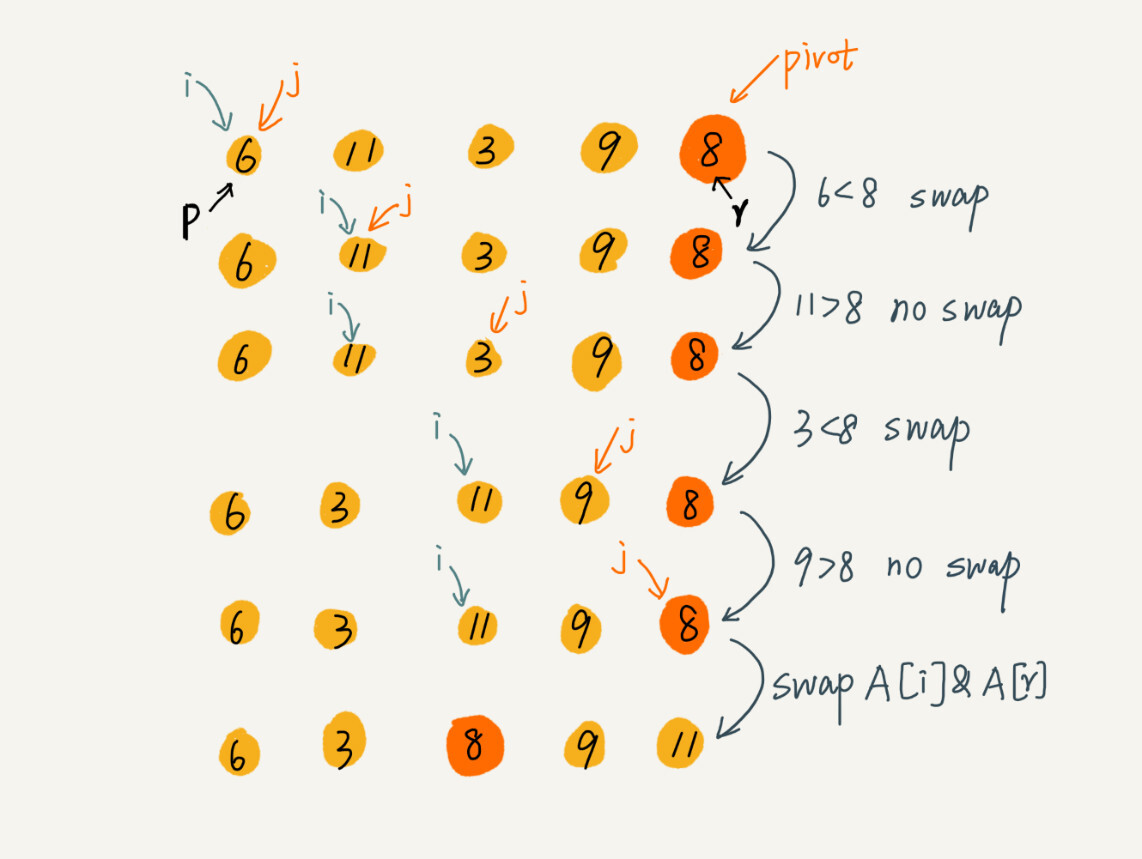
代码实现如下：

void merge_sort(int* arrays,int size){
    merge_sort_c(arrays,0,size-1);
}

int partion(int* arr,int start,int end){
    int pivot = arr[end];
    int i = start;
    for(int j=start;j<=end-1;++j){
        if(arr[j] > pivot){
            int temp = arr[j];
            arr[j] = arr[i];
            arr[i] = temp;
            ++i;
        }
    }
    arr[end] = arr[i];
    arr[i] = pivot;
    return i;
}

void quick_sort_c(int* arr,int start,int end){
    if(start >= end){
        return;
    }
    int p = partion(arr,start,end);
    quick_sort_c(arr,start,p-1);
    quick_sort_c(arr,p+1,end);
}

void quick_sort(int* arr,int size){
    quick_sort_c(arr,0,size-1);
}

int main(){
    int nums[6] = {4,5,3,1,2,6};
    quick_sort(nums,6);
    for(int i=0;i<6;++i){
        cout << nums[i] << endl;
    }
}

分析：

1.空间复杂度：从代码中可以看到，它是在原来数组上进行的操作，因此它是原地算法。

2.稳定性 ：因为有数据的交换，因此它是不稳定的算法。

3.时间复杂度：我们假设每一次分区函数都能够将p分到中间，那么最好时间复杂度就是O(nlogn)，另外如果每一次p都在最后，那么快速排序就退化为O(n^2)了。平均呢？由于结算起来非常复杂，这里直接给出结论：快速排序在大部分情况下的时间复杂度都为O(nlogn)，只有极少数为O(n^2)。

桶排序

思路：核心的思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

1.找出待排序数组中的最大值max、最小值min
2.我们使用动态数组vector作为桶，桶里放的元素也用 vector 存储。桶的数量为(max-min)/arr.length+1
3.遍历数组 arr，计算每个元素 arr[i] 放的桶
4.每个桶各自使用归并排序
5.遍历桶数组，把排序好的元素放进输出数组

这里给出代码的实现：

void bucket_sort(int* arr,int capacity){
    // find the min_value and the max_value
    int min_value = arr[0],max_value = arr[0];
    for(int i=0;i<capacity;++i){
        if(arr[i] < min_value){
            min_value = arr[i];
        }
        if(arr[i] > max_value){
            max_value = arr[i];
        }
    }
    // get the buckets number
    int buckets_num = (max_value - min_value) / capacity + 1;
    vector<vector<int>> buckets(buckets_num);
    // put the data into bucket
    for(int i=0;i<capacity;++i){
        int number = (arr[i] - min_value) / capacity;
        buckets[number].push_back(arr[i]);
    }
    // merge_sort in the buckets
    for(int i=0;i<buckets_num;++i){
        merge_sort(&buckets[i][0],buckets[i].size());
    }
    // show the result
    for(int i =0;i<buckets_num;++i){
        for(size_t j=0;j<buckets[i].size();++j){
            cout << buckets[i][j] << endl;
        }
    }
}

分析：

1.时间复杂度：

如果要排序的数据有n个，我们把它们均匀划分到m个桶内，每一个桶就有 k = n/m个元素。每个桶内部使用归并或者快速排序，时间复杂度就为O(klogk)。m个桶排序的时间复杂度就为O(m*klogk)，因为k = n /m，所以整个桶排序的时间复杂度就是O(n*log(n/m))。当桶的个数m接近数据个数n时，log(n/m）就是一个非常小的常量，整个时候桶排序的时间复杂度接近O(n)。从上面的代码分析可知，我们排序之前至少要遍历数据两遍，然后最后输出到一个数组的时候，也要遍历一遍，所以n前面有一个系数，但一般可忽略。

2.空间复杂度

首先桶的存在就需要占用内存了，因此它的空间复杂度是O(n)，另外如果我们采用归并排序，还要额外消耗空间。

3.稳定性

桶排序的稳定性取决于桶内部使用的排序算法，如果使用快速排序，它就是一个不稳定的算法，如果使用归并排序，那它就是一个稳定的算法。

适用场景：

这样看来桶排序十分优秀，那么能否取代我们之前的算法？

当然是否定的，首先，要排序的数据需要很容易划分成m个桶，而且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排完序之后，桶与桶之间的数据不需要再进行排序。

我们还要保证，数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不均匀，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为O(nlogn)的排序算法了。

桶排序比较适合用在外部排序中。所谓外部排序就是数据储存在外部磁盘中，数据量很大，内存有限，无法将数据全部加载到内存中。

比如你有10GB的订单数据，我们希望按订单金额进行排序，但是我们的内存有限，只有几百mb，这个时候就适合用桶排序了。我们先扫描一遍文件，找到最小，最大值。然后假设根据金额划分到100个桶里，我们依次取一个桶进行快速排序（不选归并是因为占空间）然后把排序后的结果写到磁盘，重复直到桶没有了。

计数排序

其实，计数排序可以看做是桶排序的特例。当要排序的数据n所处的范围不大，比如最大值是k，那么我们直接把数据划分成k个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。（与桶排序不同，桶排序的值的所处范围可以大于n，但是要易于划分）。

举个例子，比如高考的成绩查询系统，假设你所在的省有50万考生，考试分数的范围为0-900，这个数据的范围很小，所以我们可以分成901个桶。桶内的数据都是分数相同的学生，所以不再需要排序。我们值需要遍历即可，找到范围，然后再遍历一遍，把数据放在桶内，然后依次将桶内的考试输出到一个数组内，就完成了。时间复杂度是O(n)。

那么应该如何实现呢？我们通过一个实际的例子来。假设现在只有8个学生，分数在0到5之间。这8个选手的成绩我们放在数组score[8]里面，它们分别为：2,5,3,0,2,3,0,3。

我们遍历一次，得到score数组所处的范围为0到5，我们创建6个桶，使用一个buckets[6] 数组来表示。其下标对于分数，但储存的是考生的个数。我们只要遍历一遍考生分数，就能得到buckets数组。

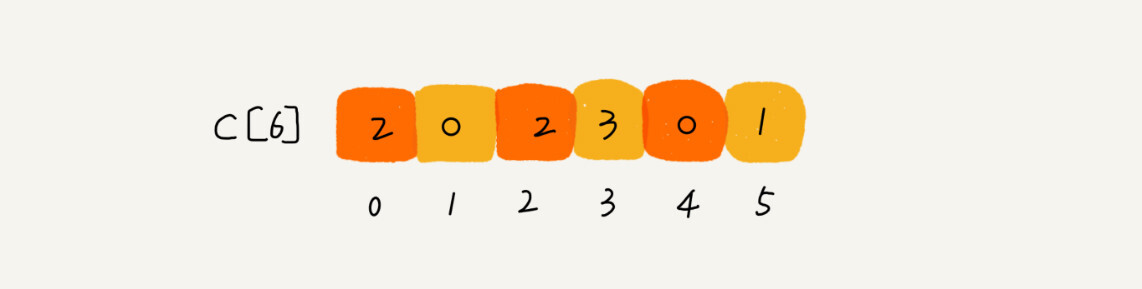
从图中，我们可以看出，分数为3的分考生有3个，，小于3分的有4个。我们创建一个有序的数组sort_score[8]，所以成绩为3分的考生在排序之后的有序数组R[8]中，会保存下标4,5,6的位置。

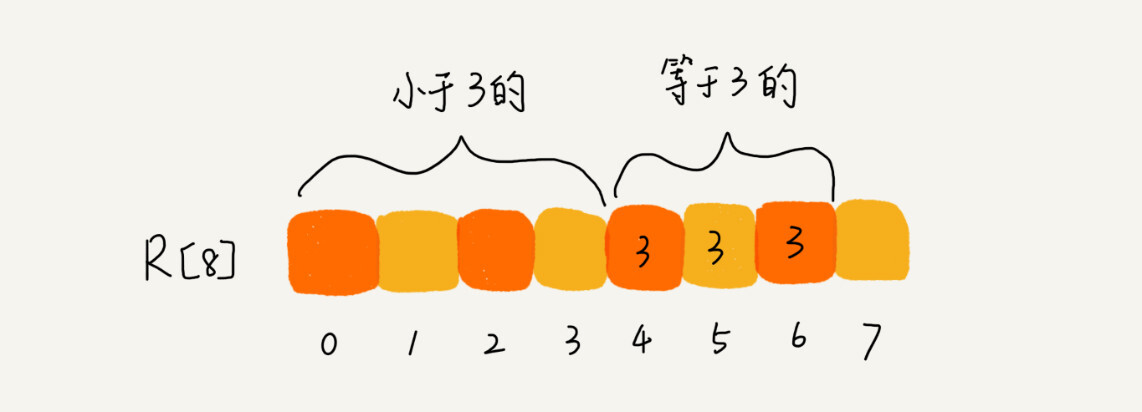
我们如何快速计算出，每个分数的考生在有序数组中对应的存储位置呢？这个处理的方法很巧妙，很不容易想到。

思路是这样的，我们对buckets[6]数组顺序求和，buckets[6]储存的数据就变成下面这样子。buckets[k] 里储存小于等于分数k的考生个数。

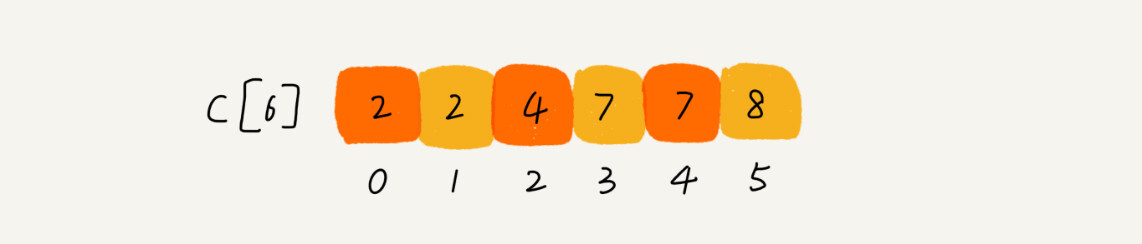
我们从后往前（为了稳定性）扫描原始数组score。比如扫描到3时，我们可以从数组score中取出下标为3的值7，也就是说，到目前为止，包括自己在内，分数小于等于3的考生有7个，也就是说3是数组sort_score中的第七个元素（下标为6）。当3放入到数组sort_score的时候，小于等于3的元素就只有6个了，所以buckets[3] 要减1，变成6。可以根据下面的图弄清楚。

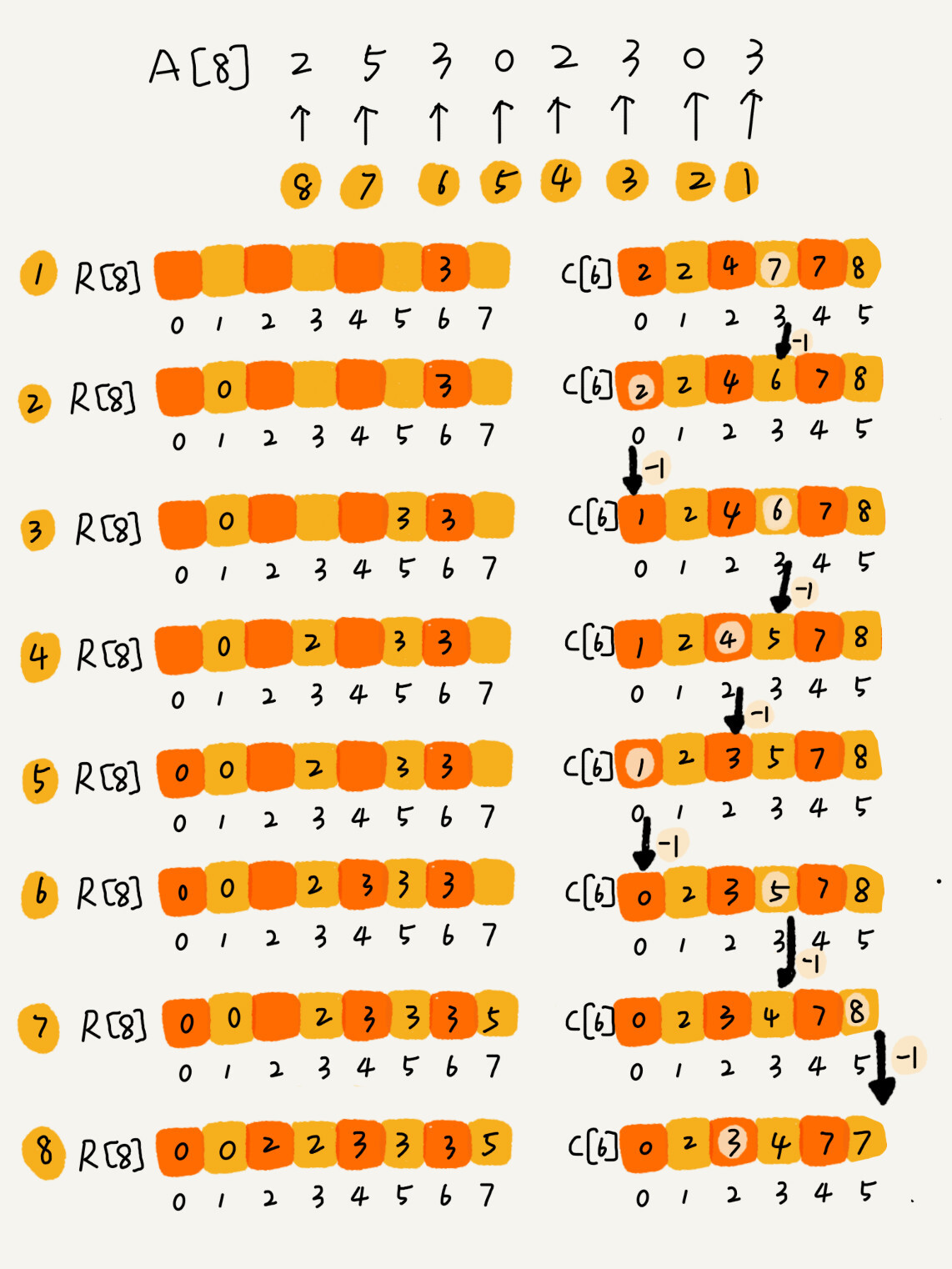
这里给出代码实现：

void countingSort(int* arrays,int capacity){
    if(capacity <= 1) return;
    // 查找数组中数据的范围
    int max = arrays[0];
    for(int i=1;i<capacity;++i){
        if(arrays[i] > max){
            max = arrays[i];
        }
    }

    // 计数数组赋值
    int count_array[max+1] = {0};
    for(int i =0;i<capacity;++i){
        count_array[arrays[i]]++;
    }

    // 依次累加
    for(int i=1;i<max+1;++i){
        count_array[i] = count_array[i] + count_array[i-1];
    }

    // 申请一个排序之后的数组
    int* temp = new int[capacity];
    for(int i = capacity-1;i>=0;--i){
        int row_value = arrays[i]; // 得到未排序的数据
        int index = count_array[row_value] - 1;// 得到计数数组的位置-1，得到索引
        temp[index] = arrays[i];// 将值赋给temp数组
        count_array[row_value]--;// 计数减1
    }

    // 将结果拷贝回去
    for(int i=0;i<capacity;++i){
        arrays[i] = temp[i];
    }
}

分析：

1.时间复杂度：

整个算法的过程只需要有限次的遍历，因此算法复杂度是O(n)。

2.空间复杂度：

由于我们需要一个temp的数组来储存排序后的数据，因此空间复杂度为O(n)。

3.稳定性：

我们从后往前开始遍历数组，可以保证算法是稳定的。

适用场景：

计数排序只能用在数据范围不大的场景中，如果数据范围k要比排序的数据n大很多，就不适合计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转换为非负整数。

基数排序

假设现在有这样一个问题，我们有10万个手机号码，希望将这10万个手机号码从小到达排序。有什么快速的排序方法？

如果我们使用之前的快速排序，时间复杂度可以做到O(nlogn)，手机号码有11位，范围太大，显然不适合用这两种排序算法。那么有没有时间复杂度是O(n)的算法呢？

刚刚这个问题有这样的规律，假设比较两个手机a,b的大小，如果在前面几位中，a手机号码已经b手机号码大了，那后面的几位就不用看了。

借助稳定的排序算法，这里有一个巧妙的实现思路，先按照最后一位来排序手机号码，然后，再按照倒数第二位重新排序，以此类推，最好按照第一位重新排序。经过11次排序之后，手机号码就有序了。注意，每一位的排序都要保证稳定，否则就没有意义了。还有，要排序的数据不一定都是等长的，比如我们排序牛津字典中的20万个英文单词，最短的只有1个字母，最长的有45，对于这种不等长的数据，我们可以把所有的单词补齐到相同的长度，位数不够可以在后面加0。因为根据ASCII值，所有字母大于0。

总结一下，基数排序对要排序的数据是有要求的，需要可以分割而出独立的“位”来比较，而且位之间有递进的关系，如果a数据的高位比b的数据大，那剩下的低位就不用比较了。除此之外，每一位的数据范围不能太大，要可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到O(n)。