SVM支持向量机 Support vector machine
像逻辑回归,解决的是二分类问题
(先讲解线性的 , 后面是非线性的)
SVM想要找的是能把两类数据分的最开的“胖边界”——也就是最好的决策边界

如上图,哪个边界才是最好的呢
同时我们把两类数据分成1 和-1 ,在边界上面的(红色点)视为1 ,下面的点(黄色点)视为-1
(逻辑回归是视为1和0,但是我们可以这样认为,我们的决策边界需要两者都要考虑,因此一个是1 另一个是-1)
那么我们把数据看成地雷,也就是要找出一条最安全的路
那么这条路当然是离雷越远越好

比起左边,我们更想要右边的边界对吧
那么从图上我们可以看到,影响这个边界的会是离我们最近的雷,也就是支持向量
支持向量机,也就是支持向量和决策边界
而在支持向量(离我们最近的雷)后面的雷(数量、分布)是不会对我们的决策边界有影响的
所以现在我们需要得到的是雷对我们边界的距离

假设现在的决策边界就是这个hyper plane ,有两个点符合在决策边界上的就符合1式
那么就可以用二式来表达法向量和平面垂直,
之后就可以有三式,用(x-x')表示求解点向量,和法向量的单位向量的内积就是将前者向量投影到法向量上的长度
而同时
如果等比放大缩小w b 看起来决策边界并没有变化,但是决策间隔却是改变了
例如,2w ,2b,决策边界没有改变但是间隔却是之前的两倍
就需要我们/ w的长度

那么这个也就是我们想要求的点到决策边界的距离
而对于有绝对值的直接求解是比较麻烦的,因此我们需要利用前面说到的将数据分为1和-1这个性质

可以看到 label和实际值(数值) 的乘积 一定出大于0 的,因此用这个等价代替了绝对值
(因为label只是1和-1,数值上没有改变实际值)

那么回想下,我们要找的决策边界是什么样的

是这样的 “胖边界” 对吧
因此就有了我们的优化目标

通常我们解决的手段是求偏导吧,但是这个可以直接各自对w b 求偏导然后解出来吗
并不好求吧(w,b 里外都有) 那么我们就可以考虑经常用的拉格朗日乘子法了,找出一个约束条件,构造出目标函数进行求解
下面就来找一个约束条件


那么此时就得到我们想要求的目标函数了

而我们经常求解的问题是求极小值、求梯度下降吧,因此将目标转换一下

那么就有


同时ai>=0
那么接下来讲解之后的求解思路:我们求的w,b 将先通过求偏导将式子转换为只关于ai的,然后用ai去求解最后结果,再利用w,b和a的关系将能求出w,b
而通过拉格朗日对偶性

可以先求w,b的偏导

接着,需要先讲述一个问题:如果不满足约束条件怎么办(因为我们的约束条件是更严格了的,也就有可能原来满足的但是现在不满足了)
不满足约束条件我们可以令ai=无穷大,那么可以知道我们求的目标也会是=无穷大的值,并不满足我们的需求,因此需要对a求max(这部分仅是个人理解)当所有约束条件都满足时,才会有对w,b的最优解
实际上
求对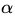
我们可以理解在没有w,b式子中求出符合条件的逼近最优解的问题中需要对a求max
(此时的式子可理解成是一个梯度上升的问题)

之前说到求w,b是需要a作为中介来求解,这里就需要用到对偶问题,用原问题的对偶问题
(还不如说是建立在原问题上的对偶问题)来求解a
而下面是july大神的理解

将上面的两条式子代回到原来的式子中,得到

接下来就是针对a的求解

同样的, 这里常用的方式是将求极大值转换为求极小值(理解成凸函数)
之后的求解就不是直接求偏导,而是用SMO算法
SMO算法需要选择合适的两个变量做迭代,其余的变量做常量来进行优化
在这里直接用一个例子来讲解怎么做最后的计算


这里 x * x 是点进行内积 例如 i=1 j=1时 ,(3,3) * (3*3)=9+9=18
那a1a2的42是怎么来的呢——i=1 j=2 和 i=2 j=1 两种情况相加,(3,3)*(4,3)=12+9=21 ——21*2 =42
之后就是对a1和a2求偏导

在这里可以理解为a1和a2这个函数是一个类似x^2的函数,那么极小值点不在范围内的话就有可能在 我们范围的边界上
我们知道最后的ai后就可以由w,b和ai关系代回得到w, b的值

这个就是例子中的hyper plane 也就是我们边界
那么这时候我们可以知道对我们的决策边界起作用的支持向量 其a不等于0
后面没什么用的数据点会是 a =0

因此后面一部分的点, 只要支持向量不变的话,决策边界不会变
上面的数据点是分布比较有规律的,有些数据就有可能成为噪声点

像上面的那个点,它偏离了正常的点的分布,但是它也是一个支持向量,对决策边界产生影响
这就是软间隔问题
针对这个问题,我们可不可以让它一定程度上忽略这种点,允许点一定程度上偏离决策边界
这个就是松弛因子

因此就有了需要考虑松弛因子的目标函数

我们引入C这个需要我们自己制定的参数来对松弛因子进行控制
我们要求极小值时,C很大,那么松弛因子会很小,也就意味着分类严格,不能允许有点偏离
C很小,那么松弛因子会很大,那么就允许点偏离边界的程度也就大
之后同样也是用拉格朗日乘子法进行类似的求解

约束中的条件是由对w,b,和松弛因子进行求偏导得到,就有了新的约束,之后再代回
得到类似的式子,借助ai得到最后的解
以上就是线性的SVM的求解
下面是对非线性
即以非线性的边界来划分数据,这是针对低维不可分的问题
利用核变换,将数据映射到高维上,然后在高维上将数据分开

这也是为什么上面的式子中不直接是x 而是关于x的表达式

而我们利用核函数,不需要在高维上计算数据,直接在低维上处理即可,降低了计算复杂性
也就是在低维空间上完成高维度样本内积的计算
其中一个经常使用的就是高斯核函数

很明显,对于非线性可以顺利划分的数据,用高斯核函数可以顺利划分
对于高斯核函数,我们在编程中是使用gamma来控制器复杂程度,gamma值越大,其复杂程度越大,投影的维度越高,就越容易发生过拟合

好像说左边的都能分得开,但是很明显的,容易出现过拟合现象,
虽然右边的分类情况可能不那么好,但是相对的,泛化能力也越强
参考博客:july大神的SVM