xaero最近创新出了新的学习方式,那就是拿着稿子上台去水一把吧,互相教学的高效方法。然而,我好像趁xaero不在水过了这简短的40分钟。(雾)
所以决定再整理一下讲稿,重新登在博客上。
第一章 矩阵乘法
作为一个学OI的同学,在座的一定都听说过矩阵,也知道矩阵怎么运算(或许还有人不知道?雾)。但我们还是来总结一下。
初识矩阵
首先矩阵是一个n*m的“矩阵”,n行m列的每一个元素都是数字。
大致就是这样: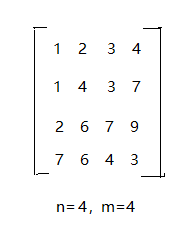
运算法则
加减法就是对应到矩阵的每一个元素的加减,并且这也并不常用到。
关键在于乘法。显然乘法是要求相乘的两个矩阵的大小必须满足nr和rm。换言之,第一个矩阵的列和第二个矩阵的行必须相等。但这其实也没什么重要,因为正常情况下,矩阵乘法往往是方阵乘法(方阵即n=m的矩阵)。
矩阵的乘法法则大致是确定一号矩阵的行i,再确定二号矩阵的列j,然后将行列的元素按顺序相乘再相加然后放在新矩阵(i,j)的位置上。
直观理解一下矩阵A*矩阵B:
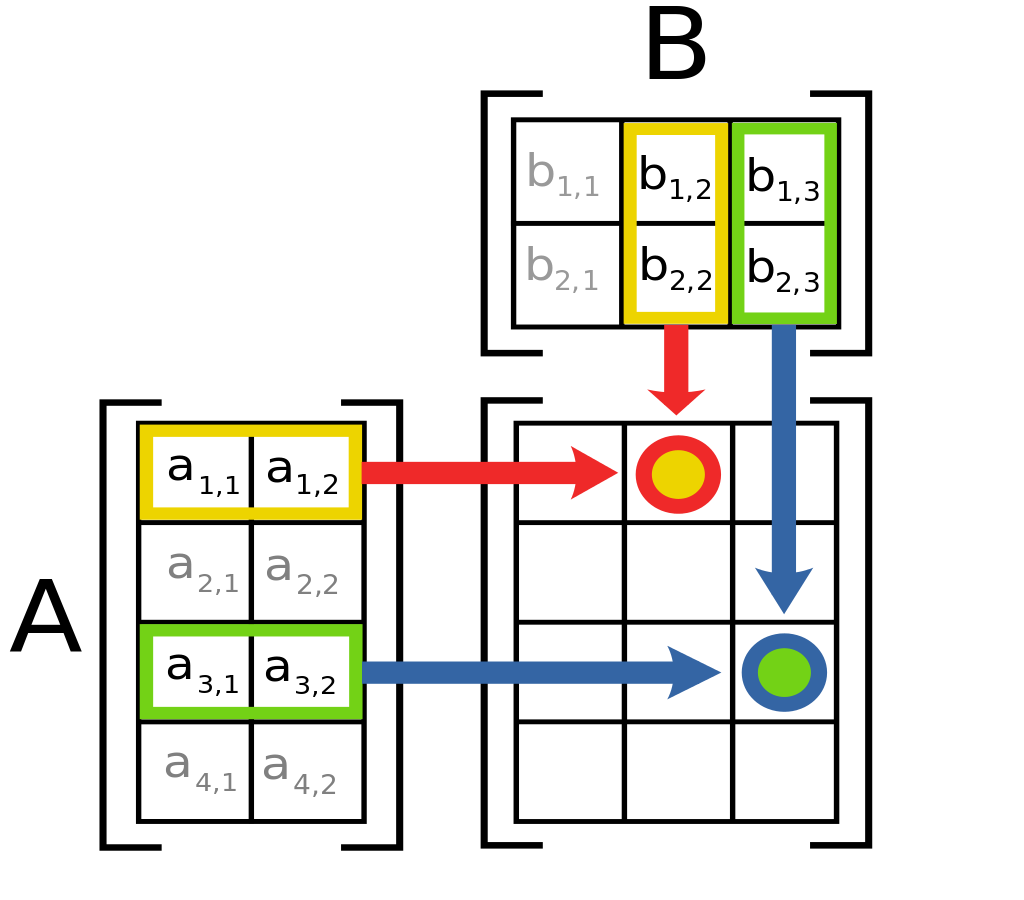
**矩阵满足结合律,不满足交换律,多个矩阵相乘时是从右向左运算,就像函数一样(事实上矩阵乘法的本质就是变换,而所有的变换都是从右向左运算的)。
**矩阵的乘法,本质上是一种变换,但是满足乘法和交换律的性质所以可以用快速幂来加快变换的速度。
经典例题
来看几道题。
求fibonacci数列第n项。O(n)递推?没问题,n<=10e12次方(mod 998244353)。这时候我们需要从矩阵的角度入手,先构造出一步变换的矩阵。通过F(i)和F(i-1)得到F(i+1)和F(i):
=
关于推出Fn,直接成左乘方程n次即可。由于矩阵乘法满足结合律,所以可以先对左边矩阵求n次幂。
用矩阵快速幂即可快速推出。
时间复杂度为O(n3log2T),n为方阵边长,T为项数。
求fibonacci前n项和。同理,再用Sn表示前n项和,把Sn考虑进转移矩阵即可快速算出。
各地省选
[HNOI2008]GT考试(矩阵优化dp决策)
先从dp方程入手。定义f[i][j]表示到第i位匹配到j位相同的方案数。问题在于转移,并不是每一次失配都要j回到0重新匹配,而是有可能像kmp一样失配时候回到之前的某个位置。这里我们定义辅助数组G[i][j]表示从第i位转移到第j位是否存在。这样定义显然不是最优的,但这样我们可以进行矩阵优化。因为有
可以看成矩阵乘法(注意F[n]和G都为矩阵):
显然可以矩阵快速幂优化。答案即是
。
[code]
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=2e5+1000;
int n,m,mod;
int g[30][30];
char s[30];
void kmp(){
int nxt[30],j=0;
nxt[0]=0,nxt[1]=0;
for(int i=2;i<=m;i++){
while(j>0&&s[i]!=s[j+1])j=nxt[j];
if(s[j+1]==s[i])nxt[i]=++j;
else nxt[i]=0;
}
for(int i=0;i<m;i++){
for(int j='0';j<='9';j++){
int k=i;
while(s[k+1]!=j&&k>0) k=nxt[k];
if(s[k+1]==j) k++;
if(k<m)g[i][k]++;
}
}
}
inline void mul(int a[30][30],int b[30][30]){
int c[30][30];
for(int i=0;i<m;i++){
for(int j=0;j<m;j++){
c[i][j]=0;
for(int k=0;k<m;k++)
c[i][j]=(c[i][j]+a[i][k]*b[k][j])%mod;
}
}
for(int i=0;i<m;i++)
for(int j=0;j<m;j++)
a[i][j]=c[i][j];
}
int pw(int p){
int r[30][30];
for(int i=0;i<m;i++)
for(int j=0;j<m;j++)
r[i][j]=i==j?1:0;
while(p>0){
if(p&1)mul(r,g);
mul(g,g),p=p>>1;
}
int ans=0;
for(int i=0;i<m;i++) ans=(ans+r[0][i])%mod;
return ans;
}
int main(){
cin>>n>>m>>mod;
scanf("%s",s+1);
kmp();
cout<<pw(n)<<endl;
return 0;
}
小结:关于dp的矩阵优化,我觉得最重要的一点就是看出dp决策是固定的(即不基于状态)。然后根据之前谈到的一个重要思想,那就是把决策(或者说是状态的转移)看成一种固定的变换,抽象成一个矩阵。然后用快速幂来加速这种变换。
**还有一点就是关于F[n],必定是可以滚动存储的。如果不可以滚动则一定不可以。
[SCOI2009]迷路(矩阵证明、拆点)
首先定义一个邻接矩阵。先假设所有边的长度均为1,则这个矩阵自乘T次之后(i,j)的值,就是i到j长度为T的路径的方案数。证明如下:
先定义初始矩阵D1(D)任意元素
为i到j是否存在边(或者看作是i到j长度为1的路径的方案数)。Dn中的元素表示从i到j的路径长度为n的方案数。则显然有
。即
。然后矩阵快速幂即可。
问题在于边长不为1。但其实边长也挺小的。所以就把n个点拆成9n个点。假装点9i有一个走j秒后的点9*i+j。然后就可以愉快的快速幂了。
[code]
#include<bits/stdc++.h>
using namespace std;
const int N=128;
const int mo=2009;
int n,T;
struct mat{
int a[N][N];
void clr(){
memset(a,0,sizeof(a));
}
}a;
mat operator *(mat a,mat b){
mat re;
re.clr();
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
re.a[i][j]=(re.a[i][j]+a.a[i][k]*b.a[k][j]%mo)%mo;
}
}
}
return re;
}
mat operator ^(mat a,int b){
mat re;re.clr();
for(int i=1;i<=n;i++)re.a[i][i]=1;
while(b){
if(b&1)re=re*a;
a=a*a;
b>>=1;
}
return re;
}
int main(){
scanf("%d%d",&n,&T);
int n1=n;
n=n*9;
for(int i=1;i<=n1;i++){
for(int j=1;j<=8;j++){
a.a[9*(i-1)+j][9*(i-1)+j+1]=1;
}
}
char s[32];
for(int i=1;i<=n1;i++){
scanf("%s",s+1);
for(int j=1;j<=n1;j++){
if(s[j]>'0'){
a.a[9*(i-1)+s[j]-'0'][9*(j-1)+1]=1;
}
}
}
a=a^T;
printf("%d",a.a[1][n1*9-8]);
return 0;
}
小结:还是强调关注变当中的不变。固定的一套转移过程可以抽象成矩阵的乘法,但看出来并不容易,还是需要勤加练习锻炼感觉。
第二章 高斯消元
高斯消元是一种时间复杂度为O(n^3)的消元算法。主要用途是求解线性方程组,当然也可以求解矩阵的秩和矩阵的逆。
主要步骤分为两步,消元和回代。
和某写dalao的写法不同,我是在确定一个元之后同时进行消元和(伪)回代。
模板非常的裸,称之为模拟也不为过。看一下代码就可以理解了。(这个矩阵为“增广矩阵”第n+1列表示y的值)

**注意高斯消元时的精度问题。还有这里判断return0时,其实省略了一些分类讨论。
分类讨论1、 如果发现确定某一元出现了等于0的情况。那么它可能是跑到了其他的某一行中,形如
的形式,两个元之间纠缠不清,使得它们两个可以等于无数个值。或者说是整个线性方程组与它无关。总的来说那一元变成了可以等于任意数的自由元。但其他某些数还是可以得到精确值的。
分类讨论2如果发现某一行的系数全为0,但第n+1列不为0。则相当于用消元证明整个方程组存在矛盾。方程无解。
**这里的题目不太会有这样的讨论。但在“第三章 线性空间”中,求矩阵的秩时就会遇到分类讨论1。
经典例题
luogu P2962 灯(高斯消元)
高斯消元从不拘泥于一般形式的方程组求解问题。换成异或和也依然可以。但注意异或和时,会出现自由元。利用dfs定位一个方案即可。
当然这道题由于点较少的原因,所以可以用双向bfs水过。
[code]
#include<iostream>
#include<cstdio>
#include<climits>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int read(){
int q=0;char ch=' ';
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')q=q*10+ch-'0',ch=getchar();
return q;
}
int n,m,ans=INT_MAX;
int a[40][40],x[40];
void gauss(){//高斯消元
int i,j,bj,k;
for(k=1;k<=n;k++){
bj=k;
for(i=k+1;i<=n;i++)if(a[i][k]){bj=i;break;}
if(bj!=k)for(j=1;j<=n+1;j++)swap(a[bj][j],a[k][j]);
for(i=k+1;i<=n;i++)if(a[i][k]){
for(j=1;j<=n+1;j++)a[i][j]^=a[k][j];
}
}
}
void dfs(int xx,int tot){
if(tot>ans)return;//剪枝
if(!xx){ans=min(ans,tot);return;}
if(a[xx][xx]){//如果消元后系数为1,则用高斯消元的判断方法进行判断
x[xx]=a[xx][n+1];
for(int j=n;j>xx;j--)x[xx]^=x[j]&a[xx][j];
if(x[xx])dfs(xx-1,tot+1);
else dfs(xx-1,tot);
}
else {//如果为0就随便定一个
x[xx]=0;dfs(xx-1,tot);
x[xx]=1;dfs(xx-1,tot+1);
}
}
int main()
{
int i,j,xx,yy;
n=read();m=read();
for(i=1;i<=m;i++){xx=read();yy=read();a[xx][yy]=a[yy][xx]=1;}
for(i=1;i<=n;i++)a[i][n+1]=1,a[i][i]=1;
gauss();dfs(n,0);printf("%d",ans);
return 0;
}
小结:高斯消元其实是一种应用面很广的算法。性质上犹如dp或是lca一样,是非常好用的解题工具。可以通过消元理清一些一些关系。例如某些有后效性的dp方程,也可以通过消元化简来取得实际意义。
第三章 线性空间。


各地省选
[JLOI2015]装备购买
一道典型的知识点题目。知道就是会做,不知道就是不会做。
显然要求就是求极大生成子集且子集中的向量线性无关。
装备数量即是秩的数量。
而花费最少,只要贪心即可,消元时每次取前k-1列为0k列不为0且花费最小的行进行消元即可。(还是反证法证明构造其余矩阵均不最优)。
[code]
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=510;
const long double eps=1e-8;
int n,m,c[maxn],cnt,ans;
long double g[maxn][maxn];
void gauss(){
for(int i=1;i<=m;i++){
int bj=0;
for(int j=cnt+1;j<=n;j++)
if(fabs(g[j][i])>eps&&(!bj||c[bj]>c[j]))
bj=j;
if(bj==0) continue;
cnt++,ans+=c[bj];
for(int j=1;j<=m;j++)
swap(g[cnt][j],g[bj][j]);
swap(c[cnt],c[bj]);
for(int j=i+1;j<=m;j++)
g[cnt][j]/=g[cnt][i];
for(int j=1;j<=n;j++){
if(j!=cnt&&fabs(g[j][i])>eps){
for(int k=i+1;k<=m;k++)
g[j][k]-=g[cnt][k]*g[j][i];
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
double temp;scanf("%lf",&temp);
g[i][j]=temp;
}
for(int i=1;i<=n;i++)
scanf("%d",&c[i]);
gauss();
printf("%d %d\n",cnt,ans);
return 0;
}