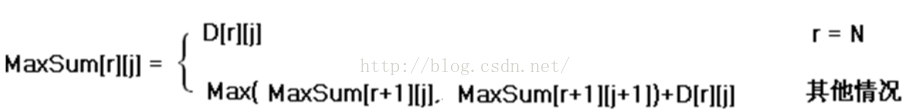关于动态规划,是很重要的一部分内容,说实话,现在我脑子里还转不过来这个弯,但我发现其实比较多的DP问题都可以用递归来做,但是就是超时,所以要再加数组来记忆,叫记忆化搜索(我看有些地方也叫记忆化递归)。还是要做题才能加深理解啊。。。。
关于递归,我也不是很清楚他的运行,但是有位大佬总结的比较好,拿来主义
递归函数的执行流程分为两个阶段:递归前进段、递归返回段。
这可以说一个很神奇的东西。总的来说就是:递归前进段就是你按它函数的顺序执行下去,直到碰到边界;递归返回段就是当你碰到了边界,你把刚刚所有递归嵌套的函数值算出来,一步一步返回值,返回给最初的值。
这里有一个我很容易搞错的东西,也很难理解的东西:没每递归调用一次函数,系统就会生成一个新的函数实例。这些函数实例有同名的参数和局部变量,但各自独立,互不干扰。流程执行到哪一层,那一层的变量就起作用,返回上一层,就释放掉低层的同名变量。这个需要深刻理解一下。
递归到动规的一般转化方法
1 递归函数有n个参数,就定义一个n维的数组
2 数组的下标是递归函数参数的取值范围
3 数组元素的值是递归函数的返回值,这样就可以从边界值开始, 逐步填充数组,相当于计算递归函数值的逆过程。
动规解题的一般思路(我感觉确定状态比较难)
1. 将原问题分解为子问题
- 把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。子问题都解决,原问题即解决(数字三角形例)。
- 子问题的解一旦求出就会被保存,所以每个子问题只需求 解一次。
2.确定状态
- 在用动态规划解题时,我们往往将和子问题相关的各个变量的一组取值,称之为一个“状 态”。一个“状态”对应于一个或多个子问题, 所谓某个“状态”下的“值”,就是这个“状 态”所对应的子问题的解。
- 所有“状态”的集合,构成问题的“状态空间”。“状态空间”的大小,与用动态规划解决问题的时间复杂度直接相关。 在数字三角形的例子里,一共有N×(N+1)/2个数字,所以这个问题的状态空间里一共就有N×(N+1)/2个状态。
整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。在数字三角形里每个“状态”只需要经过一次,且在每个状态上作计算所花的时间都是和N无关的常数。
3.确定一些初始状态(边界状态)的值
以“数字三角形”为例,初始状态就是底边数字,值就是底边数字值。
4. 确定状态转移方程
定义出什么是“状态”,以及在该“状态”下的“值”后,就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”(递推型)。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方程”。
数字三角形的状态转移方程:
能用动规解决的问题的特点
1) 问题具有最优子结构性质。如果问题的最优解所包含的 子问题的解也是最优的,我们就称该问题具有最优子结 构性质。
2) 无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。