解题报告 smoj 2019初二创新班(2019.3.31)

T1：单人游戏
T2：赚金币
T3：抽奖

时间：2019.4.5

比赛网址

T1：单人游戏

题目描述

棋盘由N个格子排成一行，从左到右编号为1到N，每个格子都有一个相关的价值。
最初，棋子位于第1个格子上，当前方向是向右的。

在每个回合中，棋子在当前方向上行走零步或多步，每一步就是走一个格子。然后在下一回合中，棋子的方向反转。

一开始，玩家总得分是0分。

每次棋子从格子A移动到格子B，那么从A至B这一段连续的格子的得分都会累加到玩家的总得分去。

如果某次移动会使得玩家总得分小于0，那么玩家肯定不会进行这样的移动。

如果允许玩家最多进行k次移动，输出玩家获得的最高总得分。

分析

---前方大量证明预警---

大眼观察样例，我们发现：玩家跳跃多次后，总会在一个区间上反复跳跃。我们称这个区间为“环”。

举个例子：如图，区间\([8, 10]\)（红色部分）就是“环”

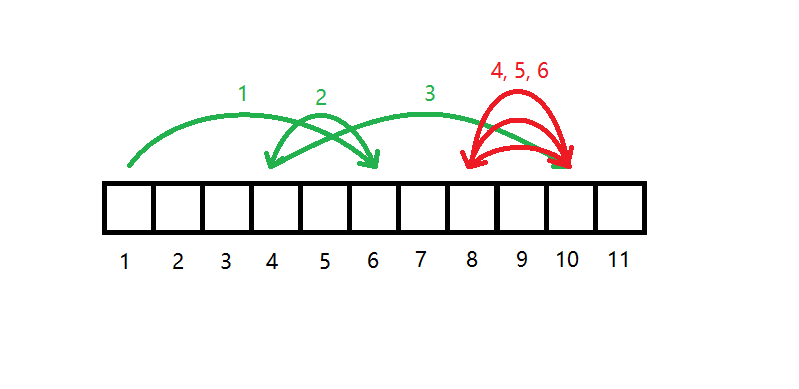
但是，对于所有情况游戏都有环吗？下面我们来证明这一点。

证明：游戏必定存在环

假如我们将每次跳跃后的得分贡献（就是题中的部分和）组成一个序列\(Q\)，考虑\(Q\)的最后一项\(Q_k\)

首先，\(Q_k\)必定是整个序列中最大的。不然前面肯定存在一个最大值\(Q_i\)，这样我们就可以在\(i\)这一步上反复跳跃，让序列\(\ge i\)的位置都变成\(Q_i\)，比原序列答案要优。

其次，与\(Q_k\)相同的数必定占据\(Q\)中最后连续的位置。不然前面也会存在一个\(Q_i = Q_k\)，且\(i\)不在最后连续的位置，我们可以在\(i\)这一步上反复跳跃，让序列\(\ge i\)的位置都变成\(Q_i\)，仍比原序列答案要优。

综上所述，序列\(Q\)中必定存在一个最大值，且这个最大值占据了\(Q\)最后连续的位置。这个最大值（和这些最大的位置）就是“环”。

在证明的过程中，我们发现环的得分贡献是最大的。因此可以发现以最少的跳跃到达环是最佳选择。

证明：以最短路径到达环必定最优

假设不以最短路径到达环，那么在到达环的路径上肯定会在某个地方多转几下。
又因为环的得分贡献最大，故这在别的地方多转的几下肯定不如跑到环上去转。
故以最短路径到达环必定最优（当然，在保证路径最短的情况下，要挑得分高的路径跳）。

另外，我们还发现一个性质：每一次移动都会在环前面的格子进行

即：若环是区间\([l, r]\)，那么我们不会走到\(> r\)的位置去。这能为我们的程序提供一定的便利（例如无后效性）

证明：移动时不可能越过环的结尾

如图，假设环是区间\([l, r]\)，\(j\)是环后\(> r\)的一个位置。我们要从\(i\)跳到\(l\)上，并顺便在环上“蹭”一下，有两种选择：

直接从\(i\)跳到\(r\)，再从\(r\)跳到\(l\)；
从\(i\)跳到\(j\)，再从\(j\)跳到\(l\)。

这两种方案对得分的贡献分别是\(sum (i, r) + sum (l, r)\)和\(sum (i, j) + sum (l, j) = sum (i, r) + sum (l, r) + sum(r + 1, j) \times 2\)。

由上面证明环的得分贡献最大这条性质知\(sum (r + 1, j) \le 0\)，不然当前的环还可以向右“扩张”，不会对最终答案（即题目输出）造成影响。

故第二种方案不可能比第一种方案优，移动时越过环的结尾只会吃力不讨好。

由上面这些证明可以得出一个贪心策略：若已知环的位置，求出到达环的最短路径，并在满足路径最短时得分最大。又有移动时不可能越过环的结尾，此题的解决已经很明显了。

DP实现

设\(suf(i)\)为以\(i\)结尾的最大部分和。一边计算前缀和时一边维护\(min1\)，表示\(\le i\)中前缀和的最小值。\(suf(i) = sum(i) - min1\)

设\(f(i)\)为从起点开始跳到\(i\)的最少步数。设\(g(i)\)为在满足\(f(i)\)最小时当前得分的最大值。

若我们要从\(j\)跳到\(i\)，检查一下\(g(j) + sum(j + 1, i)\)是否大于等于0。若为正数，直接更新答案即可。若为负数，说明无法一步从\(j\)跳到\(i\)，需要在\(suf(j)\)上跳若干（偶数）次。用\(\left \lceil \dfrac {-(g(j) + sum(j + 1, i))} {suf(j) \times 2} \right \rceil \times 2\)求出需要跳跃的次数，并更新答案。

更新答案时，若目前\(f\)与\(f(i)\)相同，取\(g(i)\)大的答案。

环可能不是原棋盘中的最大部分和。因此我们需要枚举环。若环结尾是\(i\)，根据贪心可以选择\(suf(i)\)这一段。结果就是\(g(i) + (k - f(i)) * suf(i)\)

---细节见代码---

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int kMaxN = 100 + 10;
const LL kInf = 9000000000000000000ll;
// 9e18
int T, n;
LL k, a[kMaxN];
LL min_sum;
LL sum[kMaxN], suf[kMaxN];
LL f[kMaxN], g[kMaxN];
LL ans;
inline LL GetSum(int l, int r) {
  return sum[r] - sum[l - 1];
}
inline LL DivCeil(LL a, LL b) {
  return (a + b - 1) / b;
}
void Debug() {
  printf("a:\n  ");
  for (int i = 1; i <= n; i++) printf("%lld ", a[i]);
  printf("\nsum:\n  ");
  for (int i = 1; i <= n; i++) printf("%lld ", sum[i]);
  printf("\nsuf:\n  ");
  for (int i = 1; i <= n; i++) printf("%lld ", suf[i]);
  printf("\nf:\n  ");
  for (int i = 1; i <= n; i++) printf("%lld ", f[i]);
  printf("\ng:\n  ");
  for (int i = 1; i <= n; i++) printf("%lld ", g[i]);
  printf("\n");
}
int main() {
  freopen("2843.in", "r", stdin);
  freopen("2843.out", "w", stdout);
  scanf("%d", &T);
  while (T--) {
    scanf("%d %lld", &n, &k);
    min_sum = 0;
    for (int i = 1; i <= n; i++) {
      scanf("%lld", &a[i]);
      sum[i] = sum[i - 1] + a[i];
      min_sum = min(min_sum, sum[i]);
      suf[i] = sum[i] - min_sum;
    }
    for (int i = 1; i <= n; i++) {
      if (sum[i] >= 0) {
        f[i] = 1; g[i] = sum[i];
      } else {
        f[i] = kInf; g[i] = 0;
      }
      for (int j = 1; j <= i - 1; j++) {
        LL score = g[j] + GetSum(j + 1, i); // 从j跳来后的得分
        if (score >= 0) { // 如果可以直接从j跳来
          if (f[j] < f[i]) { // 从j转移更优
            f[i] = f[j];
            g[i] = score;
          } else if (f[j] == f[i]) { // 尝试更新g数组
            g[i] = max(g[i], score);
          }
        } else if (suf[j]) {
          LL times = DivCeil(-score, suf[j] * 2) * 2;
          if (f[j] + times < f[i]) {
            f[i] = f[j] + times;
            g[i] = score + times * suf[j];
          } else if (f[j] + times == f[i]) {
            g[i] = max(g[i], score + times * suf[j]);
          }
        }
      }
    }
    // Debug();
    ans = 0;
    for (int i = 1; i <= n; i++) {
      if (f[i] <= k) {
        ans = max(ans, g[i] + (k - f[i]) * suf[i]);
      }
    }
    printf("%lld\n", ans);
  }
  return 0;
}

T2：赚金币

题目描述

在游戏中，你刚刚建立了\(a\)个工厂并聘请了\(b\)专家。不幸的是，你现在还没有留下金币，你想以最快的速度赚到\(target\)金币。游戏进行多轮，在一轮中，您获得\(a \times b\)单位的黄金，其中\(a\)是工厂数量，\(b\)是您目前拥有的专家数量。在每轮结束时，您可以建立更多工厂并雇用更多专家。建立一个新工厂或雇用一个新的专家成本是\(price\)金币。只要您能负担得起，您拥有的工厂和专家数量就没有限制。至少要多少轮游戏，才能完成目标？

数据范围：\(\Large 1 \le a, b, price, target \le 10^{12}\)

分析

观察发现数据范围都很大，且并没有单调性（游戏轮数并不能二分）

我们发现一个贪心策略：

每次购买一件物资（工厂或专家），只购买数量少的一方。

证明：显然，若\(a \le b\)，那么\((a + 1) \times b \ge a \times (b + 1)\)，而我们想让每局物资数量的乘积尽量高。

这个策略提示我们：完成目标时，物资中数量少的一方，数量最多为\(\bf{\sqrt n}\)

也就是说，物资购买的总数最多为\(2\sqrt n\)。这启示我们枚举购买的物资数。

这时，我们又发现：如果决定要购买\(k\)件物资，那么这些物资越快买完越好。这样我们就可以空出时间来积攒金币了。

若当前拥有\(a\)个工厂和\(b\)位专家，当前金币数量是\(money\)，我们可以通过\(\left \lceil \dfrac {\max(price - money, 0)} {a \times b} \right \rceil\)算出下一次购买需要的回合数。

同理可以通过\(\left \lceil \dfrac {\max(target - money, 0)} {a \times b} \right \rceil\)算出以当前的物资达到目标需要的回合数。

直接从\(1\)到\(2 \times 10^6\)枚举购买的物资数即可。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL kInf = 1e13;
const int kMaxBuy = 2000000 + 10;
int T;
LL a, b, price, target;
LL money, round_;
LL ans;
inline LL DivCeil(LL a, LL b) {
  return (a + b - 1) / b;
}
int main() {
  freopen("2844.in", "r", stdin);
  freopen("2844.out", "w", stdout);
  scanf("%d", &T);
  while (T--) {
    scanf("%lld %lld %lld %lld",
        &a, &b, &price, &target);
    if (a > b) swap(a, b);
    if (a > kMaxBuy) {
      printf("1\n");
    } else {
      ans = kInf;
      round_ = 0;
      money = 0;
      if (a * b >= target) {
        printf("1\n");
        continue;
      }
      for (int i = 0; i <= kMaxBuy; i++) {
        // 购买
        LL times = DivCeil(max(price - money, 0ll), a * b);
        round_ += times;
        money = money + a * b * times - price;
        a++;
        if (a > b) swap(a, b);
        // 更新答案
        if (money >= target) {
          ans = min(ans, round_);
          break;
        } else {
          ans = min(ans, round_ + DivCeil(target - money, a * b));
        }
      }
      printf("%lld\n", ans);
    }
  }
  return 0;
}

T3：抽奖

题目描述

黑箱子里面有N种不同类型的彩球，每次你只能从箱子摸一个彩球出来，第i种彩球出现的频率是p[i]（即概率为\(\dfrac {p[i]} {sum}\)）。问要摸多少次才能凑齐所有类型的彩球，输出期望值。

分析

移项期望裸题。

设\(F(S)\)表示已经摸到过了\(S\)集合中的彩球，凑齐所有类型的彩球期望需要的次数。

直接贴代码（滑稽）

（代码中为了方便传了一个cnt参数，表示\(S\)的大小）

代码

#include <bits/stdc++.h>
using namespace std;
const int kMaxN = 20 + 10;
const int kMaxSet = 1 << 22;
int T;
int n, times[kMaxN], tot;
double p[kMaxN];
double arr_f[kMaxSet];
double F(int S, int cnt) { // Have got balls in S, cnt = S.size()
  if (cnt == n) {
    return 0;
  } else if (arr_f[S] != -1) {
    return arr_f[S];
  } else {
    double prob = 0;
    double sum = 0;
    for (int i = 0; i < n; i++) {
      if (S & (1 << i)) {
        prob = prob + p[i]; // !!!
      } else {
        sum += p[i] * ( 1 + F(S | (1 << i), cnt + 1) );
      }
    }
    return arr_f[S] = (prob + sum) / (1 - prob);
  }
}
int main() {
  freopen("2846.in", "r", stdin);
  freopen("2846.out", "w", stdout);
  scanf("%d", &T);
  while (T--) {
    scanf("%d", &n);
    tot = 0; // !!!
    for (int i = 0; i < n; i++) {
      scanf("%d", &times[i]);
      tot += times[i];
    }
    for (int i = 0; i < n; i++) {
      p[i] = 1.0 * times[i] / tot;
    }
    for (int S = 0; S < (1 << n); S++) {
      arr_f[S] = -1;
    }
    printf("%lf\n", F(0, 0));
  }
  return 0;
}