离散余弦变换
由于实信号傅立叶变换的共轭对称性，导致DFT后在频域中有一半的数据冗余。离散余弦变换(DCT)在处理实信号时比离散傅立叶(DFT)变换更具优势。在处理声音信号这类实信号时，DFT得到的结果是复功率谱，其结果中的一半数据是没利用价值的。相比之下，DCT得到的结果是实谱，从而节省了不必要的运算。
一个序列的DFT就是将其周期拓展后取其DFS系数的一个周期。如果序列的开始及结尾处的幅值差异较大，那么这个周期拓展的序列便会有较多的高频分量。
而序列的DCT（实序列）相当于一个长度是它两倍的实偶序列的DFT（普通序列的DFT＝实序列＋虚序列），在储存同样个数的数据的情况下，DCT的能量更集中在低频。
DCT还有一个很重要的性质（能量集中特性）：大多书自然信号（声音、图像）的能量都集中在离散余弦变换后的低频部分，因而DCT在（声音、图像）数据压缩中得到了广泛的使用。由于DCT是从DFT推导出来的另一种变换，因此许多DFT的属性在DCT中仍然是保留下来的。（归一化之后，会在高频产生很多0系数，说明DCT比FFT变换具有更好的能量聚集度。）
DCT在图像处理中优于DFT的性质是更高的能量聚集度，根本原因是二维DCT和二维DFT变换空间的基底不同。二维DFT的变换空间基底（谐平面波分量）是由sin和cos平面波共同构成的。而二维DCT的变换空间基底（谐平面波分量）是由cos单独构成的。
图像经过二维DFT变换后，大部分能量集中在频谱空间的四个角落（低频分量）；而图像经过二维DCT变换后，大部分能量集中在频谱空间的左上角（低频分量）。此所谓DCT的能量集中度优于DFT者也。
推导
推导N点长实序列的DCT，首先来定义一个新的长度为2N的序列：
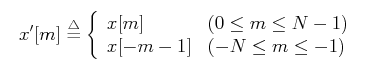
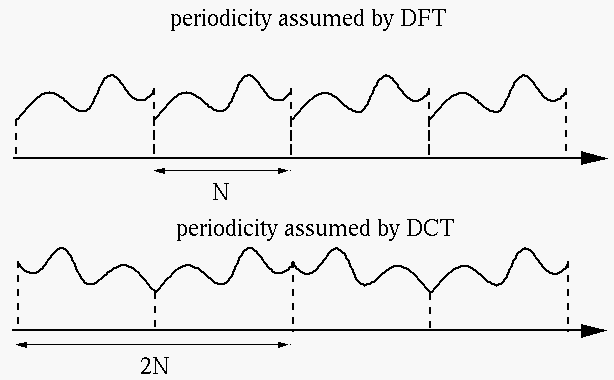
DCT可看作是将周期为N的序列x[m]做一个周期延拓成一个周期为2N的序列。如下图。
再来看第一张图是关于 x = -1/2 对称的，要让其关于x = 0对称需要将其向右平移1/2个单位，得到 x’[m] = x’[m – 1/2] 就是关于 x = 0对称的周期序列了（如第二张图）。
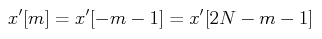
上述 2N 点的偶对称序列的 DFT计算过程为：
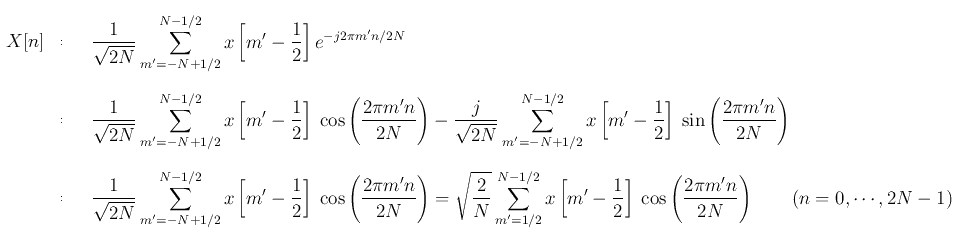
其中
是偶对称的，
分别是偶数和奇数。将
替换为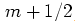
，可以得到DCT为：
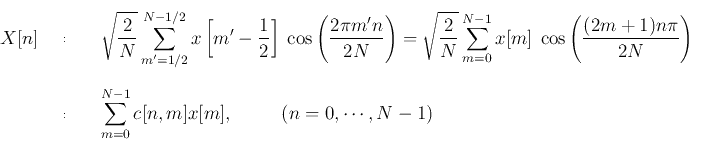
系数定义为c[n, m] ，则
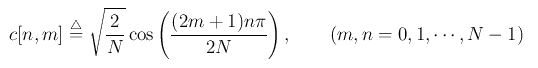
有DCT系数矩阵C∈RN×N，上述为C的第n行第m列的元素。又因为在n=2N的周期内，X[n]=X[-n]是偶对称的。进一步有：
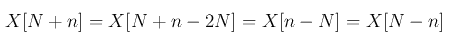
则n从N,...,2N-1的期间，X[n]是多余的，can be dropped。则n的范围变为0,...,N-1。除了第一个n=0，C的所有行向量都是正交归一化的：
为了使得DCT是正交变换，定义系数：
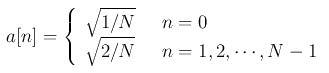
其中c[n, m]被a[n]修正。余弦变换矩阵为：
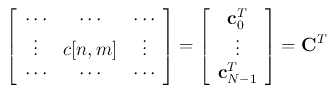其中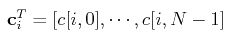 
是DCT变换矩阵C的第i行。
上述行向量都是正交的：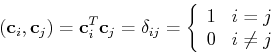
，则变换矩阵C也是正交的：
，且
。
则DCT变换可以表示为矩阵形式：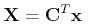
，两边左乘C得到：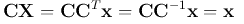
逆DCT有：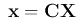
，也可以表示为：
总结
与 DFT 相比，DCT 有两个主要优点:
- 它是一种比 DFT 具有更好的计算效率的真实变换, 它的定义是一个复杂的变换。
- 它不引入间断, 同时在时间信号中施加周期性。在 DFT 中, 当时间信号被截断并假定为周期性时, 在时域中引入了不连续性, 并引入了相应的频率域中的工件。但是, 当截断时间信号时, 即使采用对称性, 也不会在 DCT 中引入间断和相关工件。
参考：http://fourier.eng.hmc.edu/e161/lectures/dct/node1.html
去相关性
在图像处理中，通常来说，正交变换具有去相关性。其中最理想的是KLT（Karhunen Lo`eve Transform ），DCT是KLT最大程度上的近似，在视频图像处理中被广泛应用。
从数学的角度上来看，去相关性就是把原取样点的自相关矩阵通过DCT变换，变成一个对角矩阵，而且对角线上的值是取样点自相关矩阵的特征值。这样一来，去相关后的矩阵保留了原矩阵的重要信息（特征值），而过滤到了一些不相关的量。这对后续的处理（比如量化、编码）都非常有意义，它使得矩阵变“瘦”，而关键信息不变，这样一来算是对原关键信息的一种增强，提高了后续的图像还原质量。
扩展
傅立叶变换的FT物理意义是将一个在时间域当中的信号所包含的所有频率分量（主要指其各频率分量的幅度和相位）用一个以角频率为自变量的函数表示出来，称其频谱。
但是并不是所有的信号都能取傅氏变换（例如当该信号不满足狄利特里条件时），所以在傅氏变换的积分函数中的积分因子上乘以一个exp(a)，使之满足可积条件，是为拉氏变换。
傅里叶变换是拉氏变换的特例，相当于S平面虚轴上的拉氏变换
一个信号的抽样取拉氏变换与相应的离散信号与Z变换的作用是等效的。Z变换与拉氏变换之间是一对多的映射关系，Z平面上的单位圆对应于S平面上的虚轴；Z平面上的单位圆内部分对应于S平面上的左半平面；此外，S平面是直角坐标平面，Z平面则是极坐标平面。
离散傅里叶变换相当于是Z变换在Z平面单位圆上的情况（即是Z变换的特例)
FFT
FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。
假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。 而第一个点就是直流分量，它的模值就是直流分量的N倍。而每个点的相位呢，就是在该频率下的信号的相位。第一个点表示直流分量（即0Hz），而最后一个点 N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被 N-1个点平均分成N等份，每个点的频率依次增加。
Fn所能分辨到频率为 Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。如果要提高频率分辨力，则必须增加采样点数，也即采样时间。频率分辨率和采样时间是倒数关系。
假设采样频率为Fs，采样点数为N，做FFT之后，某一点n（n从1开始）表示的频率为：Fn=(n-1)*Fs/N；该点的模值除以N/2就是对应该频率下的信号的幅度（对于直流信号是除以N）；该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值，范围从-pi到pi。要精确到xHz，则需要采样长度为1/x秒的信号，并做FFT。要提高频率分辨率，就需要增加采样点数，这在一些实际的应用中是不现实的，需要在较短的时间内完成分析。解决这个问题的方法有频率细分法，比较简单的方法是采样比较短时间的信号，然后在后面补充一定数量的0，使其长度达到需要的点数，再做FFT，这在一定程度上能够提高频率分辨力。