大家的人工智能——线性回归

在《大家的人工智能——学习路线总览》中，相信大家已经对人工智能领域已经有了一个初步的了解，现在我们从其中一个小方面入门机器学习，今天我们将要讲述的是机器学习中的一种线性模型——线性回归。

什么是线性回归

让我们把思绪先倒回到初中数学课堂上（如果你已经上过初中），来回顾一个知识点：一元一次方程，给出如下坐标点(1,1.5)，(2,2)，(3,2.5)，要求计算出当x=4时，y的值。

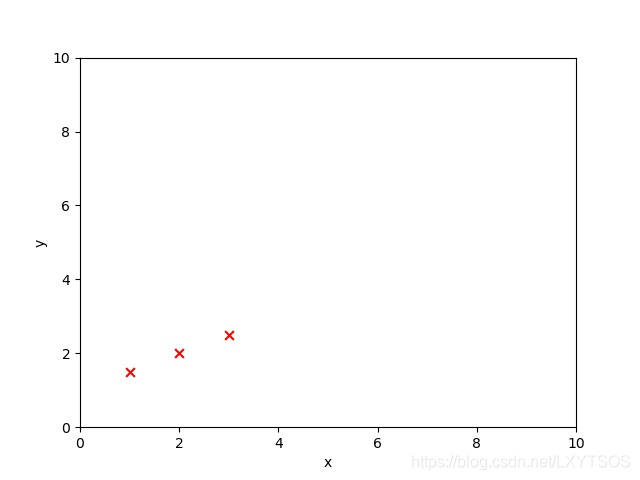
在这里插入图片描述

相信大家都会首先求出一条经过这三个点的直线y=1/2x+1，再将x=4代入求得y=3。使用给出的三个点坐标（训练数据），求出一条直线方程（模型），然后计算一个新的x对应的y值（回归，或预测）。大家早在上中学的时候就开始使用线性模型进行回归啦。

那么计算机如何使用这些数据（比如上面的三个点）得到一个拟合（可以理解成很好的将数据点连起来）这些数据的模型（比如上面的直线）呢？计算机可是不知道要首先假设曲线方程为y=ax+b喔，而且也不知道将两个点坐标代入假设出的直线方程然后联立求解出a和b喔。大家好不好奇计算机如何来得到拟合效果好的曲线呢。

假设

我们以一元线性回归（一个自变量）为例，我们假设最终需要找到一条直线:

$y = wx+b$

我们把之前的a替换成w，w在这里表示这个特征（x）所占的权重，即重要程度。那么现在只要我们找到w和b能够使这条直线很好的拟合给出的数据就大功告成啦。

如何寻找w和b

如果要求一条直线的方程，我们人首先会选取两个比较好的点代入方程中，联立求出w和b来，但是让计算机来解方程那就有一定难度啦，那么计算机是如何找出w和b的呢？

像前面所说，首先会给我们一堆已知x和y的点(x1,y1)，(x2,y2)，···，(xn,yn)。
然后随机初始化w和b的值，也就是随机初始化出一条直线。
选取一个点，将x代入这条直线中求出y’，然后计算出y’和真正的y相差多少。
通过算法调整w和b来减少y’和y之间的差值。
重复3-4这个步骤，就能慢慢逼近最佳的w和b啦。

代价函数

说到差值，大家最先想到的是讲两个数相减，越小就说明差别越小。但是如果计算许多y’和y差值的总和的话，每对y’和y的差值有正有负，加在一起会抵消掉一部分使得差值总和降低，因此不简单的使用两个值的差，而是在每个差值上平方一下，让它们都为正数，再把所有差值都加起来算平均，得到最终的差值，这就叫做均方误差（mean-square error, MSE），而计算误差的函数我们成为代价函数（Cost Function），或者损失函数（Loss Function）。现在我们已经知道如何来定义这些差值了，下面用数学公式来表示。

首先我们把直线方程改写一下便于区分：

$h_{\theta}(x) = \theta_0 + \theta_1x$

那么根据上面的均方误差计算方式，可以将代价函数写成下面的形式：

$J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)} - y^{(i)})^2$

其中i表示第几个样本点，m表示样本个数，求和前面分母中的2是为了求导之后形式更美观而加上的。

现在我们已经得到一个代价函数啦，我们再来看看上一节说到的，通过减少差值来调整w和b，因此，这里的目标就是如何最小化这个代价函数（最小二乘），而找到使得它最小的θ0和θ1就能得到我们最终想要的那条直线。

现在先回到高中课堂，当我们碰到要求一个函数的极值时，就对它求导，导数为0的地方就是极值。如何让计算机来找到这个最低点呢，我们来观察一下上面的代价函数，它是一个凸函数（想象成一个碗）。

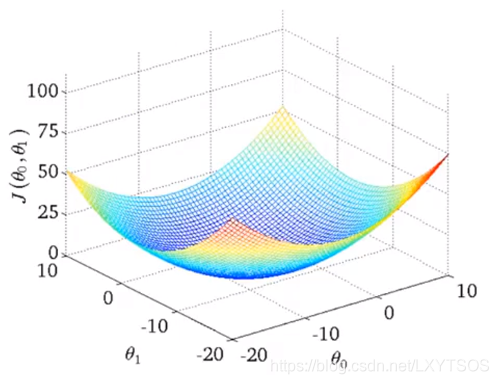
在这里插入图片描述

或者用等高线图来表示：

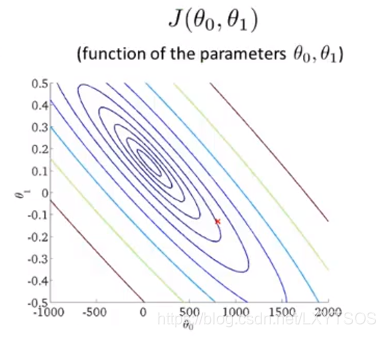
在这里插入图片描述

同一个圈上的损失值是一样的，越往里损失值越小。

记得我们在最开始随机挑选了θ0和θ1（w和b）的值吗？也就是在代价函数这个碗上的一个点，我们如何让这个点像下楼梯一样一点一点地往最低处走呢？

梯度下降

首先我们来看一张环境比较复杂代价函数图：

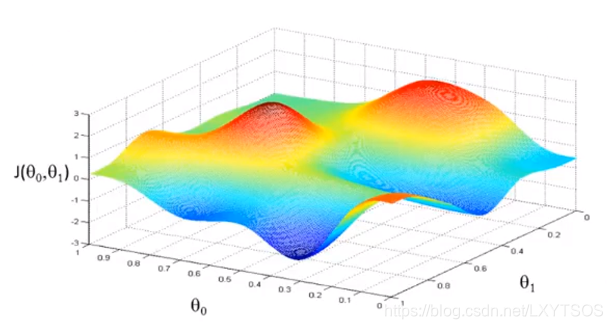
在这里插入图片描述

随机在这个图上选一个点，然后一步一步往当前觉得最低的地方走：

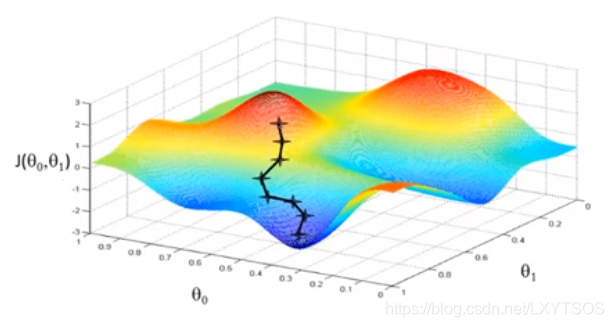
在这里插入图片描述

如果挑了另外一个点呢，那路线可能完全不同了，会走到其他低处去，比如起始点在之前的基础上往右一点：

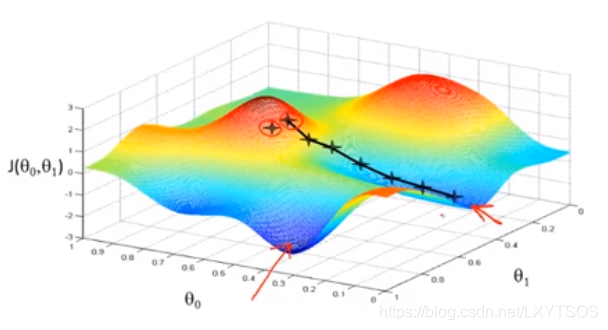
在这里插入图片描述

可以很明显看到，由于起始位置的不同，可能最后找到两个不同的局部最优解（局部最小值）。

那么是什么机制可以让这个点一步一步往最低处走呢，它可不会像球一样依靠万有引力往低处滚的喔。下面介绍梯度下降算法，就是这种算法能使这个点一步一步往低处走，这里先给出梯度下降算法更新θ（往下走）的形式，稍后再以图的形式展示：

$\theta_j = \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1)$

分别计算j=0与j=1时的值，其中α表示学习率，可以想象成一步跨多大的步伐，之后的部分就是对代价函数求偏导计算梯度了。

看到数学公式是不是觉得头晕？不用怕，下面用图像形式来展示梯度下降是如何工作的，为了方便展示，下面考虑单变量情形（只有一个θ），那么前面看到的碗状的曲面这个时候就是一个抛物线。

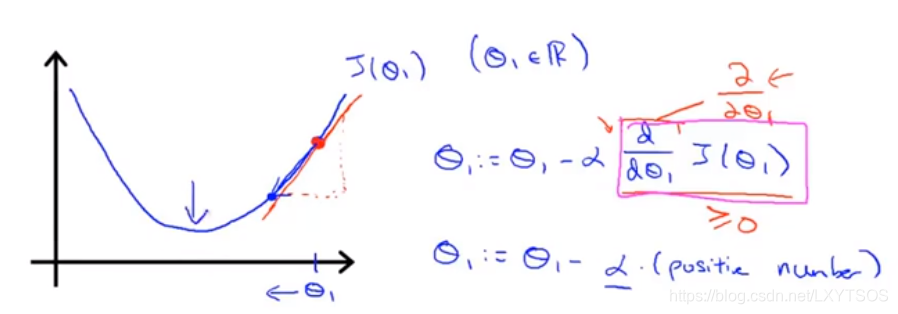
在这里插入图片描述

假如初始点落在了右边（红色那个点点），现在求代价函数在这个点处的梯度（导数），也就是那条红色切线的斜率，很明显是个正数，然后学习率乘以梯度得到需要下降多少，因此θ的值会慢慢往左边走。

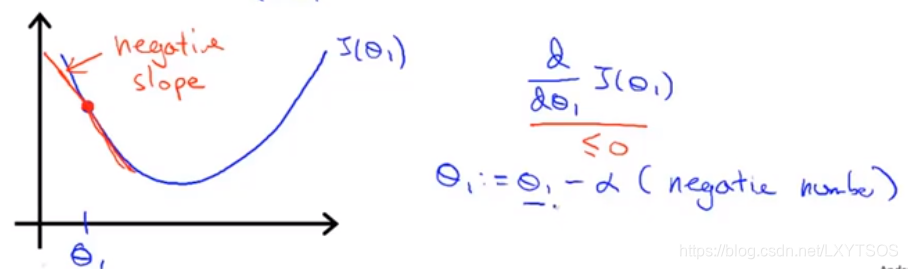
在这里插入图片描述

假如初始点落在了左边，那么这个点处的梯度是个负数，θ减去这个值实际上是在增大θ，因此θ会慢慢往右走落向最低处。

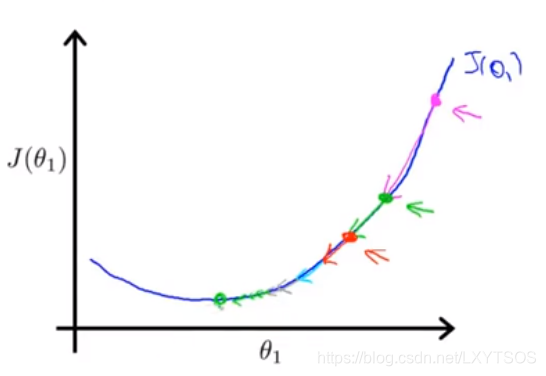
如果学习率α太小，就像一个人步子迈的小，就要走很多步才能到最低点：

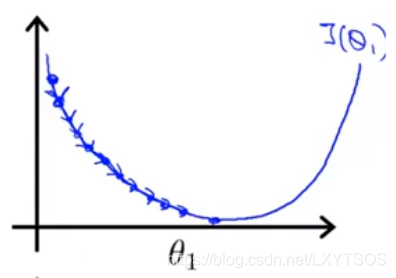
在这里插入图片描述

如果学习率α太大，可能会跨过最低点，甚至有时候会发散根本找不到最低点：

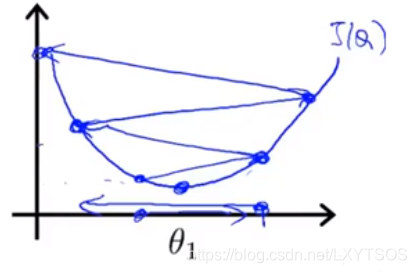
在这里插入图片描述

如果保持一个相对小的学习率不变，梯度下降也能收敛到局部最小，如下图：

在这里插入图片描述

我们可以看到，从最右边的点开始，每进行一次下降，所处位置的梯度值就更小，所以θ每次减的值越来越小，步伐也就越来越小，慢慢能够收敛到全局最小。

基于梯度下降衍生出了很多不同的算法，为了加快下降速度以及找到向较好的方向下降，这里就不详细讲解了。

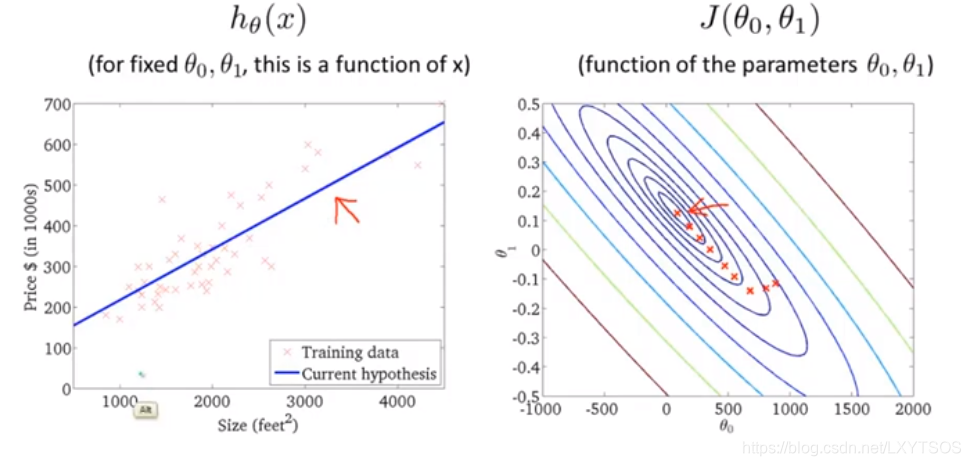
当找到最小化代价函数的θ的时候，也就找到了一条能最好拟合数据的直线：

在这里插入图片描述

实践一下

讲了那么多理论的东西，大家是不是觉得有点困倦了，现在我们用sklearn框架来实践一下，使用sklearn中自带的数据集，选其中一维来演示。

我们把训练数据显示在图上：

在这里插入图片描述

现在我们要使用这些点拟合出一条直线出来，然后在测试数据上看看效果，在sklearn中只要调用linear_model中的LinearRegression就能够很便捷地训练出一条直线出来：

from sklearn import datasets, linear_model
regr = linear_model.LinearRegression()
regr.fit(diabetes_X_train, diabetes_y_train)

训练出一条直线之后，我们在测试数据上看看效果：

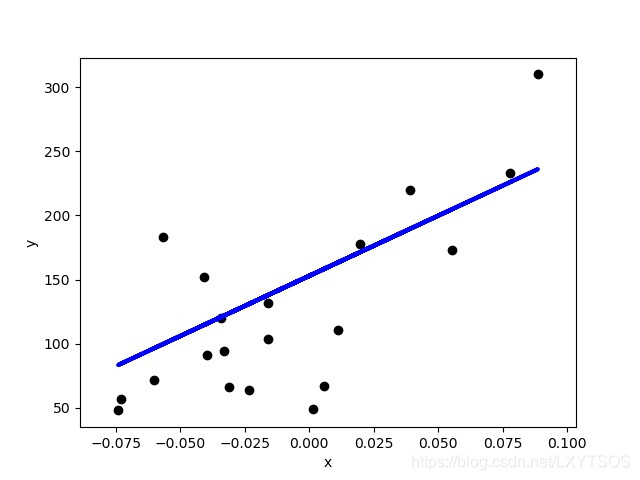
在这里插入图片描述

我们把计算出来的系数（即直线的斜率），均方误差等评估指标打印出来：

Coefficients: 
 [938.23786125]
Mean squared error: 2548.07
Variance score: 0.47

现在大家已经知道线性回归是怎么一回事了，同时也知道如何使用sklearn中提供的算法自己进行尝试了，大家如果碰到类似预测的问题，就可以自己用数据训练模型进行预测啦。

小贴士

为追踪“谷神星”位置，高斯发明了一种方法，根据皮亚齐的观测数据计算出了谷神星的轨道，德国天文学家奥博斯在高斯的预言时间和方位找到了谷神星。1809年，高斯在他的著作《天体运动论》中发表了这种计算方法，这就是最小二乘法。

扫码关注微信公众号：机器工匠，回复关键字“线性回归”获取实现代码。
在这里插入图片描述