1、二分图：
设G=(V,E)是一个图，图的顶点集合可以分为两个集合V1，V2，E中的每个边都有一个点要么属于
点集V1，另一个属于点集V2。
2、二分图的最大匹配：
（1）匹配：一条边就是一个匹配，就是两个点通过一条边来匹配，并且匹配的边的集合中任意两条边都不相连。
（2）最大匹配：一个图能够包含的包含边最多的边的集合。
（3）二分图的最大匹配：二分图中能够包含的最大匹配。
3、二分图的最小顶点覆盖：
（1）定义：二分图的最小顶点覆盖就是（一个点就能覆盖它所在的边），所以二分图的最小顶点覆盖就是
扫描二维码关注公众号，回复：
6534599 查看本文章
选择最少数量的顶点覆盖所有的边。
（2）二分图的最小顶点覆盖 = 二分图的最大匹配。
4、二分图的最大独立集
（1）定义：从二分图中选出一些点，使这些点两两互不相邻。
（2）最大独立集 = 二分图的顶点数量 - 二分图的最小顶点覆盖。
eg（图是盗的）：
下面的二分图中的最小顶点覆盖是V1 = {1,2,4}；
所以二分图的最大独立集V' = V - V1 = {3,5,6,7,8,9};
5、增广路径：
（1）匹配边：与其他边都没有交点的边
（2）交替路径：走过的路径是：非匹配边 -> 匹配边 -> 非匹配边 ->…… ->匹配边 -> 非匹配边；
交替路径中：
一、开始和结尾一定是非匹配边，
二、匹配边的数量 = 非匹配边的数量 - 1；
三、第一个点和最后一个点一定是非匹配点。
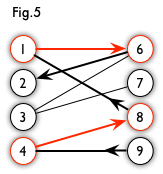
eg：
一个图中的交替路径，红色带箭头为匹配边，黑色带箭头为黑色匹配边
红色的为匹配点，黑色的为非匹配点
（2）增广路径：
从一个未匹配点开始走交替路径得到的增广路径。
（3）增广路径的性质
6、匈牙利算法
（1）功能：通过寻找增广路径求得二分图最大匹配。
（2）基本流程：
（3）性质：
（4）代码实现：
bool dfs(int x){
for(int i=head[x];i!=-1;i=cur[i].nxt){
int y = cur[i].v;
if(vis[y]==0){
vis[y] = 1;
if(pre[y]==-1||dfs(pre[y])){
//pre数组相是记录路径，vis是记录是否被访问到
/*
这里的判断表示判断这点是否为未匹配点（pre[y]==-1），
如果不是未匹配点，假设选择这个点，
然后回溯修改之前的路径如果得到新的未匹配点说明得到了新的匹配路径（dfs(pre[y])）。
*/
pre[y] = x;
return true;
}
}
}
return false;
}
int fun(){
int ans = 0;
memset(pre,-1,sizeof(pre));
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if(dfs(i)) ans++;
//从第i个节点开始判断是否能找到新的增广路径
}
return ans;
//求出的结果就是最大匹配数
}参考文章：
（1）二分图相关概念
（2）匈牙利算法