题目
题目描述
输入格式
输出格式
样例
样例输入
3 4 503 1082 1271 369 303 1135 749 1289 100 54 837 826 947 699 216 389
样例输出
6701
数据范围与提示
题解
做题经历
做到这道题,已经丧心病狂了。
在扎实的语文功底下 $(90/150 pts)$ ,我只用了 $5 min$ 看懂题目.
然后就开始暴搜......
暴搜思路就是,啥都不管,用 $O(2^{2^N})$ 来枚举一个人到底是去打仗还是后勤,然后计算此时的价值,最后输出最大价值即可。
暴搜思路人人懂,算算时间明年到。
时间复杂度大概$O(2^{2^N})$,你以为这样就完了?不,还有个计算的常数 $2^N$,所以完整复杂度 $O(2^{2^N}×2^N)$真是一个友好的算法
正解
基于暴搜,我们可以有一些思考
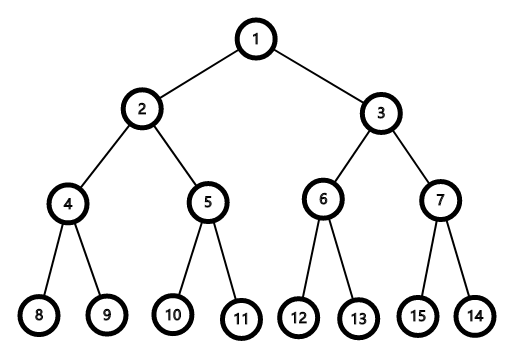
先不考虑 $m$ 的限制。
在这样一棵树里面,平民 $8、9$ 的价值只和他们的所有祖先,也就是 $1、2、4$ 有关
再往上,$4、5$ 的价值只和 $1、2$ 有关
而暴搜复杂度高在何处?
我们做了很多无效的枚举。比如我们要算 $8、9$ 的价值,但是我们却枚举了 $3、5、6、7......$的状态,而这单独对于 $8、9$ 来说,是无效的枚举。
而 $8、9$ 只与他们的祖先有关。
那么我们为什么不考虑一个状态,存下节点编号,以及其祖先状态。
那么一个十分粗糙的状态就出来了:
$dp[s][u]$:节点 $u$ 的祖先状态为 $s$ (二进制串的状压) 时其子树的最大价值。
而这时我们又要考虑 $m$ 对于此题的限制,再加一维:
$dp[s][u][j]$:节点 $u$ 的祖先状态为 $s$ (二进制串的状压) 时,其子树中选了 $j$ 个人去打仗时,这棵子树的最大价值。
那么状转就是:
$dp[s][u][j]=dp[s'][v_1][x]+dp[s'][v_2][y],x+y=j$
这个状转很简单,现在我们来算一下时间复杂度:
首先,对于一个深度为 $k$ 的点
- 其祖先有 $k-1$ 个,那么串 $s$ 有 $2^{k-1}$
- 对于它自己,有两种取值:$1|0$(打仗或者后勤)
- 枚举 $x$ 与 $y$ ,复杂度为$2^{n-k-1}$,有两棵子树,复杂度为${(2^{n-k-1})}^2$
把他们乘起来,时间复杂度$O(2^{k-1}×2×{(2^{n-k-1})}^2)=O(2^{n-k-3})$
但是这个复杂度与 $k$ 有关,不准确,考虑每一层有 $2^{k-1}$ 个节点,那么我们分层计算时间复杂度
每一层的时间复杂度就是 $O(2^{n-k-3}×2^{k-1})=O(2^{2n-4})$
有 $n$ 层,总时间复杂度为 $O(n2^{2n-4})$
时间复杂度有了,似乎不会超时。
开始码代码,但是会发现一个很大的问题:好像这个 $dp$ 数组的空间有点大?
那么我们要省掉一维,哪一维呢?
发现 $s$ 是十分好表示的,我们可以在 $dfs$ 的时候带一个参数 $s$ 来替代掉这一维就可以了。
代码见下:膜拜$trymyedge(lj)$大佬
#include <bits/stdc++.h> #define mz 1000000007 using namespace std; int n, t; int c[1005][15][2], siz[15]; int dp[2005][1005]; int add[1005][2005][2]; void dfs(int x, int y, int z) { if (z == n) { dp[x][0] = max(dp[x][0], add[y][x - t][0]); dp[x][1] = max(dp[x][1], add[y][x - t][1]); } else { for (int i = 0; i <= siz[z]; i++) dp[x * 2][i] = dp[x * 2 + 1][i] = 0; dfs(x * 2, y, z + 1); dfs(x * 2 + 1, y, z + 1); for (int i = 0; i <= siz[z]; i++) for (int j = 0; j <= siz[z]; j++) dp[x][i + j] = max(dp[x][i + j], dp[x * 2][i] + dp[x * 2 + 1][j]); for (int i = 0; i <= siz[z]; i++) dp[x * 2][i] = dp[x * 2 + 1][i] = 0; dfs(x * 2, y + siz[z], z + 1); dfs(x * 2 + 1, y + siz[z], z + 1); for (int i = 0; i <= siz[z]; i++) for (int j = 0; j <= siz[z]; j++) dp[x][i + j] = max(dp[x][i + j], dp[x * 2][i] + dp[x * 2 + 1][j]); } } int main() { int m, x, ans = 0; scanf("%d%d", &n, &m); t = 1 << (n - 1); siz[n - 1] = 1; for (int i = n - 2; i >= 1; i--) siz[i] = siz[i + 1] * 2; for (int i = 0; i < t; i++) for (int j = 0; j < n - 1; j++) scanf("%d", &c[i][j][1]); for (int i = 0; i < t; i++) for (int j = 0; j < n - 1; j++) scanf("%d", &c[i][j][0]); for (int i = 0; i < t; i++) for (int j = 0; j < t; j++) { x = i; for (int k = 0; k < n - 1; k++) { if (x % 2) add[i][j][1] += c[j][k][1]; else add[i][j][0] += c[j][k][0]; x /= 2; } } dfs(1, 0, 1); for (int i = 0; i <= m; i++) ans = max(ans, dp[1][i]); printf("%d\n", ans); return 0; }