本文链接： https://blog.csdn.net/weixin_43972621/article/details/100619631

一、EM算法简介

EM算法全称为Exception Maximization Algorithm，即最大期望算法，以下简称EM算法。它是一种迭代的算法，主要用于含有隐变量的概率参数模型的极大似然和极大后验概率估计。EM算法也经常用于机器学习和计算机视觉的聚类领域，是一个非常重要的算法。

二、EM算法原理

要了解EM算法，就必须先了解极大似然估计，因为整个的EM算法的演算、推导，都是以极大似然估计为基础。

2.1 极大似然估计

2.1.1 两点分布

首先我们来看一个简单的例子：假设我们现在有一个抛硬币的实验，10次抛硬币的结果是：正正反正正正反反正正，记p为每次抛硬币的结果为正的概率，那么这次实验的结果发生的概率记为P：

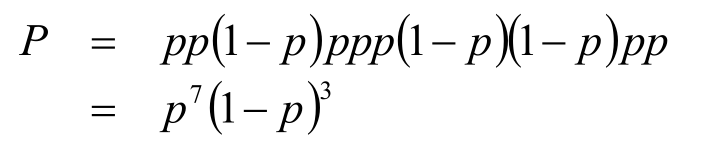
得到了上述的等式，那么当小p取何值时大P能够取得最大值呢？也就是当小p取何值时，这次实验的结果最容易发生。对此我们利用极大似然估计，反过来当大P取最大值时，我们就可以求得此时的小p值。

目标函数：

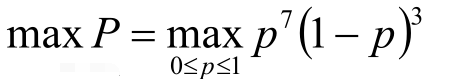
最优解是：

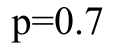
一般形式：

将上述的实验化成一般形式，即假设有X次实验，实验结果的概率为p(x)，分布为 $\overline{p}(x)$ ，则其一般形式为：

2.1.2 高斯分布

进一步考察：

若给定一组样本x1 ,x2 …xn ，已知它们来自于高斯分布N(μ,σ)，试估计参数μ,σ？高斯分布的均值为μ，方差为σ，仍使用刚开始的极大似然估计来求解这个过程。

按照MLE的过程分析：

1.高斯分布的概率密度函数：

2.将Xi的样本值xi带入上述极大似然估计(MLE)的一般形式，得到极大似然函数：

3.化简对数似然函数得到目标函数：

$\sum_{i=1}^{n}\log_{e}\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-(xi-\mu )^2}{2\sigma ^{2}}}$
= $\sum_{i=1}^{n}\log_{e}\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{2\sigma ^{2}}\sum_{i=1}^{n}(xi-\mu )^{^{2}}$
= $-\frac{n}{2}\log_{e}(2\pi \sigma ^{2}) - \frac{1}{2\sigma ^{2}}\sum_{i=1}^{n}(xi-\mu )^{2}$

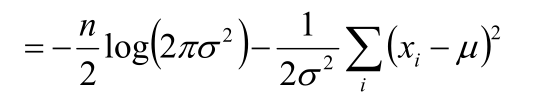
4.将目标函数对参数μ,σ分别求偏导，求极值得到μ,σ的式子：

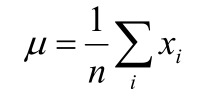
可以对上述的两个公式进行分析：

针对 $\mu =\frac{1}{n}\sum xi$ ，等式右边对所有的样本值求和、取均值，即用样本的均值来代替总体的均值。
针对 $\sigma ^{2} = \frac{1}{n}\sum (xi-\mu )^{2}$ ，等式右边是对样本求方差（真实的方差应该是除n-1，因此称之为伪方差），用样本方差来代替总体的方差。

上述的两个公式是后面分析的基础，可以直接当作结论引用。

2.2 引入隐变量

2.2.1 样本含有隐变量

例子：若在某商场随机挑选100位顾客，测量这100 位顾客的身高，假设这100个样本服从正态分布N(μ,σ)，试估计参数μ,σ。

正态分布的概率密度值已知，又有样本值，结合上述的分析，极大似然估计、求偏导、求极值，联合方程组得到μ,σ。我们也可以直接使用上面的结论直接得到参数μ,σ。

引入隐变量：

若样本中存在男性顾客和女性顾客，服从N(μ1,σ1) 和 N(μ2,σ2)的分布，试估计μ1,σ1，μ2,σ2。

刚刚的样本值是可以直接观察到的，加入隐变量使得样本无法完全观测到。现在只知道身高数据，但是不知道这个身高样本的性别，即不知道每个样本值是来自女性还是男性。针对这种无法完全观察或不完全的数据，用EM算法是很合适的。

2.3 EM算法

2.3.1 混合高斯模型

混合高斯模型求参问题：

将上述的实例再进一步延申，化成更一般的形式，随机变量X是有K个正态分布混合而成，取各个正态分布的概率为π 1 π 2 ... π K ，第i个正态分布的均值为μ i ，标准差为Σ i 。若观测到随机变量X的一系列样本x 1 ,x 2 ,...,x n ，试估计参数 π， μ， Σ。

同理将样本值代入到一般形式，再化简，得到对数似然函数：

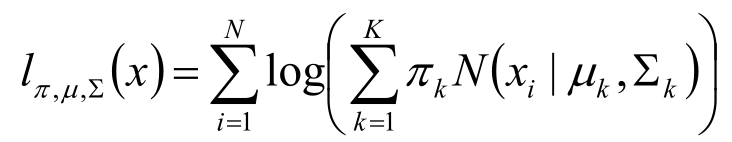
第一步：估算数据来自的组分

估计数据是由每个组分生成的概率，对于每个样本xi，它由第k个组分生成的概率。（这里可能有的讲法不一样，有的说是第k个组分对样本xi的贡献度有多少，但是实质一样的）。

上述公式是EM算法的核心思想， $\pi _{k}N(xi | \mu _{k},\varepsilon _{k})$ 指的是第k个组分对样本xi的贡献度，除分母进行归一化，得到结果 $\gamma (i,k)$ 第i个样本xi来自组分k的概率。

由于式子里的μ,Σ需要我们估计的值，因此采用迭代法，在计算 $\gamma (i,k)$ 的时候假定μ,Σ均已知，即根据先验知识给定μ,Σ, $\pi$ 。

第二步：估计每个组分的参数

将我们的目标函数，取对数化简后得：

$\l _{\pi ,\mu ,\varepsilon } = \sum_{k=1}^{K}\log_{e}(\sum_{k=1}^{K}\pi _{k}N(x_{i}|\mu _{k},\varepsilon _{k}))$

对于组分k而言，可以看做生成了{ $\gamma (i,k)$ * $x_{i}$ | i=1,2,...N}这些点。组分k是一个标准得高斯分布，可以利用上面得公式： $\mu = \frac{1}{n}\sum x_{i}$ 与 $\sigma ^{2} = \frac{1}{n}(x_{i} - \mu )^{2}$ 直接估计出 $\mu _{k}$ , $\varepsilon _{k}$ , $N_{k}$ , $\pi _{k}$ 。
将得到的新的 $\mu _{k}$ , $\varepsilon _{k}$ , $N_{k}$ , $\pi _{k}$ ，再代入回去得到新的 $\mu _{k}$ , $\varepsilon _{k}$ , $N_{k}$ , $\pi _{k}$ 。
反复迭代上述的1，2步直到，收敛到某一可接受的误差值或达到某一设定的迭代次数。

2.3.2 EM算法核心

假定有训练集{ $x_{1}$ ,... $x^{m}$ }，包含有m个独立样本，求该组数据的模型p(x,z)的参数。

通过极大似然估计建立目标函数，取对数化简得到对数似然函数：

这里z是隐随机变量，直接找到参数的估计是很困难的。我们的策略是建立 $\l (\theta )$ 的下界，并且求该下届的最大值，重复该过程直到收敛到局部的最大值。

EM算法的推导过程：

令 $Q_{i}$ 是z的某一个分布， $Q_{i}\geq 0$ ，将样本值代入一般形式，乘一个 $Q_{i}(z^{(i)} )$ 再除一个 $Q_{i}(z^{(i)} )$ ，接着再Jensen不等式的反向利用log函数为凹函数，前面加上负号得到凸函数，再利用凸函数的性质，使其收敛到局部最大值。 $\sum \log \sum_{z^(i)}p(x^{(i)},z^{(i)};\theta )= \sum \log \sum_{z^(i)}Q_{i}(z^{(i)} )\frac{p(x^{(i)},z^{(i)};\theta )}{Q_{i}{(z^(i))}} \geq \sum \sum_{z^(i)}Q_{i}(z^{(i)} )\log \frac{p(x^{(i)},z^{(i)};\theta )}{Q_{i}{(z^(i))}}$
为了使等号成立： $\frac{p(x^{(i)},z^{(i)};\theta )}{Q_{i}(z^{(i)})} = c$ ，因为f(E(x)) = E(f(x))若想等号成立，f(x) = c即f(x)为常函数时等号成立。
进一步分析： $Q_{i}(z^{(i)})\propto p(x^{(i)},z^{(i)};\theta )$ $\sum Q_{i}^{z^{(i)}} = 1$ （因为归一化）联合概率求和得到边缘分布 $Q_{i}^{z^{(i)}} = \frac{p(x^{(i)},z^{(i)};\theta ) }{\sum p(x^{(i)},z^{(i)};\theta)}= \frac{p(x^{(i)},z^{(i)};\theta ) }{ p(x^{(i)};\theta)}=p(x^{(i)}|z^{(i)};\theta )$
最终转化为用给定的样本的隐含变量的条件分布求期望。

三、EM算法框架

该步有点简洁，下次会更新该步...

Repeat until convergence{
    (E-step)For each i,set:
                Qi(z(i)) := p(z(i)|x(i);theat)
    (M-step) Set:
                theat := argmax(objectFunction)

}

四、EM算法优缺点

优点	缺点
聚类	对初始化数据敏感（先验给出的初始均值、方差）
算法计算结果稳定、准确	EM算法计算复杂度高，收敛慢，不适用于大规模、高维度数据
EM算法自收敛，既不需要事先设定类别，也不需要数据间的两两比较合并等操作	当所要优化的函数不是凸函数时，EM算法容易给出局部最优解，而不是全局最优解

五、EM算法案例

针对2.2.1节的案例，某商场的100个样本，并引入隐含变量身高，估计男女样本的均值、方差。如下为程序、图像。

(最大期望)EM算法案例详解