当我说我想了解一下线性回归。。。。

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/LEEANG121/article/details/102755396

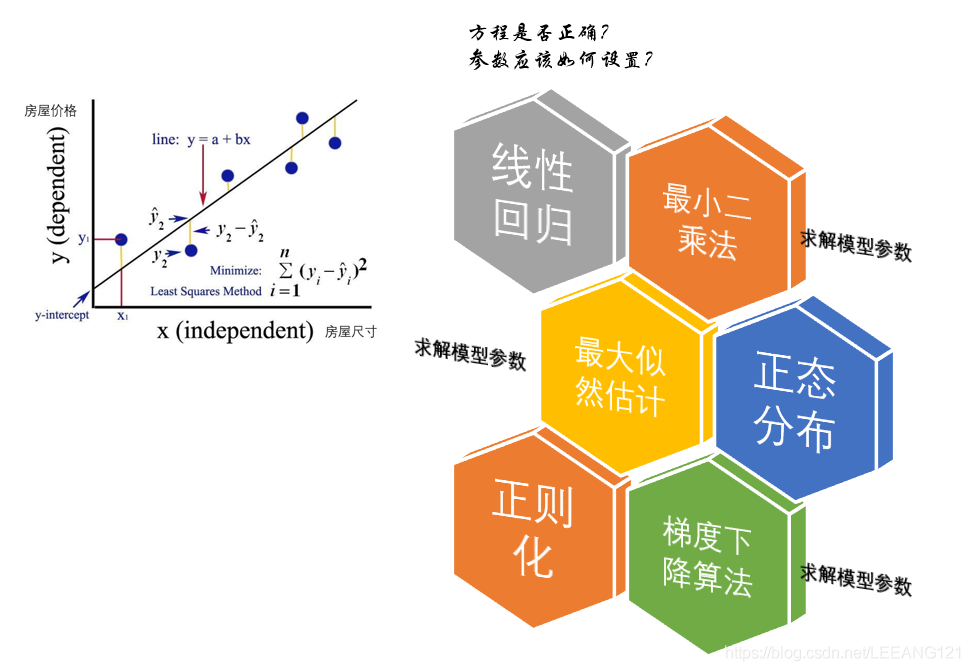
我们学习一门新的知识，或者涉足一个新的领域，往往会发现异常的困难。困难的原因有很多，比如之前对这些领域不熟悉，但是其实还有一个很大的原因就是我们到了一个新的领域想学一个新知识的时候，通常会发现这个新知识背后会有非常多的新知识作为支撑，就好比我们想学会A，结果发现要想理解A，还要了解B,C,D,E…等。比如今天我们谈到的线性回归算法。

本来我们只是想了解线性回归算法，在知道线性回归算法之后我们会考虑这样做到底对不对？于是引出了最小二乘法，但是最小二乘法对不对呢？又引出了最大似然估计。可是最大似然估计里面又提到了正态分布。。。
好不容易搞明白了正态分布，发现方程优化的方法还有正则化、梯度下降等。。。（想死了有没有。。。）
现在就让我们走上这一条学习的不归路吧。。。

线性回归算法

1线性回归模型介绍
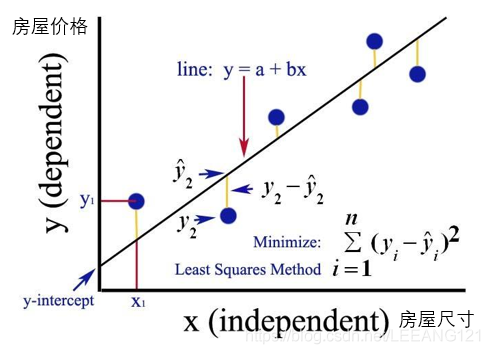
线性回归，就是能够用一个直线较为精确地描述数据之间的关系。这样当出现新的数据的时候，就能够预测出一个简单的值。线性回归中最常见的就是房价的问题。一直存在很多房屋面积和房价的数据。如下图所示：

在这种情况下，就可以利用线性回归构造出一条直线来近似地描述放假与房屋面积之间的关系，从而就可以根据房屋面积推测出房价。

线性回归的函数模型
通过线性回归构造出来的函数一般称之为了线性回归模型。线性回归模型的函数一般写作为：
$y=a+bx$

通过线性回归算法，我们可能会得到很多的线性回归模型，但是不同的模型对于数据的拟合或者是描述能力是不一样的。我们的目的最终是需要找到一个能够最精确地描述数据之间关系的线性回归模型。这是就需要用到代价函数。关于代价函数是个啥，大家可以参考我的博客 啥也不懂照样看懂交叉熵损失函数，简单地说，代价函数就是用来描述线性回归模型与正式数据之前的差异。如果完全没有差异，则说明此线性回归模型完全描述数据之前的关系。如果需要找到最佳拟合的线性回归模型，就需要使得对应的代价函数最小，相关的公式描述如下：
$L(a,b)=\sum_{i}^{n}(y_{i}-(a+b_{x_{i}}))^{2}$
上式中， $a$， $b$是待估计参数， $y_{i}$是真实值。我们对上述公式求导，当导数取到0时，函数的拟合性达到最佳.这种求解方式也叫最小二乘法。那么问题来了，什么是最小二乘法？我们往下继续看。。。

最小二乘法

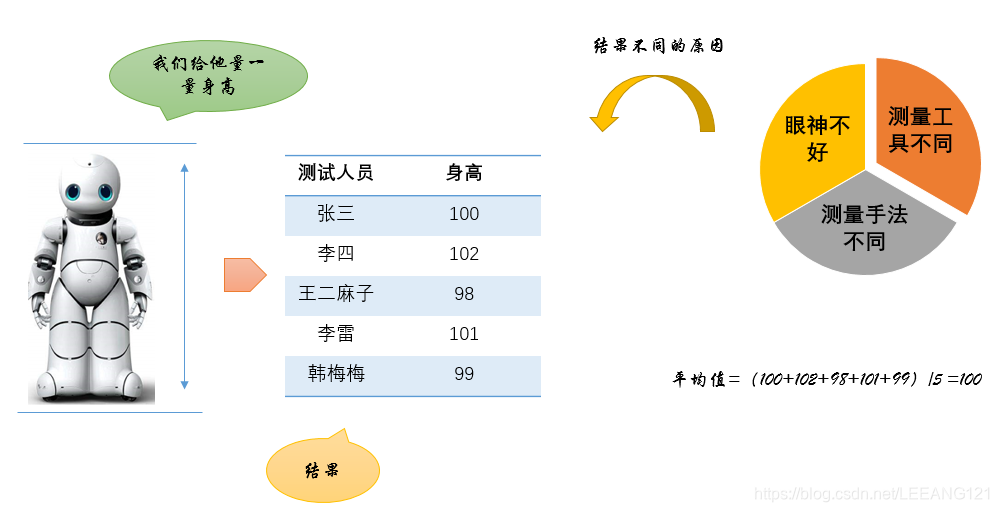
如图所示，假设我们对一个小机器人测量身高，我们请了五个人做这件事情，得到了5个不同的结果。测量结果不一样的原因可能是：
1，这些人眼神不好
2，这些人用的测量工具不同
3，这些人的测量手法不同
总之存在着各种误差，那么我们如何确定这个机器人的最终身高呢？通常我们会把这五个数取平均，我们将这个平均值作为最终的机器人身高。

那么这样做到底行不行呢？

这样做有道理吗？

用调和平均数行不行？

用中位数行不行？

用几何平均数行不行？

现在让我们换一种思路来思考这个问题

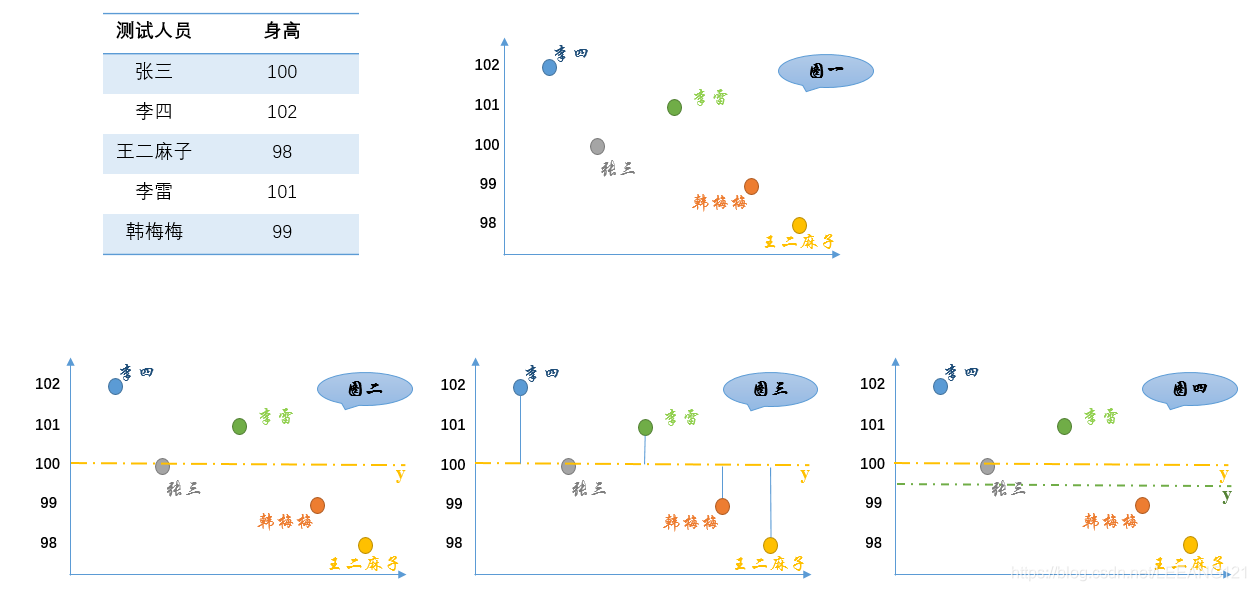
如上图所示：
1,首先，把测试得到的值画在笛卡尔坐标系中（图一）
2,其次，把要猜测的线段长度的真实值用平行于横轴的直线来表示（因为是猜测的，所以用虚线来画），记作 $y$（图二）
3,每个点都向 $y$做垂线，垂线的长度就是 $|y-测量值|$，也可以理解为测量值和真实值之间的误差（图三）
4，这里的 $y$是猜测的值，因此可以不断变化（图四）

法国数学家，阿德里安-馬里·勒讓德（1752－1833，这个头像有点抽象）提出让总的误差的平方最小的 $y$就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动。这里为什么是平房？这是因为有时候误差不能是负数，如果用绝对值表示会很麻烦，因此采用平房的形式。这就是最小二乘法的起源。

误差= $\sum (y-y_{i})^{2}$最小
其中， $y_{i}$代表测量值，我们对上述公式求导，导数为0时最小：
误差=2【( $y$-张三）+（ $y$-李四）+（ $y$-王二麻子）+（ $y$-李雷）+（ $y$-韩梅梅）】 $=0$
$y=(张三+李四+王二麻子+李雷+韩梅梅）/5$
正好是算术平均数。
上面就是最小二乘法，二乘就是平方的意思，台湾也直接翻译成最小平方法。

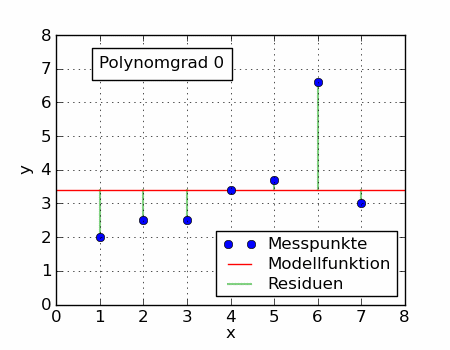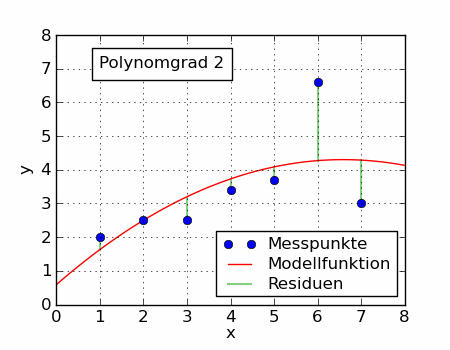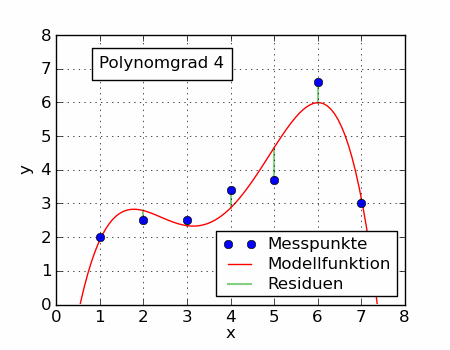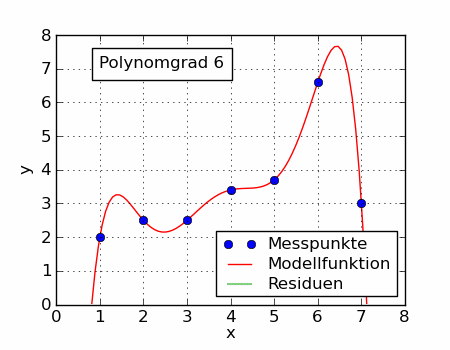
大家看上面动图，当我们使用不同的目标函数时，可以拟合出不同的曲线。前面介绍的算式平均数只是一个特例。

最大似然估计法

历史上总有一些牛逼闪闪的人物对一切事物抱着怀疑的态度，比如我们的数学王子高斯同学。
让我们继续回到之前的问题上面。不管出于什么原因，每次的测量值和真实值总是出现出现一定程度的偏差。我们将这个偏差记为 $\varepsilon$.我们再将出现这个偏差的概率记为 $p(\varepsilon)$.
现在我们假设有这么一个分布函数，里面包含了所有和偏差相关的数据：

$L(x)=p(\varepsilon _{1})+p(\varepsilon _{2})+p(\varepsilon _{3})...=\sum_{i}^{n}p(\varepsilon _{i})$

上述公式就是最大似然函数，其中 $L(x)$成为样本的似然函数。确定最大似然估计量的问题可以归结为微分学中的求解最大值的问题。
我们令 $\frac{d}{d x }L(x )=0$
由于 $L(x)$与 $lnL(x)$在同一个 $x$处取得极值，因此我们也可以去求解
$\frac{d}{d x }lnL(x )=0$
解这个公式会方便很多。

那么这个最大似然估计该如何使用呢？
我们假设 $X\sim N(\mu ,\sigma ^{2})$,其中 $\mu ,\sigma ^{2}$是未知参数，求他们的最大似然估计。
我们先列出 $X$的概率密度
$f(x;\mu ,\sigma ^{2})=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{1}{2\sigma ^{2}}(x-\mu )^{2}]$

这个函数形式是不是很熟悉？ 什么？没有印象了？？

想一想正态分布 没错，我们等下就要介绍正态分布了，但是在这之前，我们先把这个方程搞定吧。

$\mu =\overline{X}$, $\sigma ^{2}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}$

看，是不是很熟悉，原来上面的算术平均数的做法是没有错的。

正态估计

我们先来说一下正什么是正态分布：
若连续型随机变量 $X$的概率密度为 $f(x;\mu ,\sigma ^{2})=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{1}{2\sigma ^{2}}(x-\mu )^{2}]$, $-\infty < x < \infty$
其中 $\mu ,\sigma$为常数，则称 $X$服从参数 $\mu ,\sigma$的正态分布或高斯分布，记为 $X\sim N(\mu ,\sigma ^{2})$。

那么正态分布常见吗？关于这个问题大家可以参考这边文章，写的很形象。
为什么正态分布很常见

正则化

上面我们提到了，我们通过各种手段拟合了一个方程组。但是这个方程组里面的参数该如何设置才能让结果最接近我们的需求呢？前面我们提到了最小二乘法、提到了最大似然估计等。但是当我们在进行机器学习时，会发现，有时候我们更需要我们的模型有一个好的泛化能力，就是说我们更需要这个模型的预测能力强，而非在已知样本里面的拟合度高。可能有点拗口，不用担心，大家可以关注我的另一篇博客白化正则化，真的是白话。。。至于梯度下降算法，我会下次整理。

最后希望这篇文章能够让大家大致了解这些回归算法及他们的关系，若可以帮助到大家，小弟不胜荣幸。