前面我们学习了行列式和矩阵,主要研究了:行列式的计算,包括:2,3阶行列式的计算,n阶行列式的计算;关于矩阵,主要包括:矩阵的线性运算,矩阵的乘法运算,矩阵的转置运算, 矩阵的秩,矩阵可逆的条件及逆阵的求法,分块矩阵及矩阵方程。 初等变换-----最重要和最经常使用的工具。梯形阵, 初等矩阵。
目录
1. n维向量及其线性运算
- 定义1
由数组成的有序数组,称为n维向量,简称为向量。向量通常用斜体希腊字母
等表示。
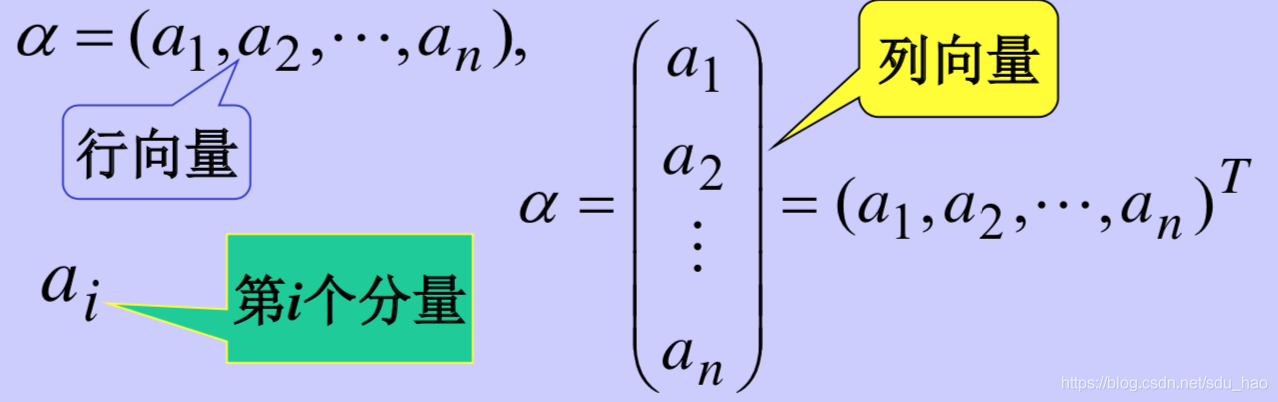

- 定义2
,数值
称为向量
的长度或范数或模,记为
。

- n维向量的线性运算
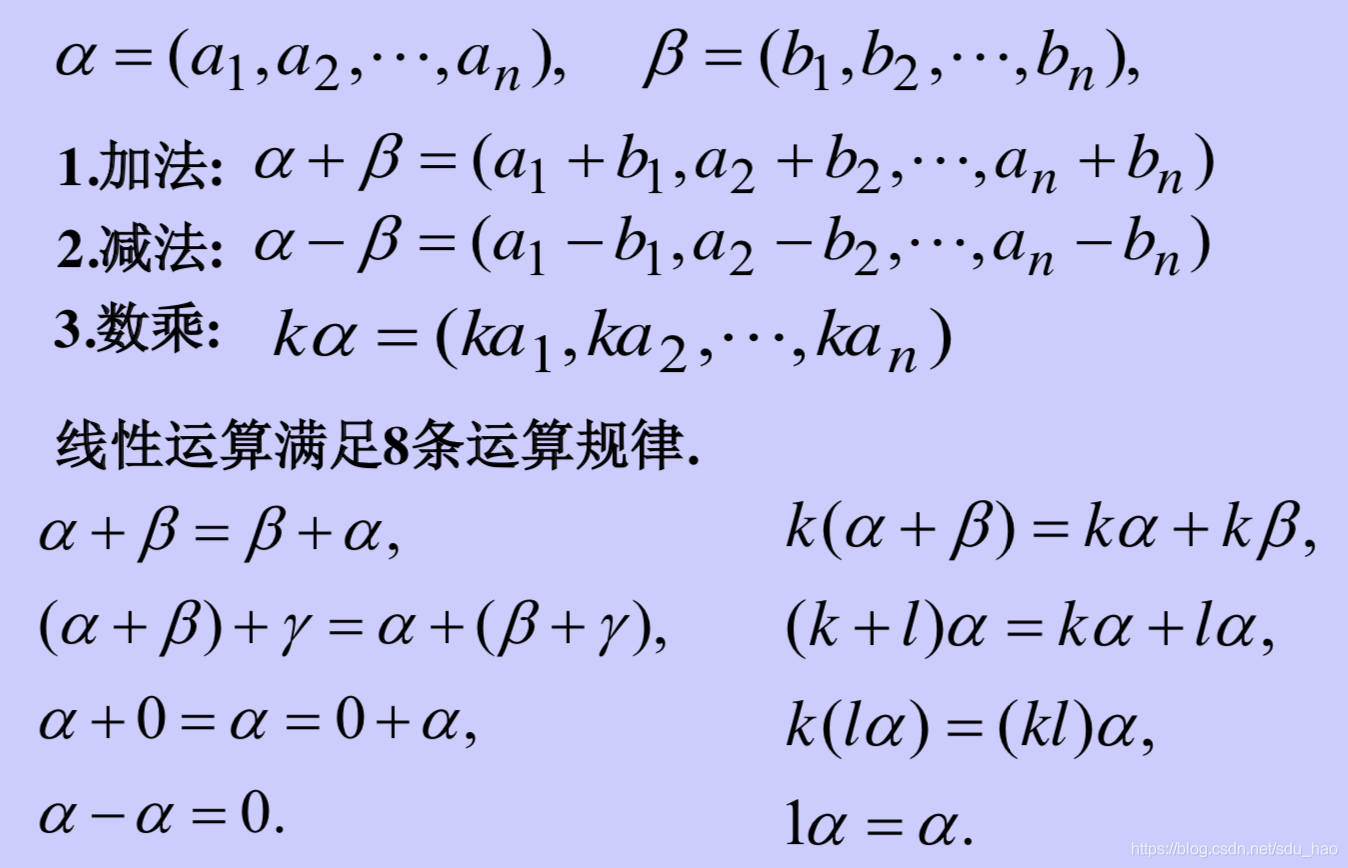
- 线性组合


- 向量组等价


2. 向量组的线性相关
- 定义



让非零向量的系数为0,零向量的系数不为0,存在一组不全为0的数可以使得,所以线性相关。
- 讨论向量组的相关性
系数行列式=0,线性相关:


系数行列式0,说明有唯一零解,线性无关:

3. 相关性判定定理
- 定理1


下面证明唯一性:

- 定理3
在一个向量组中,若有一个部分向量组线性相关, 则整个向量组也必定线性相关,反之不成立。
推论:一个线性无关的向量组的任何非空的部分向量组都 线性无关。
- 定理4


我们已经用三种方法做过上面这个题了:
1)用定义证明,若组合系数不全为0,则线性相关。
2)其中的一个向量,可以用剩余的向量线性表示,则线性相关。
3)将向量组排成矩阵(转换为梯形阵),由矩阵的秩决定。

推论:

- 定理5

4. 相关性判定定理的证明
- 定理4的证明


前m-1行,每一行乘以,加到最后一行。


,m个向量中的部分向量(r+1)线性相关,那么m个向量也线性相关。
- 定理5的证明


5. 向量组的极大无关组和秩
- 极大无关组




- 向量组的秩

- 向量组的等价




6. 向量组极大无关组与秩的求法
- 向量组秩的求法


- 极大无关组的求法
列摆行变换(把向量组摆成矩阵的各个列)




注意一定要列摆行变换,得到矩阵的秩就是向量组的秩。
我们已经看到:用矩阵可以解决向量组的问题,实际上,用向量组也可以解决矩阵的问题。
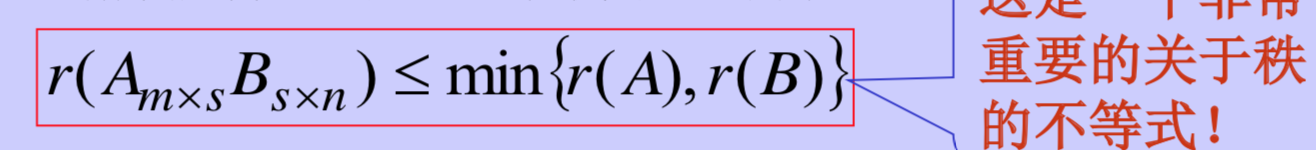
证明:

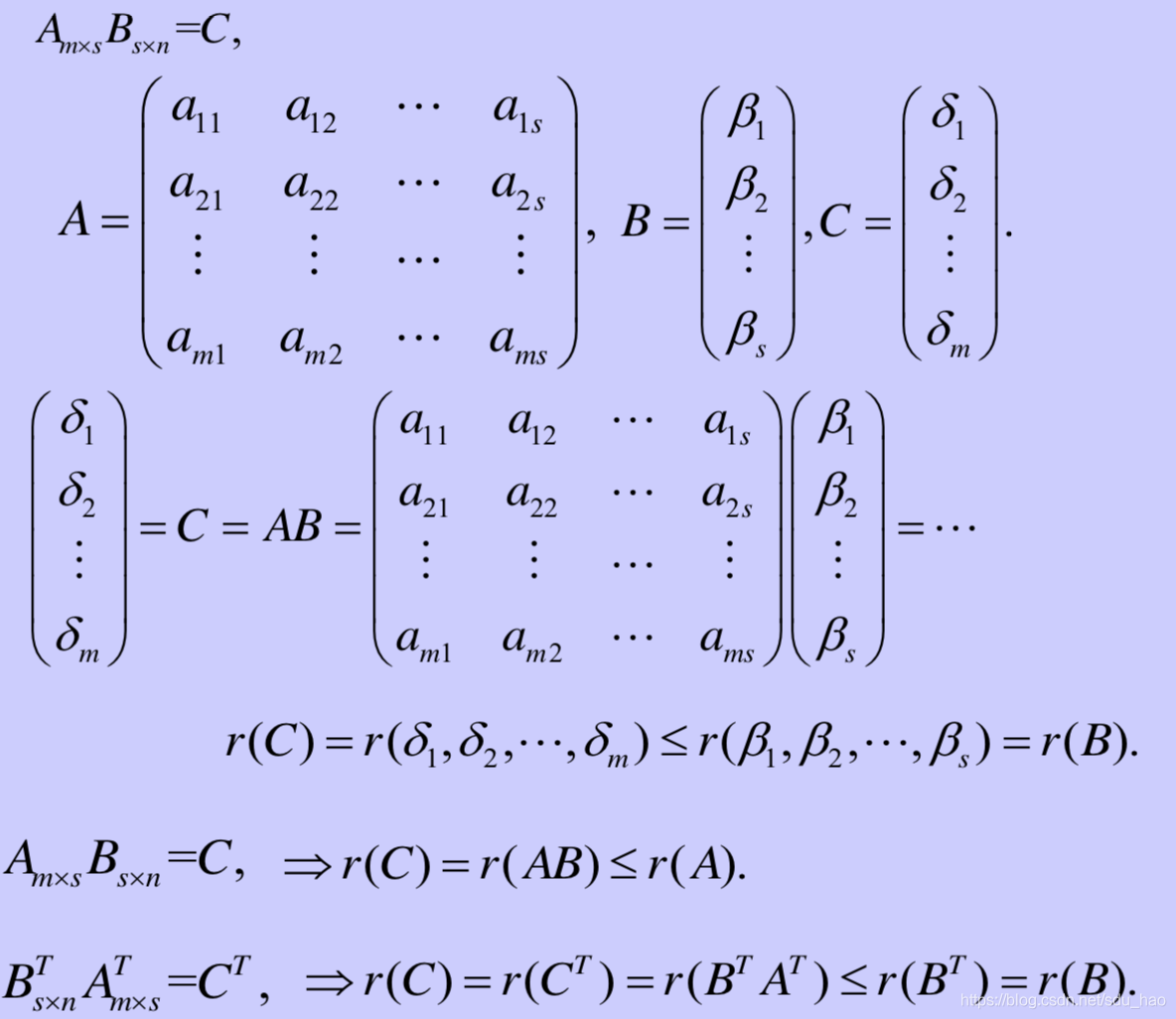
如果一个向量组中的每个向量可以由另一个向量组表示,那么该向量组的秩小于等于另一个向量组的秩。

- 练习
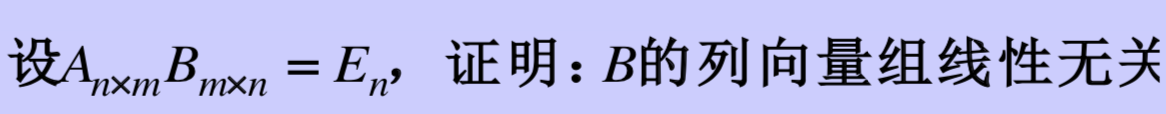
B的列向量线性无关 等价于 B的列向量组的秩为n 等价于 矩阵B的秩为n(列摆行变换)。
7. 向量空间
- 向量空间及其子空间

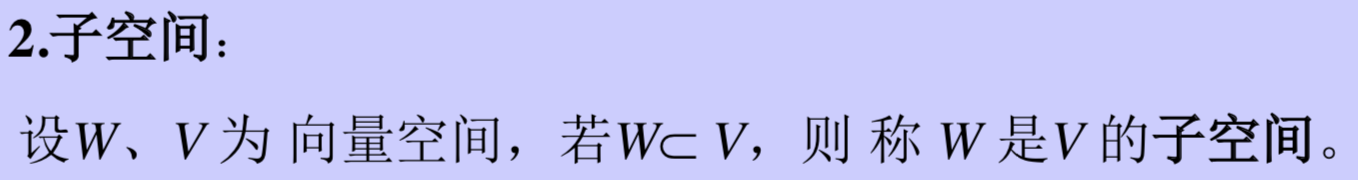
- 向量空间的基与维数



- 向量在基下的坐标



矩阵方程法:

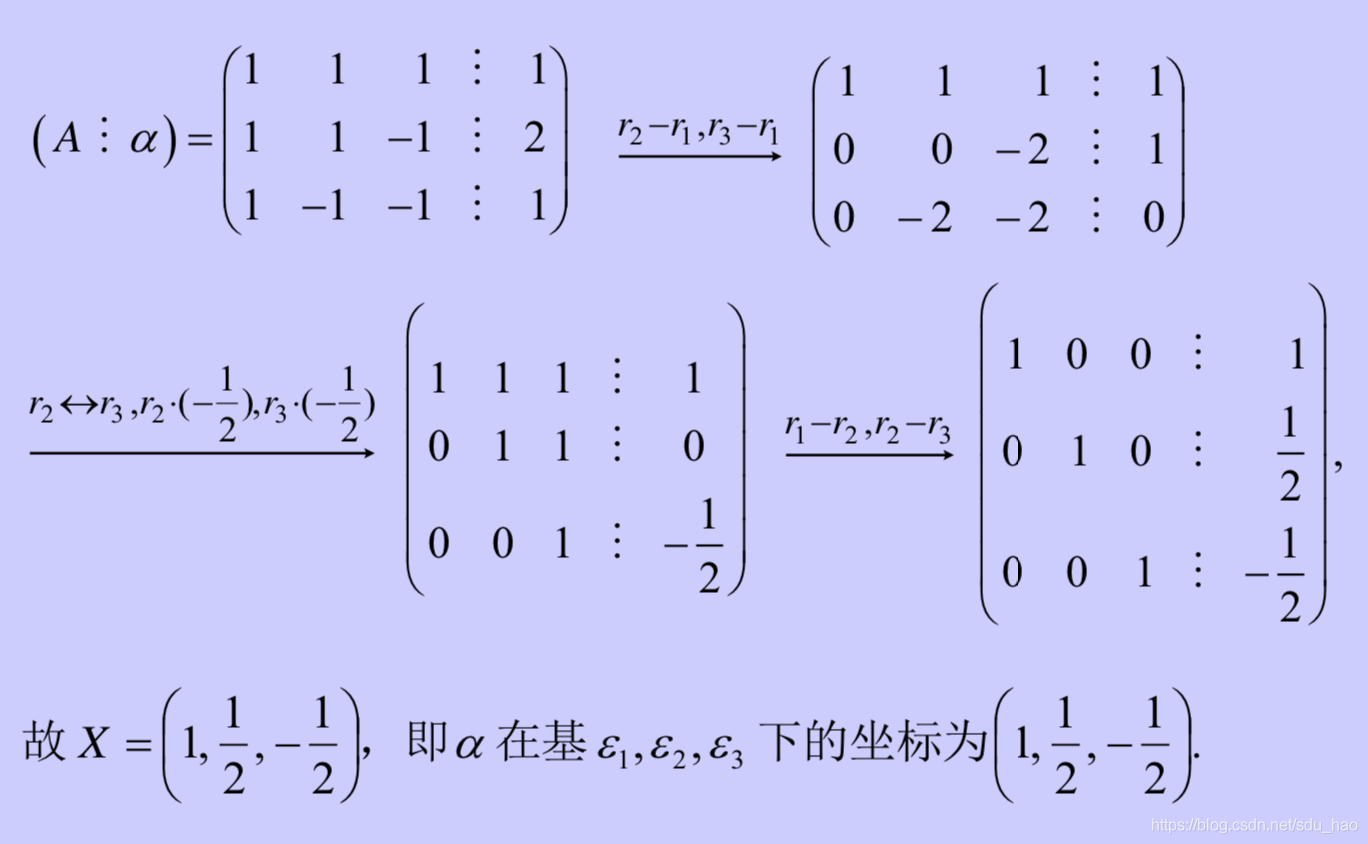
待定系数法:


8. 向量组的正交性
- 向量的内积

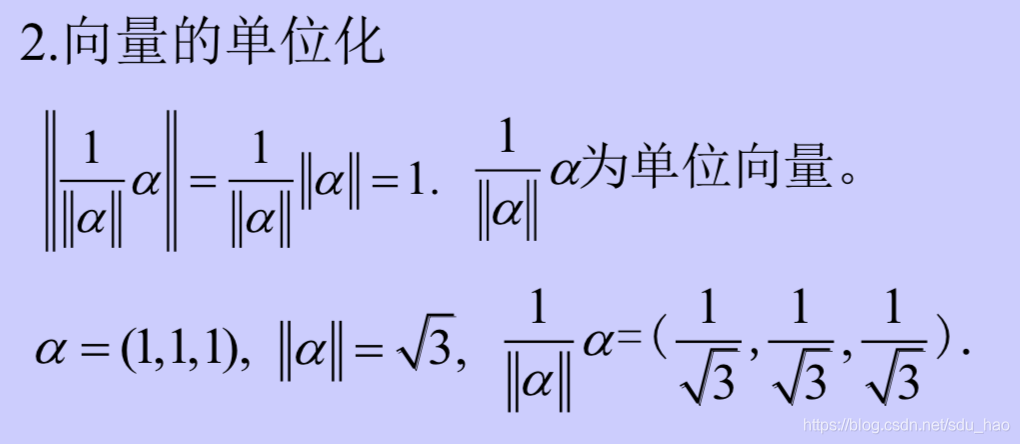
- 向量的夹角
- 向量的正交性


正交向量组一定线性无关向量组,反之不成立。
- 向量组的正交规范化

- 正交矩阵

下面证明列向量组的情形:
