2020张宇1000题·数一·刷题记录
第一篇 高等数学
第1章 极限、连续
二、无穷小比阶(1.47-1.63)
- 通过几种等价替换确定阶数,\(5>n+1>3\),卡正整数的值。
- 分母无理化之后有惊喜,\(tanx-sinx \sim {\frac{1}{2} }x^3\)。
- 多个无穷小量共同作用,看阶数最小的那个。
- 正常等价替换或泰勒,展开原则,式子的和不能为0,阶数取x次数最低的那个。
- ???为什么xlnx不是一阶无穷小?
\(xlnx=x[(1+x)-\dfrac{1}{2}(1+x)^2+o(x^2)]\sim x^?\) - 原式时x的阶无穷小,故原式/x^k的极限存在。(而且一般不为0吧)
- \(\alpha'=cos\ x^2\sim o(x^0);\quad \beta'=2x\ tan\sqrt{x^2}\sim 2o(x^2);\quad \gamma'=\dfrac{1}{2\sqrt x}\ sin\ {\sqrt x}^3\sim \dfrac{1}{2}o(x^1);\)
- 错误做法:\(\lim \limits_{x \to 0}sinx(cosx-4)+3x\sim (x-\dfrac{1}{6}x^3)(1-4)+3x=\dfrac{1}{2}x^3\),
所以3阶无穷小。
直接泰勒展开后(各展开两项)相乘相加,或者相乘后再泰勒展开(各展开三项)相加,最后x的所有低阶都被消去了,只留下一个x的高阶(若剩有多项的话,看x次数最低的那项)。 - (1)提取\(\sqrt2\)出来,往\((1+x)^\alpha -1\sim\alpha x\)上靠。(2)(3)两个等价替换。
- 往\(x-sinx\)上靠,两次\(sinxcosx=\frac{1}{2}sin2x\)。
- 跟1.44看起来有点像,但不是同一种类型。直接泰勒展开,消去1,取x阶数最小的即可,原式~7x^2。答案第二种方法比较麻烦,还有???为啥\(sinxcosxcos2xcos3x=\dfrac{1}{4}sin4xcos3x=\dfrac{1}{8}(sin7x-sinx)\)。
原来是用了三角函数的积化和差公式,另外也复习下和差化积公式: - 提取与等价替换。
- 同上,提取与等价替换,往\(e^x-1\sim x\)上靠。
- 求导与等价替换。
- \(lna-lnb=ln\dfrac{a}{b}\),再拆分与等价替换\(\lim \limits_{f(x) \to 1} ln[f(x)]=\lim \limits_{f(x)-1 \to 0} ln[1+f(x)-1]\sim f(x)-1\)
- 拆分与等价替换。
- 有那种做高考数学题的感觉,计算麻烦,但算出来很爽。先画图理清题意,再根据已知条件构建公式,然后将未知数用式子表达出来。最后再根据同阶,代入极限+保留阶数。

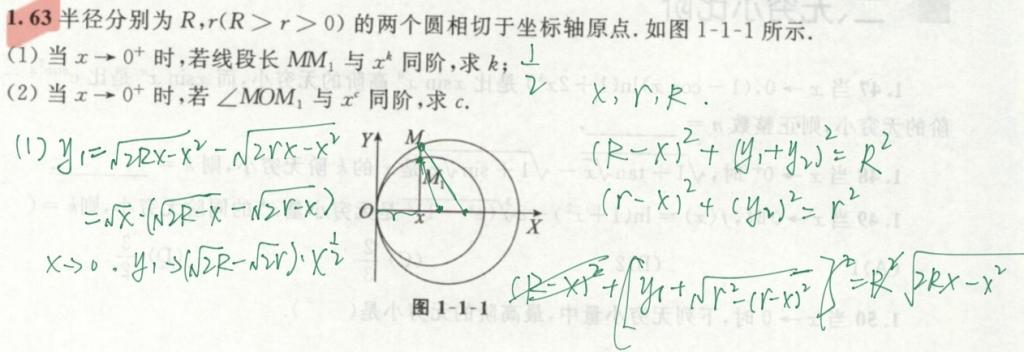

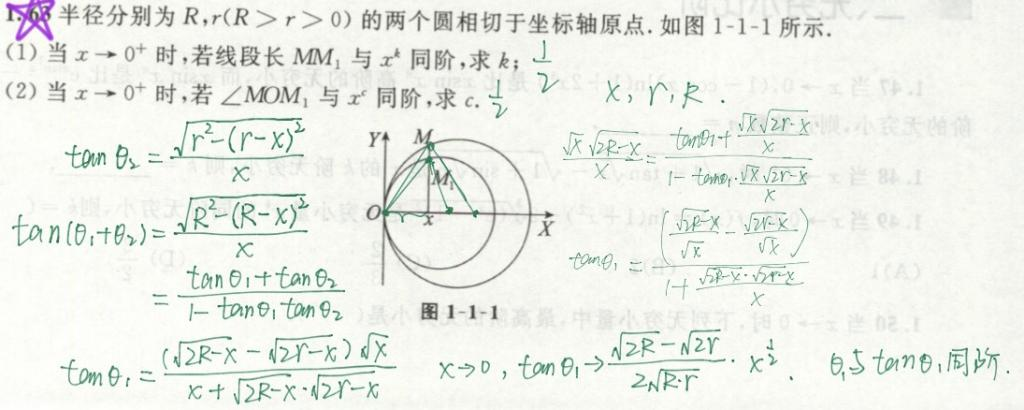
有一点需要注意的,原本47-63的序号在VNote正常显示,发布到博客园网页变成了1-17。= =