原文链接:https://www.cnblogs.com/lfri/p/10329711.html
问题
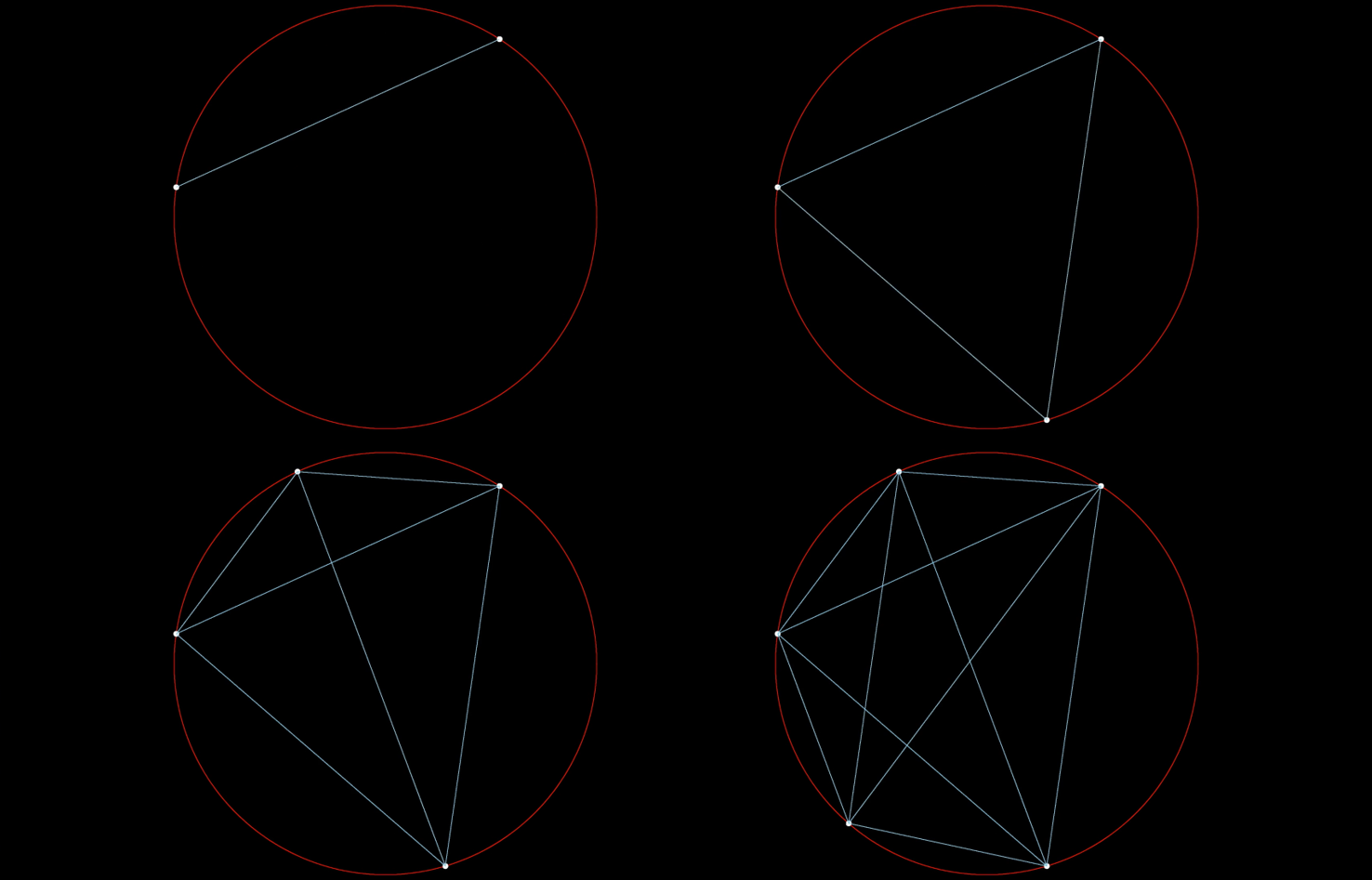
在圆上任取nn个点,将每对点用直线连接起来,并规定任意三条线不能交于同一点,这些直线会将圆分割成多少份?
首先我们列出简单情况来寻找规律:
- 2个点将圆分成2份
- 3个点将圆分成4份
- 4个点将圆分成8份
- 5个点将圆分成16份
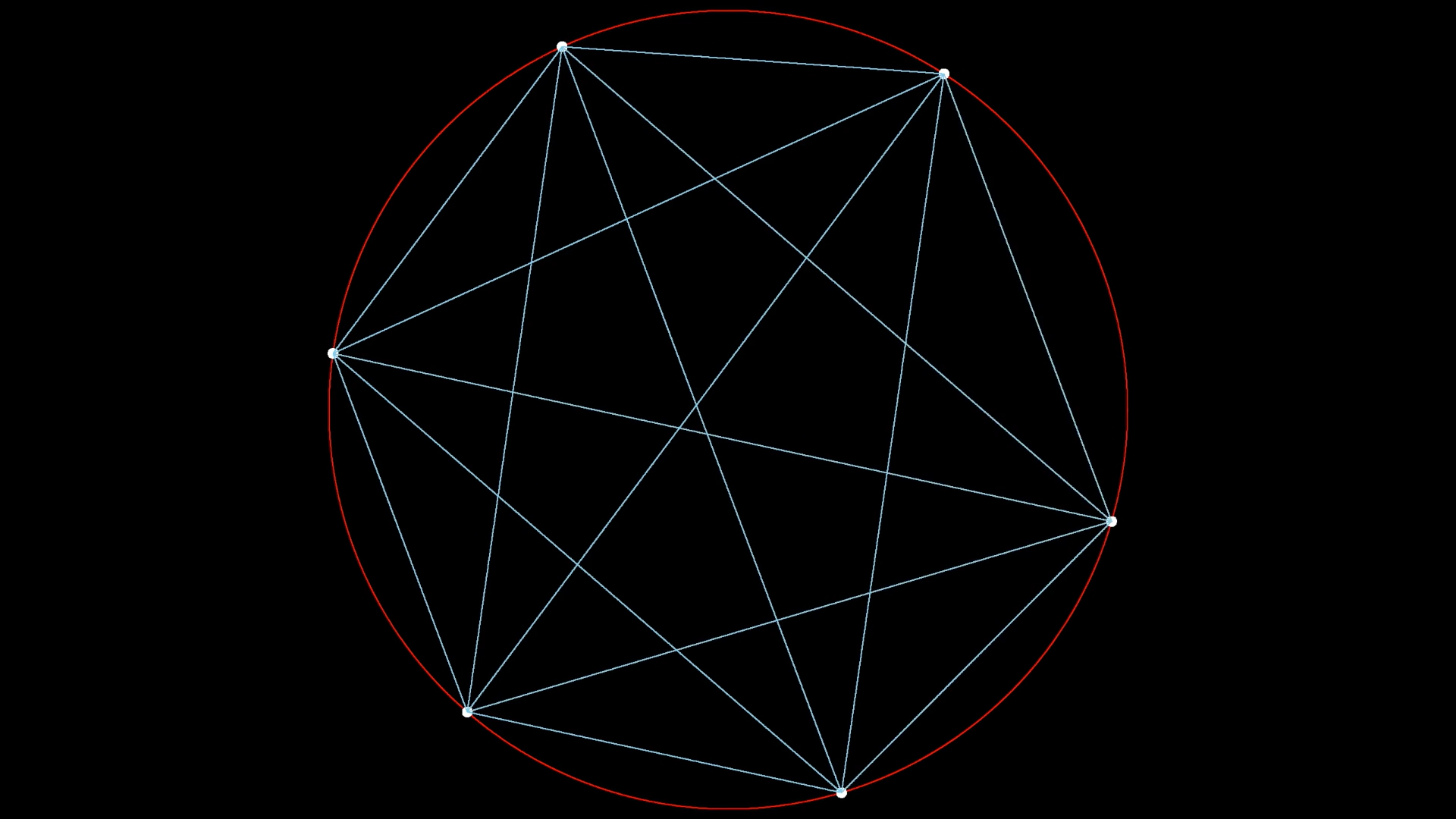
看来这个数列的规律非常明显:每增加一个点,分割的份数都将乘2。然而,当点数增加到6个的时候,分割的份数不是我们预料的32,而是31。
为了找到这个数列的通项公式,我们使用欧拉示性数公式(Euler’s Characteristic Formula)来进行推导:
这个公式的意思是,在任何联通平面简单图中,顶点数减边数加上面数等于2。
为了利用这个公式得到分割的份数(即为面数),我们需要先求出顶点和边的数量。
首先求顶点数:圆内的每个交点都对应圆上的4个点交叉相连,因此圆内的交点共有C4nCn4个,加上圆上的nn个点,因此V=n+C4nV=n+Cn4。
再求边数:圆内的那个交点的度数(度数是与点相连的边的个数)为4,圆上的点都与除此之外的每个点相连,因此度数是n−1n−1,所以总度数为4∗C4n+n∗(n−1)4∗Cn4+n∗(n−1),由于每条边对于总度数的贡献为2,再加上连接圆上顶点的弦的数目,最后得边的数量E=2∗C4n+C2n+nE=2∗Cn4+Cn2+n。
将结果带入欧拉公式,并考虑园外区域也算一个面,则分割的份数为:
由排列组合公式,上式可以继续分解:
这也就解释了当n<6n<6时结果总是成2的幂。
参考链接:
问题
在圆上任取nn个点,将每对点用直线连接起来,并规定任意三条线不能交于同一点,这些直线会将圆分割成多少份?
首先我们列出简单情况来寻找规律:
- 2个点将圆分成2份
- 3个点将圆分成4份
- 4个点将圆分成8份
- 5个点将圆分成16份
看来这个数列的规律非常明显:每增加一个点,分割的份数都将乘2。然而,当点数增加到6个的时候,分割的份数不是我们预料的32,而是31。
为了找到这个数列的通项公式,我们使用欧拉示性数公式(Euler’s Characteristic Formula)来进行推导:
这个公式的意思是,在任何联通平面简单图中,顶点数减边数加上面数等于2。
为了利用这个公式得到分割的份数(即为面数),我们需要先求出顶点和边的数量。
首先求顶点数:圆内的每个交点都对应圆上的4个点交叉相连,因此圆内的交点共有C4nCn4个,加上圆上的nn个点,因此V=n+C4nV=n+Cn4。
再求边数:圆内的那个交点的度数(度数是与点相连的边的个数)为4,圆上的点都与除此之外的每个点相连,因此度数是n−1n−1,所以总度数为4∗C4n+n∗(n−1)4∗Cn4+n∗(n−1),由于每条边对于总度数的贡献为2,再加上连接圆上顶点的弦的数目,最后得边的数量E=2∗C4n+C2n+nE=2∗Cn4+Cn2+n。
将结果带入欧拉公式,并考虑园外区域也算一个面,则分割的份数为:
由排列组合公式,上式可以继续分解:
这也就解释了当n<6n<6时结果总是成2的幂。
参考链接: