基础高等数学的python实现

1.1 函数与极限

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline 
#导入模块

import warnings
warnings.filterwarnings('ignore')
#不发出警告

1.1.1 映射与函数

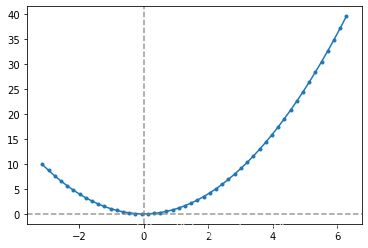
# 基本初等函数：幂函数
# f(x) = x ** a
x = np.linspace(-np.pi, 2*np.pi, num = 50)
y = x ** 2

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

# 辅助线
plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

<matplotlib.lines.Line2D at 0x1149d2470>

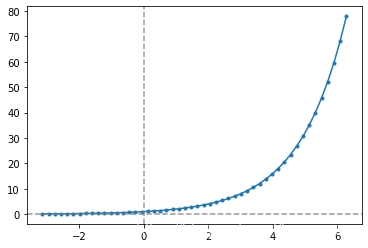
# 基本初等函数：指数函数
# f(x) = a**x

x = np.linspace(-np.pi, 2*np.pi, num = 50)
y = 2**x

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

<matplotlib.lines.Line2D at 0x114a83b38>

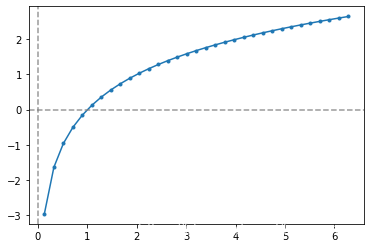
# 基本初等函数：对数函数
# f(x) = loga(x)

x = np.linspace(-np.pi, 2*np.pi, num = 50)
y = np.log2(x)

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

<matplotlib.lines.Line2D at 0x114b31400>

# 基本初等函数：三角函数
# f(x) = sin(ax)

x = np.linspace(-np.pi, 2*np.pi, num = 50)
y = np.sin(x)

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

<matplotlib.lines.Line2D at 0x114b8a470>

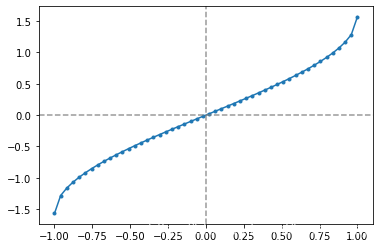
# 基本初等函数：反三角
# f(x) = arcsin(x)

x = np.linspace(-1, 1, num = 50)
y = np.arcsin(x)

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)
#辅助线

<matplotlib.lines.Line2D at 0x114c39d68>

1.1.2 数列

# 一列有序的数
# 数列中的每一个数都叫做这个数列的项
# 排在第一位的数成为这个数列的第一项（首项）
# 排在第n位的数称为这个数列的第n项

s = []
for n in range(1, 11):
    s.append('%i/%i' % (n, n + 1))
s

['1/2', '2/3', '3/4', '4/5', '5/6', '6/7', '7/8', '8/9', '9/10', '10/11']

# 数列的极限 → 如果存在常数 a 对任意给定的正数ε,不论这个数多么小，总存在正整数N，使得当 n>N 时，不等式 |An -a| < ε 都成立，
# 那么常数 a 是数列 {An} 的极限

x = np.arange(50)
y = x/(x + 1)
plt.scatter(x, y, marker = '.')
plt.plot(x, y)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

plt.axhline(1, color = 'red', alpha = 0.6)

<matplotlib.lines.Line2D at 0x114d6ccf8>

1.1.3 函数的极限

# 无穷远处，函数的极限 x → 无穷
# 特定值，函数的极限
# f(x) = x/(x + 1)
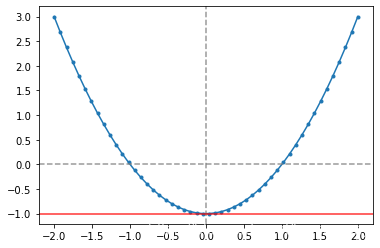
# f(x) = x**2 - 1

x = np.linspace(-2, 2, num = 50)
y = x ** 2 - 1

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

plt.axhline(-1, color = 'red', alpha = 0.8)

<matplotlib.lines.Line2D at 0x114e20a20>

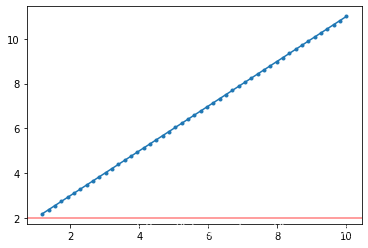
# 练习1
# f(x) = (2*x+1)/x
x = np.arange(50)
y = (2 * x + 1) / x

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

# plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
# plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

plt.axhline(2, color = 'red', linestyle = '--', alpha = 0.5)

<matplotlib.lines.Line2D at 0x114e72860>

# 练习2
# f(x) = (1-x**2)/(1-x)
x = np.linspace(10, 1, num = 50)
y = (1 - x**2)/(1 - x)

plt.scatter(x, y, marker = '.')
plt.plot(x, y)

plt.axhline(2, color = 'red', alpha = 0.5)

<matplotlib.lines.Line2D at 0x114f265c0>

1.2.1 导数

# 直线运动问题
# 对于f(X) = x**2

def f(x):
    return x**2

plt.figure(figsize = (12, 6))
n = np.linspace(-10, 10, num = 50)
plt.plot(n, f(n))
plt.xlim(-11, 11)
plt.ylim(-10, 110)

# 选中曲线上两个点
plt.plot([2,5], [4, 25], color = 'r')
print('直线斜率为%.2f' % ((25 - 4)/(5 - 2)))
print('-------------')

直线斜率为7.00
-------------

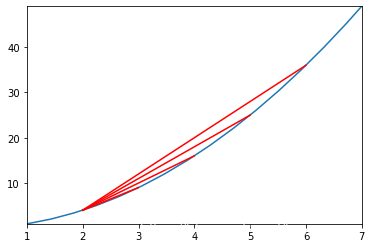
# 求m的导数
x_m = 2
y_m = f(x_m)
plt.plot(n, f(n))
plt.xlim(1, 7)
plt.ylim(1, 49)

for i in range(4, 0, -1):
    plt.plot([x_m, x_m + i], [y_m, f(x_m + i)], color = 'r')
    print('直线斜率为%.2f' % ((f(x_m + i) - y_m)/(x_m + i - x_m)))

    

直线斜率为8.00
直线斜率为7.00
直线斜率为6.00
直线斜率为5.00

def ds(xm, n):
    '''
    该函数为求f(x) = x**2的导数
    xm：m点的x值
    n：m点x往右偏移的距离
    函数最后导出
    '''
    y1 = f(xm)
    y2 = f(xm + n)
    return (y2 - y1)/n

for i in np.linspace(1, 0, num = 1000,endpoint  = False):
    print('偏移%.3f个单位距离时，斜率为：%.5f' % (i, ds(2, i)))
# 斜率为4
# 切线函数为：y = 4*x - 4

偏移1.000个单位距离时，斜率为：5.00000
偏移0.999个单位距离时，斜率为：4.99900
偏移0.998个单位距离时，斜率为：4.99800
.
.
.
.
偏移0.003个单位距离时，斜率为：4.00300
偏移0.002个单位距离时，斜率为：4.00200
偏移0.001个单位距离时，斜率为：4.00100

# 图示
n = np.linspace(-10, 10, num = 50)
plt.plot(n, f(n))
plt.xlim(-11, 11)
plt.ylim(-10, 110)
plt.scatter(2, 4)
plt.plot(n, 4*n - 4)

[<matplotlib.lines.Line2D at 0x115610cc0>]

def f(x):
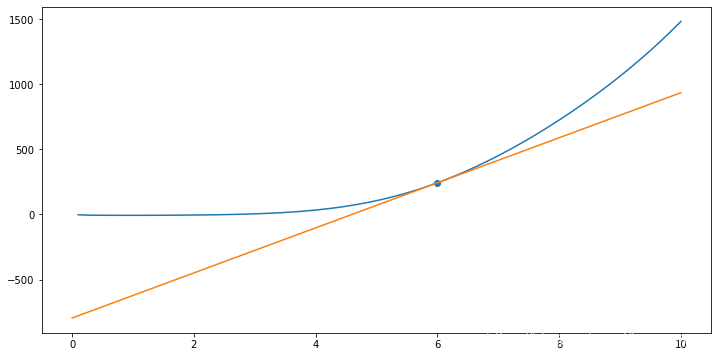
    return 2*x**3 - 5*x**2 + 3*x*np.sin(x) + (x**2 + 1)/(2 * x) - 7

x = np.linspace(0, 10, num = 100)
y = f(x)
plt.figure(figsize = (12, 6))
# plt.scatter(x, y)
plt.plot(x, y)


def f_(x):
    return 1 - 10 * x + 6 * x**2 - (1 + x**2)/(2 * x**2) + 3*np.cos(x)*x + 3*np.sin(x)

m = 6
ym = f(6)
print(m, ym)
plt.scatter(m, ym)

k = f_(6)
b = ym - m*k

def fk(x):
    return k * x + b

yk = fk(x)
plt.plot(x, yk)

6 243.05385436575267





[<matplotlib.lines.Line2D at 0x1153457b8>]

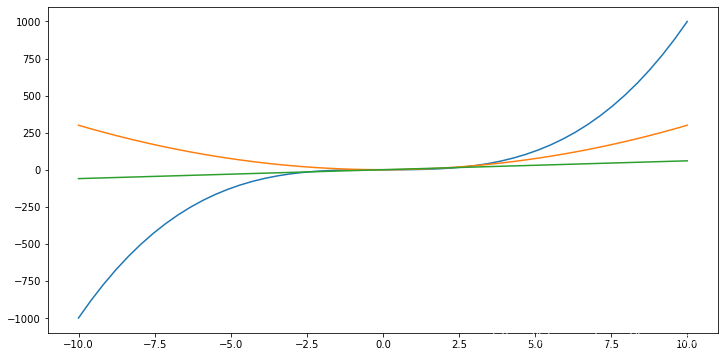
def f2(x):
    return x**3
def f2_(x):
    return 3 * x**2
def f2__(x):
    return 6 * x
plt.figure(figsize = (12, 6))
x = np.linspace(-10, 10, num = 50)
y1 = f2(x)
plt.plot(x, f2(x))
plt.plot(x, f2_(x))
plt.plot(x, f2__(x))

[<matplotlib.lines.Line2D at 0x1153595c0>]

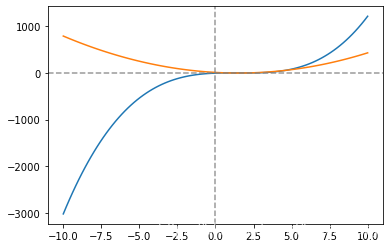
1.3.2 函数的单调性与曲线的凸凹性

# f(X) = 2 * x**3 - 9 * x**2 + 12 * x - 3
def f1(x):
    return 2 * x**3 - 9 * x**2 + 12 * x - 3
def f1_1(x):
    return 6 * x**2 - 18 * x + 12

n = np.linspace(-10, 10, num = 100)
plt.plot(n, f1(n))
plt.plot(n, f1_1(n))

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

# 辅助线

#plt.xlim([-1,3])
#plt.ylim([-20,20])
# 查看x在[-1,3]区间的情况
# f1_(x) = 0时，x为1或2

# 结论：设函数y = f(x)在[a,b]上连续，在(a,b)内可导 
# → 
# 若函数导数始终大于等于0，该函数单调增加；反之单调减少

<matplotlib.lines.Line2D at 0x1157335f8>

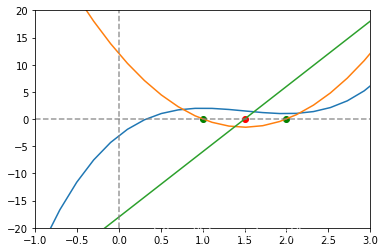
# 二阶导数

def f1_2(x):
    return 12 * x - 18

n = np.linspace(-10, 10, num = 100)
plt.plot(n, f1(n))
plt.plot(n, f1_1(n))
plt.scatter([1, 2], [0, 0], color = 'green')

plt.plot(n, f1_2(n))
plt.scatter([1.5], [0], color = 'red')
plt.xlim([-1, 3])
plt.ylim([-20, 20])
plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

<matplotlib.lines.Line2D at 0x115d57fd0>

1.3.3 方程近似解

# 二分法求解
# 对于函数f(x) = x**3 + 1.1*x**2 + 0.9*x -1.4
# 单调递增
def f2(x):
    return x**3 + 1.1 * x**2 + 0.9*x - 1.4
def f2_1(x):
    return 3 * x**2 + 2.2 * x + 0.9

n = np.linspace(-10, 10, num = 100)
plt.plot(n, f2(n))
plt.plot(n, f2_1(n))
plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

<matplotlib.lines.Line2D at 0x115e2ed30>

# 二分法求解

lst = [0, 1]
n = 0
while n < 30:
    z = (lst[0] + lst[1])/2
    if f2(z) * f2(0) > 0:
        lst[0] = z
    else:
        lst[1] = z
    print('第%i次迭代的隔离区间为' % (n + 1), lst)
    n+=1

第1次迭代的隔离区间为 [0.5, 1]
第2次迭代的隔离区间为 [0.5, 0.75]
第3次迭代的隔离区间为 [0.625, 0.75]
第4次迭代的隔离区间为 [0.625, 0.6875]
第5次迭代的隔离区间为 [0.65625, 0.6875]
第6次迭代的隔离区间为 [0.65625, 0.671875]
第7次迭代的隔离区间为 [0.6640625, 0.671875]
第8次迭代的隔离区间为 [0.66796875, 0.671875]
第9次迭代的隔离区间为 [0.669921875, 0.671875]
第10次迭代的隔离区间为 [0.669921875, 0.6708984375]
第11次迭代的隔离区间为 [0.67041015625, 0.6708984375]
第12次迭代的隔离区间为 [0.670654296875, 0.6708984375]
第13次迭代的隔离区间为 [0.670654296875, 0.6707763671875]
第14次迭代的隔离区间为 [0.670654296875, 0.67071533203125]
第15次迭代的隔离区间为 [0.670654296875, 0.670684814453125]
第16次迭代的隔离区间为 [0.670654296875, 0.6706695556640625]
第17次迭代的隔离区间为 [0.670654296875, 0.6706619262695312]
第18次迭代的隔离区间为 [0.670654296875, 0.6706581115722656]
第19次迭代的隔离区间为 [0.6706562042236328, 0.6706581115722656]
第20次迭代的隔离区间为 [0.6706571578979492, 0.6706581115722656]
第21次迭代的隔离区间为 [0.6706571578979492, 0.6706576347351074]
第22次迭代的隔离区间为 [0.6706571578979492, 0.6706573963165283]
第23次迭代的隔离区间为 [0.6706572771072388, 0.6706573963165283]
第24次迭代的隔离区间为 [0.6706572771072388, 0.6706573367118835]
第25次迭代的隔离区间为 [0.6706573069095612, 0.6706573367118835]
第26次迭代的隔离区间为 [0.6706573069095612, 0.6706573218107224]
第27次迭代的隔离区间为 [0.6706573069095612, 0.6706573143601418]
第28次迭代的隔离区间为 [0.6706573106348515, 0.6706573143601418]
第29次迭代的隔离区间为 [0.6706573106348515, 0.6706573124974966]
第30次迭代的隔离区间为 [0.6706573106348515, 0.670657311566174]

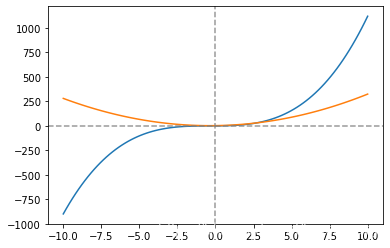
def f2_2(x):
    return 6*x + 2.2

xmin = -0.2
xmax = 1.2
n = np.linspace(xmin, xmax, num = 100)
plt.plot(n, f2(n))
plt.xlim([xmin, xmax])
plt.ylim([f2(xmin), f2(xmax)])
plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axvline(1, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

xn = 1
lst_k = []
for i in range(5):
    def f2_qx(xi):
        k = f2_1(xn)
        b = f2(xn) - k * xn
        return k * xi + b
    plt.plot(n, f2_qx(n))
    xn = xn - f2(xn)/f2_1(xn)
    print('第%i次的迭代近似值为' %i,xn)

第0次的迭代近似值为 0.7377049180327868
第1次的迭代近似值为 0.6741688116739283
第2次的迭代近似值为 0.6706675755945111
第3次的迭代近似值为 0.6706573108138408
第4次的迭代近似值为 0.6706573107258098

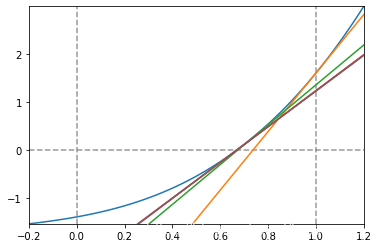
1.5.2 定积分的求解

# 计算定积分
def f(x):
    return x**2

n = np.linspace(-1, 2, num = 50)
n1 = np.linspace(0, 1, num = 50)
plt.plot(n, f(n))
plt.fill_between(n1, 0, f(n1), color = 'k', alpha = 0.4)
plt.xlim(-1, 2)
plt.ylim(-1, 5)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axvline(1, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

area = 0
xi = 0
for i in range(len(n1))[:-1]:
    xi = (n1[i] + n1[i + 1])/2
    area += (n1[i + 1] - n1[i]) * f(xi)
print(area)

0.33329862557267803

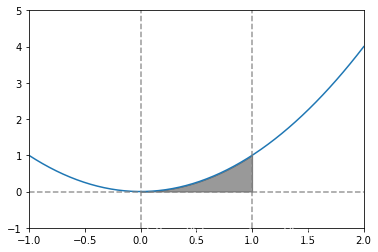
1.5.3 定积分的应用

# 计算图形的面积
def f11(x):
    return (2*x)**0.5
def f12(x):
    return -(2*x)**0.5
def f2(x):
    return x - 4

n = np.linspace(10, -2, num = 100)
plt.plot(n, f2(n))

n1 = n[n >= 0]
plt.plot(n1, f11(n1))
plt.plot(n1, f12(n1))
plt.xlim(-2, 10)
plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)

y = np.linspace(-2, 4, num = 100)
area = 0
for i in range(len(y))[:-1]:
    y_ = y[i + 1] - y[i]
    area += y_ * (y[i + 1] + 4 - y[i + 1]**2/2)
print(area)

17.998163452708912

def f(x):
    return (x + np.sin(x))/(1 + np.cos(x))

n = np.linspace(-1, 0.8*np.pi, num = 50)
n1 = np.linspace(0, 0.5*np.pi, num = 50)
plt.plot(n, f(n))
plt.fill_between(n1, 0, f(n1), color = 'k', alpha = 0.4)
plt.xlim(-1, 0.8*np.pi)
plt.ylim(-1, 4)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axvline(0.5 * np.pi, color = 'gray', linestyle = '--', alpha = 0.8)

area = 0
xi = 0
for i in range(len(n1))[:-1]:
    xi = (n1[i] + n1[i + 1])/2
    area += (n1[i + 1] - n1[i]) * f(xi)
print(area)

1.570686266967039

def f(x):
    return (1 - np.sin(2*x))**0.5
n = np.linspace(-1, 0.4*np.pi, num = 50)
n1 = np.linspace(0, 0.25*np.pi, num = 50)
plt.plot(n, f(n))
plt.fill_between(n1, 0, f(n1), color = 'k', alpha = 0.4)
plt.xlim(-0.5, 0.4*np.pi)
plt.ylim(-1, 2)

plt.axvline(0, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axvline(0.25*np.pi, color = 'gray', linestyle = '--', alpha = 0.8)
plt.axhline(0, color = 'gray', linestyle = '--', alpha = 0.8)

area = 0
xi = 0
for i in range(len(n1))[:-1]:
    xi = (n1[i] + n1[i + 1])/2
    area += (n1[i + 1] - n1[i])*f(xi)
print(area)

0.4142179964572354

1.6 重积分

from mpl_toolkits.mplot3d import axes3d

x = np.linspace(-np.pi, np.pi, num = 50)
y = np.linspace(-np.pi, np.pi, num = 50)
x, y = np.meshgrid(x, y)
z = np.sin(x + y)
fig = plt.figure(figsize = (15, 12))
ax = fig.gca(projection = '3d')
ax.view_init(elev = None, azim = None)
# view_init → 设置视角，elev为z平面的角度，azim为xy平面的角度

ax.plot_surface(x, y, z, rstride = 2, cstride = 2, cmap = 'Blues', alpha = 0.7)

<mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x11643b4a8>

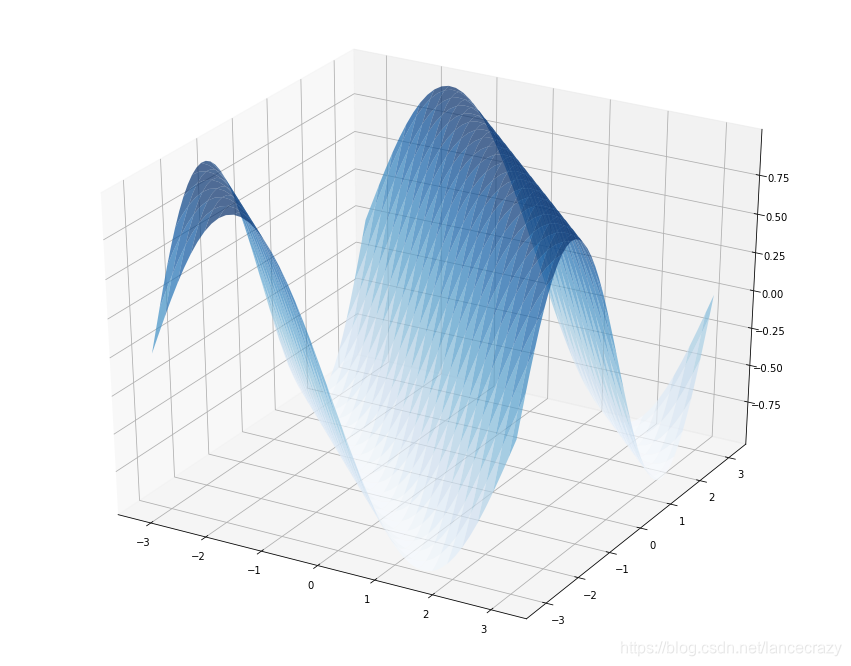
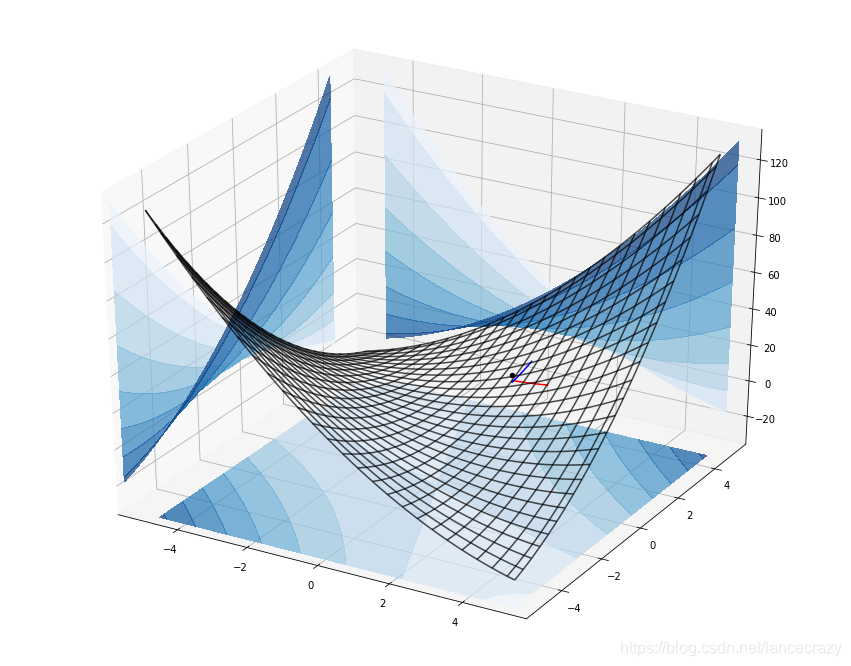
x = np.linspace(-5, 5, num = 50)
y = np.linspace(-5, 5, num = 50)
x, y = np.meshgrid(x, y)
z = x**2 + 3*x*y + y**2

fig = plt.figure(figsize = (15, 12))
ax = fig.gca(projection = '3d')
ax.view_init(elev = None, azim = None)

ax.plot_wireframe(x, y, z, rstride = 2, cstride = 2, color = 'k', alpha = 0.7)
ax.contourf(x, y, z, zdir = 'z', offset = -40, cmap = 'Blues', alpha = 0.7)
ax.contourf(x, y, z, zdir = 'x', offset = -6, cmap = 'Blues', alpha = 0.7)
ax.contourf(x, y, z, zdir = 'y', offset = 6, cmap = 'Blues', alpha = 0.7)

ax.scatter(1, 2, 11, s = 20, c = 'k')

def fxz(x):
    return 2**x + 6
xn1 = np.linspace(1, 2, num = 20)
yn1 = np.ones_like(xn1) * 2
zn1 = fxz(xn1)
ax.plot(xn1, yn1, zn1, '-r')

def fyz(y):
    return 2**y + 3
yn2 = np.linspace(2, 3, num = 20)
xn2 = np.ones_like(xn1) * 1
zn2 = fyz(yn2)
ax.plot(xn2, yn2, zn2, '-b')

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x11a479898>]