Python——EM(期望极大算法)实战(附详细代码与注解)(一)

开始之前

各位朋友大家好！今天我将带大家撸EM算法代码，在撸之前(呵呵，可别乱想≧◔◡◔≦)，我们首先讲清楚什么是EM算法？为什么要用EM算法？。在这里我简要的介绍一下，大家都知道极大似然估计吧（至少读研的同学和学概率的同学都有了解），那就是先把对数似然函数表达式列出，再通过求导得到参数θ的极大或极小值。但是问题来了，显示问题中并非所有问题都是一眼能看出它是某个因素导致的，或许它可能是通过间接因素导致的。这就引出了隐变量的概念，所以EM算法就是含有隐变量的概率模型的极大似然估计。关于EM算法的知识大家可以查阅相关资料，也可以看我之前写的博文EM算法。

前提准备

Jupyter notebook 或 Pycharm
火狐浏览器或谷歌浏览器
win7或win10电脑一台
网盘提取csv数据

需求分析

给定一些数据(5000条)，运用高斯模型进行建模(为什么用高斯模型，因为自然界中大多数事物都服从高斯分布)，写出Log函数，再运用EM算法求出使Log函数取最大的参数θ。

【小小建议】：看代码时最好先从main入口开始看，当看到某个函数的调用时再回过头来看这个函数的定义。有什么问题可以在下面评论处书写，很愿意与您探讨(>‿◠)✌
python代码如下：

import numpy as np
from scipy.stats import multivariate_normal  #多元正态分布
from numpy import genfromtxt    #数据处理函数

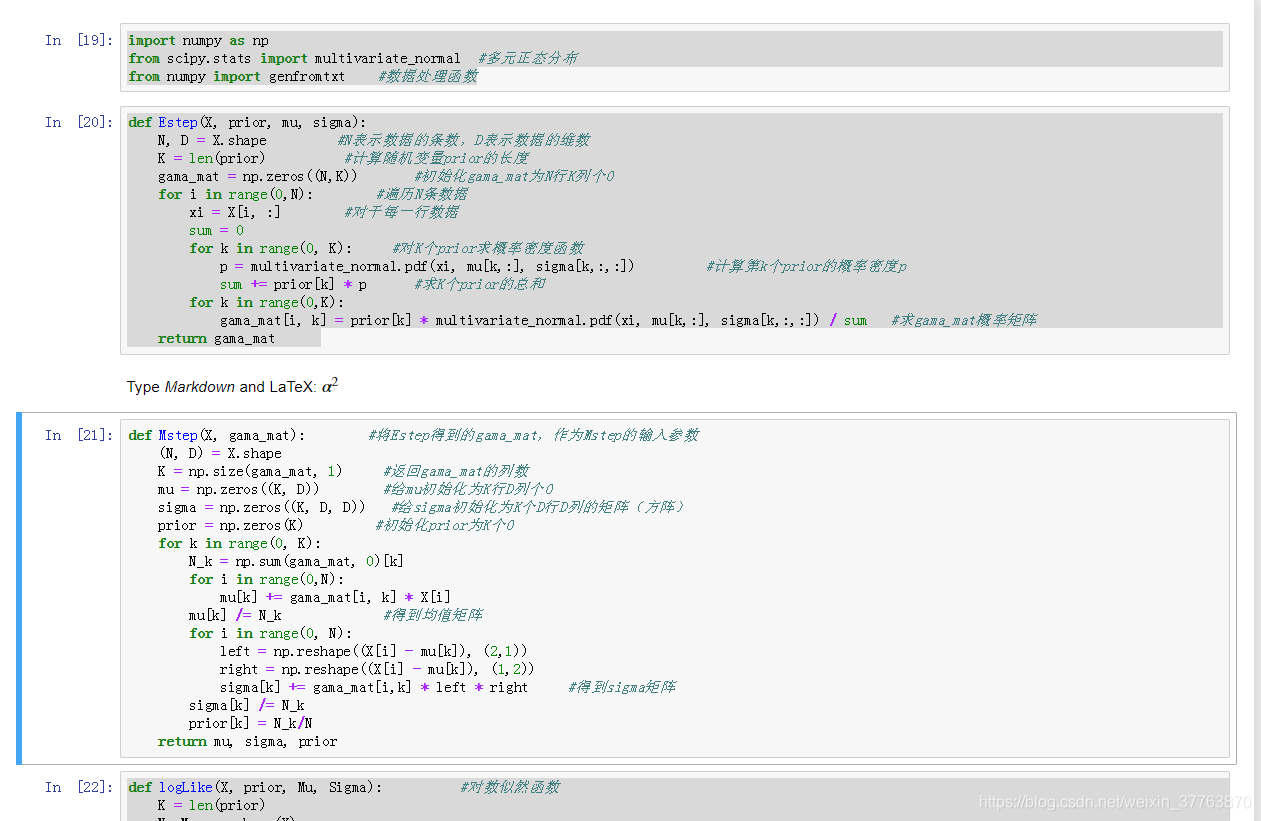
def Estep(X, prior, mu, sigma):
    N, D = X.shape         #N表示数据的条数，D表示数据的维数
    K = len(prior)          #计算随机变量prior的长度
    gama_mat = np.zeros((N,K))       #初始化gama_mat为N行K列个0
    for i in range(0,N):        #遍历N条数据
        xi = X[i, :]        #对于每一行数据
        sum = 0
        for k in range(0, K):     #对K个prior求概率密度函数
            p = multivariate_normal.pdf(xi, mu[k,:], sigma[k,:,:])         #计算第k个prior的概率密度p
            sum += prior[k] * p      #求K个prior的总和
        for k in range(0,K):
            gama_mat[i, k] = prior[k] * multivariate_normal.pdf(xi, mu[k,:], sigma[k,:,:]) / sum   #求gama_mat概率矩阵
    return gama_mat   
       
def Mstep(X, gama_mat):        #将Estep得到的gama_mat，作为Mstep的输入参数
    (N, D) = X.shape
    K = np.size(gama_mat, 1)     #返回gama_mat的列数
    mu = np.zeros((K, D))        #给mu初始化为K行D列个0 
    sigma = np.zeros((K, D, D))   #给sigma初始化为K个D行D列的矩阵（方阵）
    prior = np.zeros(K)         #初始化prior为K个0
    for k in range(0, K):
        N_k = np.sum(gama_mat, 0)[k]    
        for i in range(0,N):
            mu[k] += gama_mat[i, k] * X[i]         
        mu[k] /= N_k             #得到均值矩阵
        for i in range(0, N):
            left = np.reshape((X[i] - mu[k]), (2,1))
            right = np.reshape((X[i] - mu[k]), (1,2))
            sigma[k] += gama_mat[i,k] * left * right     #得到sigma矩阵
        sigma[k] /= N_k
        prior[k] = N_k/N
    return mu, sigma, prior
    
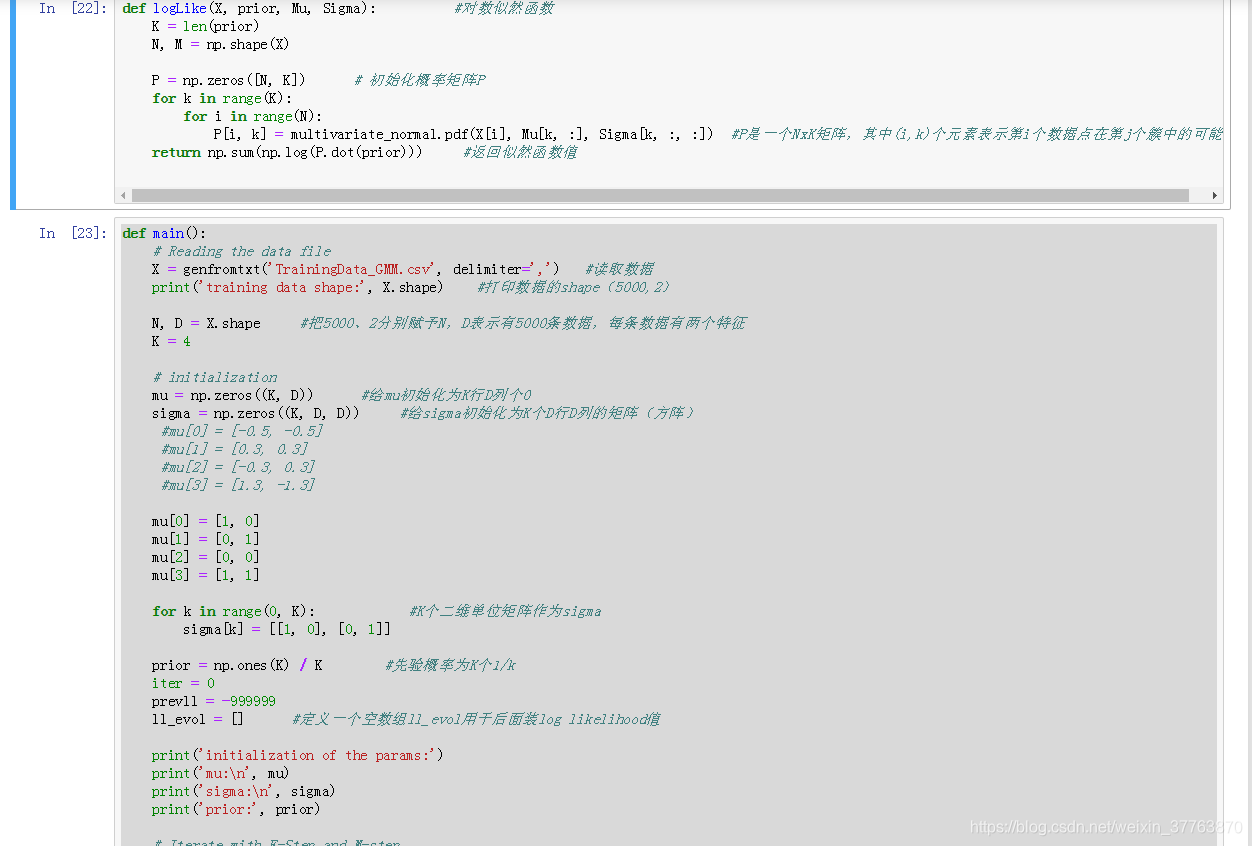
def logLike(X, prior, Mu, Sigma):          #对数似然函数
    K = len(prior)                         
    N, M = np.shape(X)
    
    P = np.zeros([N, K])      # 初始化概率矩阵P
    for k in range(K):
        for i in range(N):
            P[i, k] = multivariate_normal.pdf(X[i], Mu[k, :], Sigma[k, :, :])  #P是一个NxK矩阵，其中(i,k)个元素表示第i个数据点在第j个簇中的可能性
    return np.sum(np.log(P.dot(prior)))     #返回似然函数值
    
def main():
    # Reading the data file
    X = genfromtxt('TrainingData_GMM.csv', delimiter=',')   #读取数据
    print('training data shape:', X.shape)    #打印数据的shape（5000,2）

    N, D = X.shape     #把5000、2分别赋予N，D表示有5000条数据，每条数据有两个特征
    K = 4       

    # initialization
    mu = np.zeros((K, D))      #给mu初始化为K行D列个0
    sigma = np.zeros((K, D, D))     #给sigma初始化为K个D行D列的矩阵（方阵）
     #mu[0] = [-0.5, -0.5]
     #mu[1] = [0.3, 0.3]
     #mu[2] = [-0.3, 0.3]
     #mu[3] = [1.3, -1.3]

    mu[0] = [1, 0]
    mu[1] = [0, 1]
    mu[2] = [0, 0]
    mu[3] = [1, 1]

    for k in range(0, K):            #K个二维单位矩阵作为sigma
        sigma[k] = [[1, 0], [0, 1]]

    prior = np.ones(K) / K        #先验概率为K个1/k
    iter = 0
    prevll = -999999
    ll_evol = []      #定义一个空数组ll_evol用于后面装log likelihood值

    print('initialization of the params:')
    print('mu:\n', mu)
    print('sigma:\n', sigma)
    print('prior:', prior)

    # Iterate with E-Step and M-step
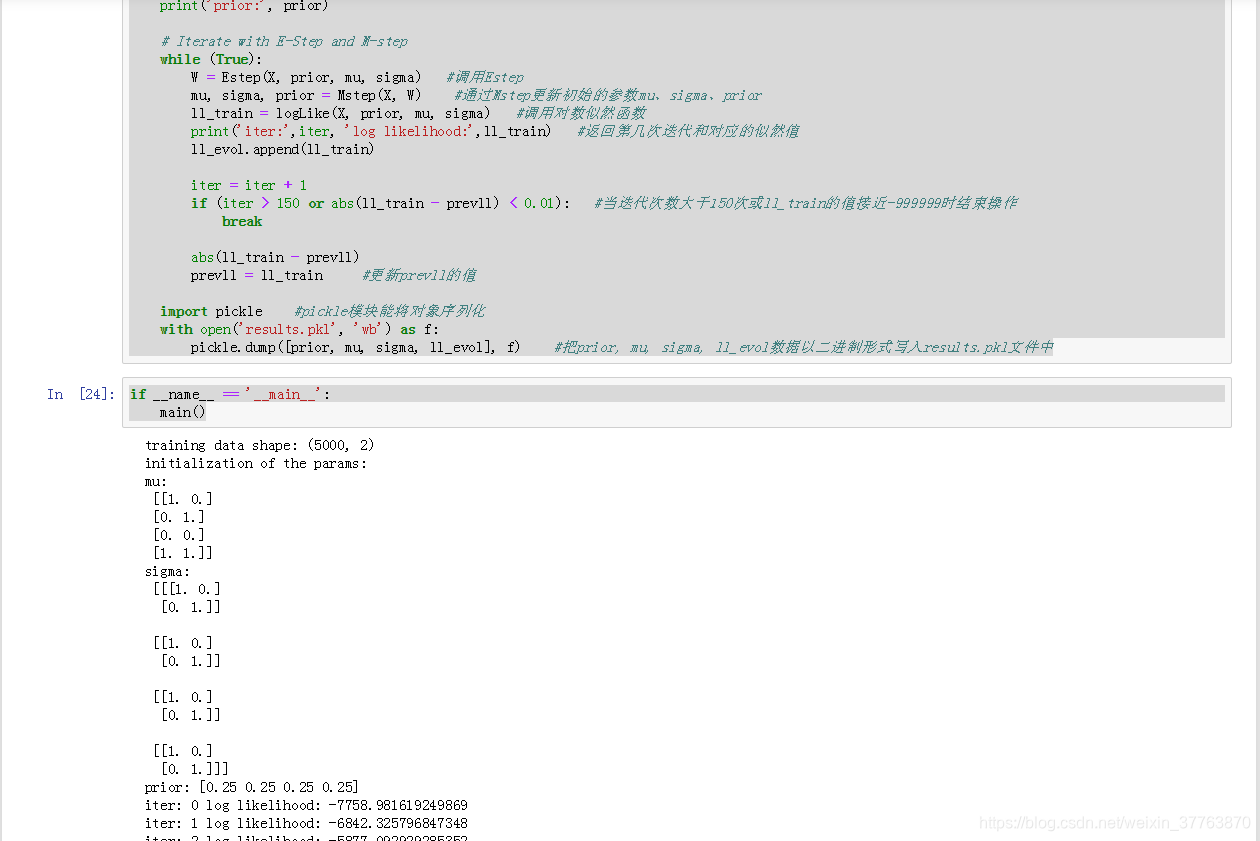
    while (True):
        W = Estep(X, prior, mu, sigma)   #调用Estep
        mu, sigma, prior = Mstep(X, W)    #通过Mstep更新初始的参数mu、sigma、prior
        ll_train = logLike(X, prior, mu, sigma)   #调用对数似然函数
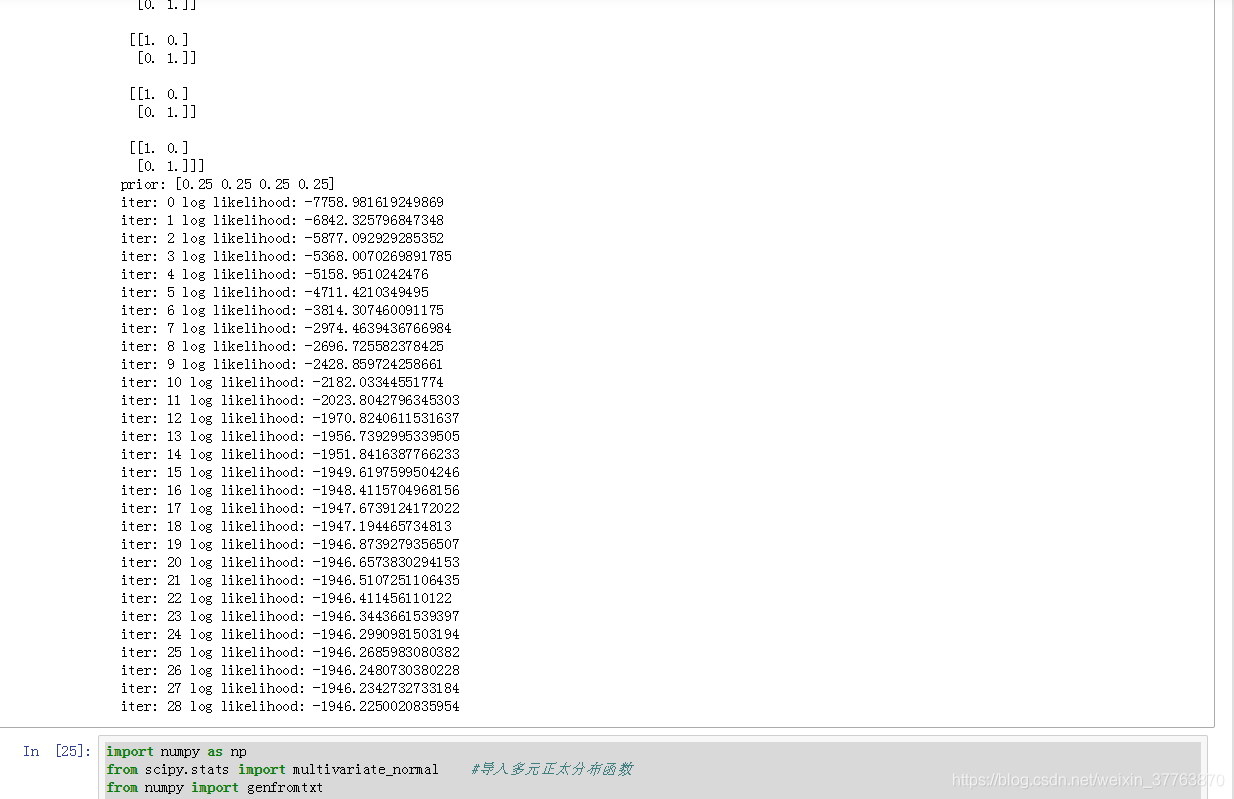
        print('iter:',iter, 'log likelihood:',ll_train)   #返回第几次迭代和对应的似然值
        ll_evol.append(ll_train)

        iter = iter + 1
        if (iter > 150 or abs(ll_train - prevll) < 0.01):   #当迭代次数大于150次或ll_train的值接近-999999时结束操作
            break

        abs(ll_train - prevll)   
        prevll = ll_train     #更新prevll的值
  
    import pickle    #pickle模块能将对象序列化
    with open('results.pkl', 'wb') as f:     
        pickle.dump([prior, mu, sigma, ll_evol], f)    #把prior, mu, sigma, ll_evol数据以二进制形式写入results.pkl文件中   
        
if __name__ == '__main__':
    main()
    
import numpy as np
from scipy.stats import multivariate_normal    #导入多元正太分布函数
from numpy import genfromtxt  
import matplotlib.pyplot as pyplot
import pickle 
with open('results.pkl', 'rb') as f:
    [prior, mu, sigma, ll_evol] = pickle.load(f)   #反序列化对象，将文件中的数据解析为python对象

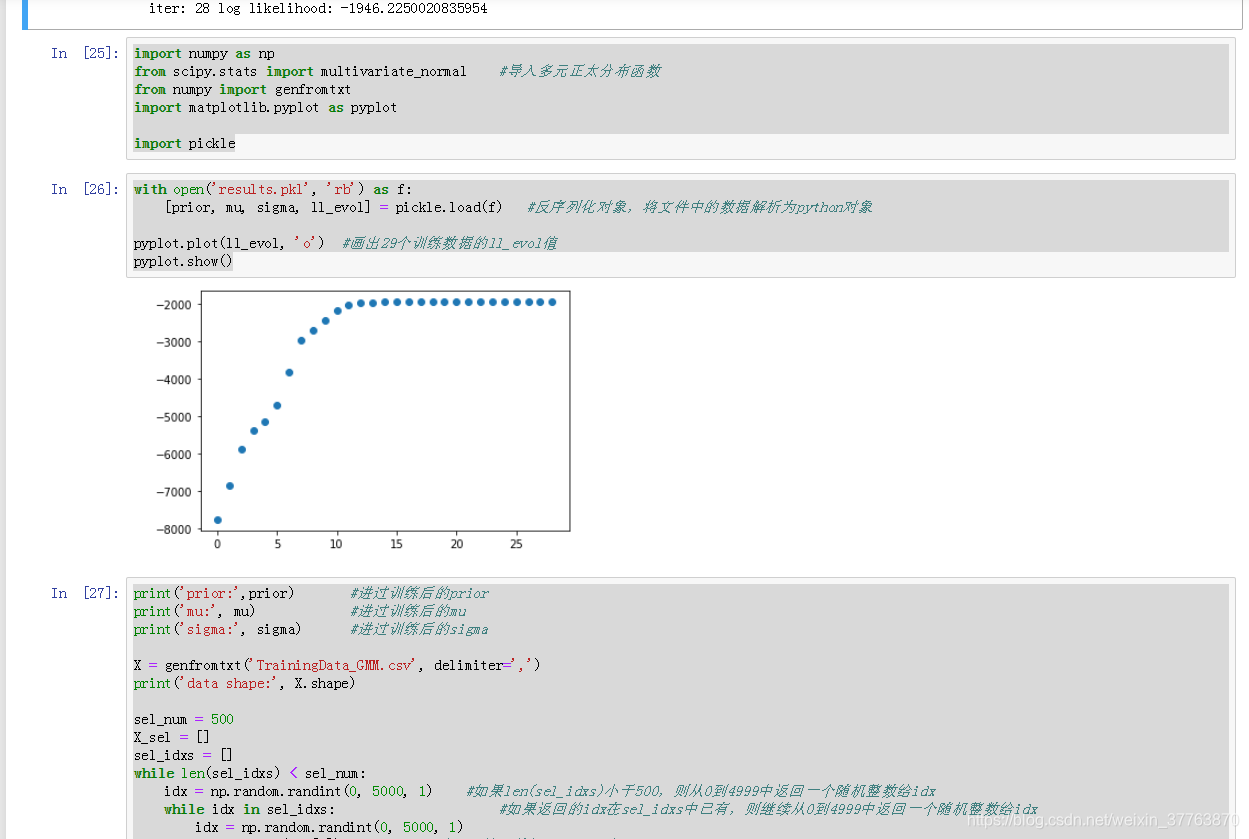
pyplot.plot(ll_evol, 'o')  #画出29个训练数据的ll_evol值
pyplot.show() 

print('prior:',prior)       #进过训练后的prior
print('mu:', mu)            #进过训练后的mu
print('sigma:', sigma)      #进过训练后的sigma

X = genfromtxt('TrainingData_GMM.csv', delimiter=',')
print('data shape:', X.shape)

sel_num = 500
X_sel = []
sel_idxs = []
while len(sel_idxs) < sel_num:
    idx = np.random.randint(0, 5000, 1)    #如果len(sel_idxs)小于500，则从0到4999中返回一个随机整数给idx
    while idx in sel_idxs:                     #如果返回的idx在sel_idxs中已有，则继续从0到4999中返回一个随机整数给idx
        idx = np.random.randint(0, 5000, 1)
    sel_idxs.append(idx[0])            #把idx放入数组sel_idxs中
X_sel = X[sel_idxs]  

def get_label(x, prior, mu, sigma):
    K = len(prior)
    p = np.zeros(K)
    for k in range(0,K):
        p[k] = prior[k] * multivariate_normal.pdf(x, mu[k,:], sigma[k,:,:])     #求k的概率p
    label = np.argmax(p)      #输出最大p对应的索引值（即label）
    return label

lbs = []
for i in range(0, sel_num):
    lb = get_label(X_sel[i], prior, mu, sigma)      #调用get_label函数传参后，得到相应的分类标签
    lbs.append(lb)

# plot
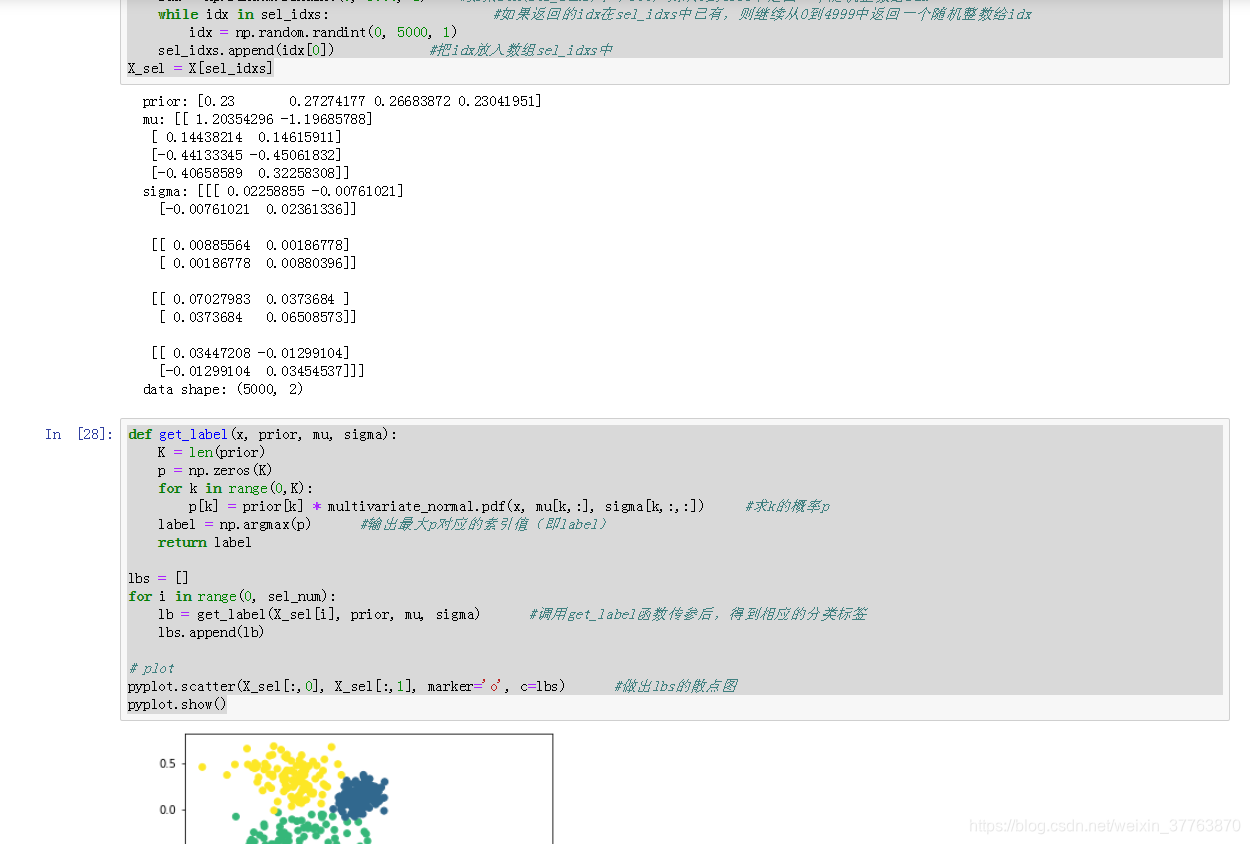
pyplot.scatter(X_sel[:,0], X_sel[:,1], marker='o', c=lbs)      #做出lbs的散点图
pyplot.show()

效果：






【附】训练数据链接
提取码：bds2