目录
一、前言:
- 吴恩达第七章Logistic回归(本文例子均来自吴恩达视频课)
- 本文公式中的θ与x均为向量而不是单个值
二、假设陈述
案例概述:根据肿瘤的大小判断是否为良性肿瘤。这是一个二项分布的问题,输出的结果分别用1和0来表示
在Logistic回归中,希望输出得是[0,1]这个范围,即为某种情况得概率(如下面这个公式就是y=1的概率)
g(z)为sigmoid函数
当得到的h_θ(x)>=0.5时,y=1
当得到的h_θ(x) < 0.5时,y=0

三、决策界限
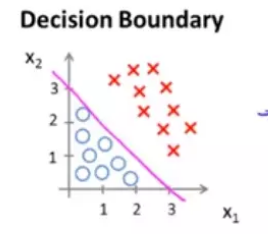
假设有以下一个数据集,拟合函数为 ,通过计算我们得到理想的参数为[-3,1,1]。
根据上一段sigmoid函数的图像可以看出
即
时 ,
通过简单的移向得到,可以在坐标系中画出以下一条直线,这条直线就称之为决策边界。
这样我们就把数据集划分为两个部分,决策边界的下面为良性肿瘤,而决策边界上面为非良性肿瘤。
对于不同的数据集分布,可以采取不同的公式进行划分。
如下图便采用圆形图像进行划分。

四、获取参数
1.CostFunction
在回归问题中,采用的代价函数如下:
但是在Logistic回归问题中不能采取相同的代价函数,因为我们采用的sigmoid函数,这使得代价函数的公式为一个非凹函数,该函数有多个较小值量,很难得到最小值。

因此在此采取新的代价函数
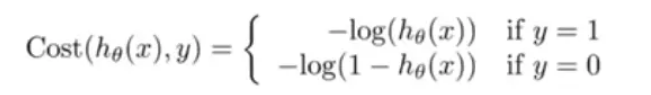
但是由于这是个分段函数,在计算过程中太麻烦,可以将此函数进行如下优化
2.梯度下降
在此梯度下降的方法与前面的线性回归的梯度下降的方式是一样的。在此直接给出公式
repeat until convergence{
(simultaneously update all )
}
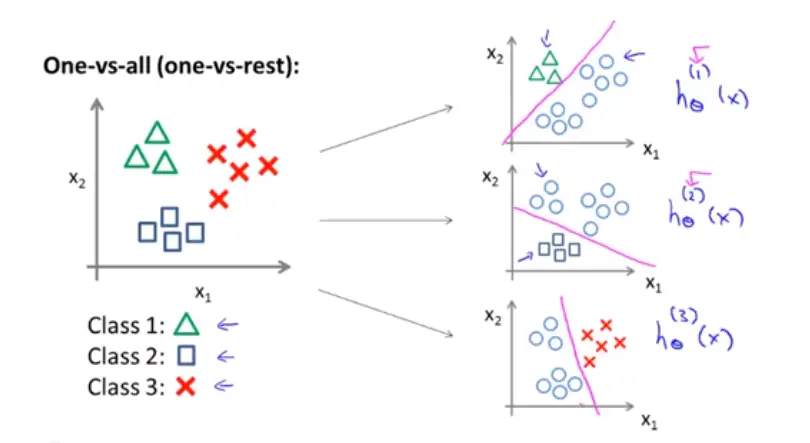
五、多元分类
前面讨论的都是两种结果的情况,只需要分出两种类别。但是现实生活中我们需要分的情况远远不止两种情况。这个时候我们只需要把一个类别单独划分出来,剩下的几种情况归为统称为另一个类别,这样就转化为一个二元分类。这样用多个函数来把给种类别划分出来