隐马尔可夫!
- 将随机变量作为结点,若两个随机变量相关或者不独立,则将二者连接一条边;若给定若干随机变量,则形成一个有向图,即构成一个网络
- 如果该网络是有向无环图,则这个网络称为贝叶斯网络。
- 如果这个图退化成线性链的方式,则得到马尔可夫模型;因为每个结点都是随机变量,将其看成各个时刻(或空间)的相关变化,以随机过程的视角,则可以看成是马尔可夫过程。
- 若上述网络是无向的,则是无向图模型,又称马尔可夫随机场或者马尔可夫网络。
- 如果在给定某些条件的前提下,研究这个马尔可夫随机场,则得到条件随机场。
- 如果使用条件随机场解决标注问题,并且进一步将条件随机场中的网络拓扑变成线性的,则得到线性链条件随机场。
马尔可夫性质
- 设
X(t),t∈T是一个随机过程,E为其状态空间,若对于任意的
t1<t2<...<tn<t,任意的
x1,x2,...,xn,x∈E,随机变量X(t)在已知变量
X(t1)=x1,...,X(tn)=xn之下的条件分布函数只与
X(tn)=xn有关,而与
X(t1)=x1,...,X(tn−1)=xn−1无关,即条件分布函数满足下列等式,此性质称为马尔可夫性;
如果随机过程满足马尔可夫性,则该过程称为马尔可夫过程。
p(X(t)≤x∣X(x1)=x1,...,xX(tn)=xn)=p(X(t)≤x∣X(tn)=xn)
p(Xn+1=x∣X1=x1,...,Xn=xn)=p(Xn+1∣Xn=xn)
马尔可夫链
- 马尔可夫链是指具有马尔可夫性质的随机过程。在过程中,在给定当前信息的情况下,过去的信息状态对于预测将来状态是无关的。
- 在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变成另外一个状态,也可以保持当前状态不变。状态的改变叫做转移,状态改变的相关概率叫做转移概率。
- 马尔可夫链中的三元素是:状态空间S、转移概率矩阵P、初始概率分布π。
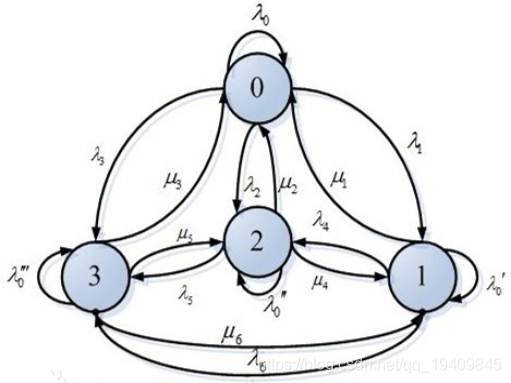
马尔可夫链案例
-
设将天气状态分为晴、阴、雨三种状态,假定某天的天气状态只和上一天的天气状态有关,状态使用1(晴)、2(阴)、3(雨)表示,转移概率矩阵P如下:
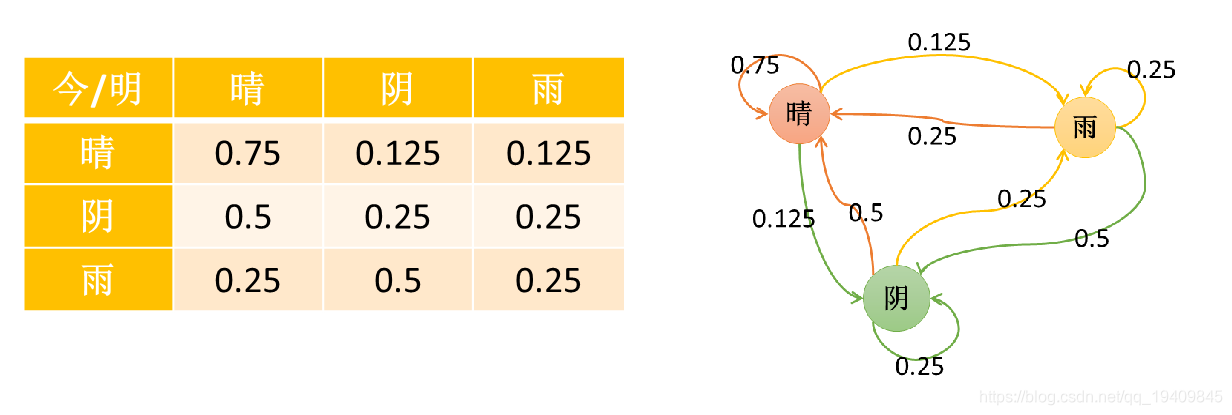
-
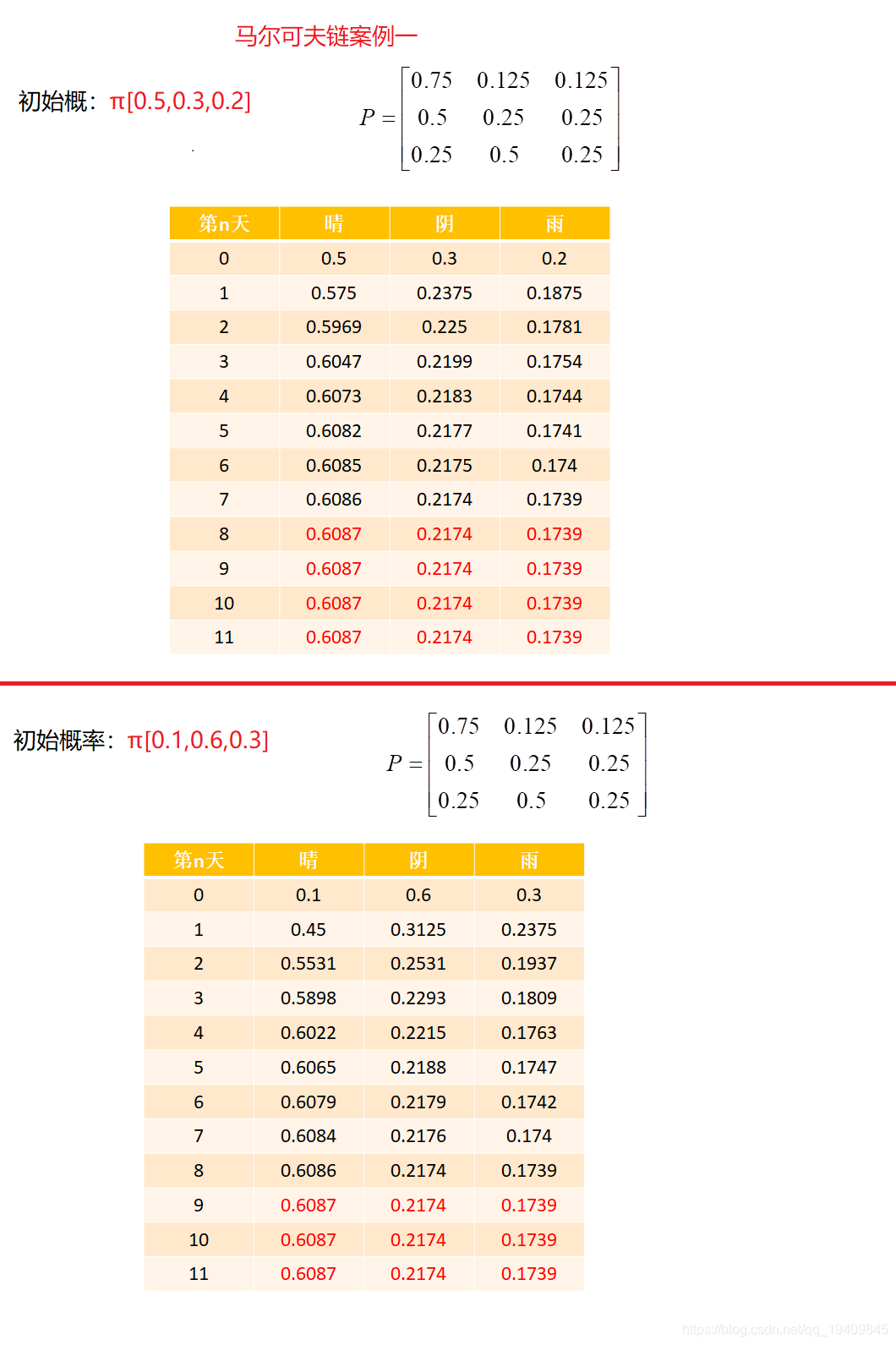
第n+1天天气状态为j的概率为:
π(Xn+1=j)=i=1∑Kπ(Xn=i)⋅P(Xn+1=j∣Xn=i)⇒πn+1=πn⋅P
-
因此,矩阵P即为条件概率转移矩阵。
- 矩阵P的第i行元素表示,在上一个状态为i的时候的分布概率,即每行元素的和必须为1
隐马尔可夫模型HMM
-
隐马尔可夫模型(Hidden Markov Model, HMM)是一种统计模型,在语音识别、行为识别、NLP、故障诊断等领域具有高效的性能。
-
HMM是关于时序的概率模型,描述一个含有未知参数的马尔可夫链所生成的不可观测的状态随机序列,再由各个状态生成观测随机序列的过程。HMM是一个双重随机过程—具有一定状态的隐马尔可夫链和随机的观测序列。
-
HMM随机生成的状态随机序列被称为状态序列;每个状态生成一个观测,由此产生的观测随机序列,被称为观测序列。
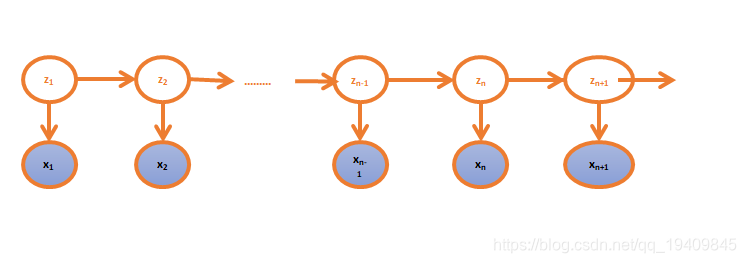
-
上图中
z1,z2...,zn是不可观测的状态,
x1,x2,...xn是可观测到的序列;不可观测的状态决定可观测序列的值(z的取值决定x的取值)。
-
HMM由隐含状态S、可观测状态O、初始状态概率矩阵/向量π、隐含状态转移概率矩阵A、可观测值转移矩阵B(又称为混淆矩阵,Confusion Matrix);
-
π和A决定了状态序列,B决定观测序列,因此HMM可以使用三元符号表示,称为HMM的三元素:
λ=(A,B,π)
HMM参数说明
- S是所有可能的状态集合:
S={s1,s2,...,sn}
- O是所有可能的观测集合:
O={o1,o2,...,om}
- I是长度为T的状态序列,Q是对应的观测序列
I={i1,i2,...,iT}
Q={q1,w2,...,qT}
A是隐含状态转移概率矩阵:
A=[aij]n∗n=⎣⎢⎢⎢⎡a11a21⋮an1a12a22⋮a2⋯⋯⋮⋯a1na2n⋮ann⎦⎥⎥⎥⎤
- 其中
-
aij是在时刻t处于状态
si的条件下时刻t+1转移到状态
sj的概率。
aij=p(it+1=s∣i=si)
B是可观测值转移概率矩阵:
B=[bij]n∗m=⎣⎢⎢⎢⎡b11b21⋮bn1b12b22⋮b2⋯⋯⋮⋯b1mb2m⋮bnm⎦⎥⎥⎥⎤
- 其中
-
bij是在时刻t处于状态
si的条件下生成观测值
oj的概率。
bij=p(qt=oj∣it=st)
π是初始状态概率向量:
π=(πi)1∗n=(π1,π2,...,πn)
其中
πi是在时刻t=1处于状态si的概率。
πi=p(i1=si)
HMM的两个基本性质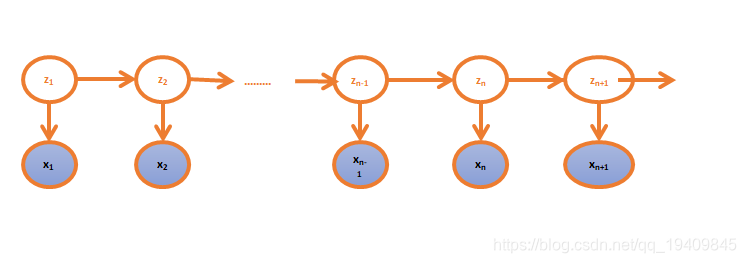
- 性质一:
p(it∣it−1,qt−1,it−2,qt−2,...,i1,q1)=p(it∣it−1)
- 性质二:
p(qt∣it,it−1,qt−1,it−2,qt−2,...,i1,q1)=p(qt∣it)
HMM的三个问题
概率计算问题:前向-后向算法
- 给定模型λ=(A,B,π),计算模型λ下观测到序列Q={
q1,q2,...,qT}出现的概率P(Q|λ)
直接计算
- 按照概率公式,列举所有可能的长度为T的状态序列I={
i1,i2,...,iT},求各个状态序列I与观测序列Q={
q1,q2,...,qT}的联合概率P(Q,I;λ),然后对所有可能的状态序列求和,从而得到最终的概率P(Q;λ)
I={i1,i2,...,iT}p(I;λ)=πi1ai1i2ai2i3....aiT−1iT
Q={q1,q2,...,qT}p(Q∣I;λ)=bi1q1bi2q2....biTqT
P(Q,I;λ)=p(Q∣I;λ)p(I;λ)=πi1ai1i2ai2i3....aiT−1iTbi1q1bi2q2....biTqT
p(Q;λ)=I∑p(Q,I;λ)=i1,i2,..,iT∑πi1ai1i2ai2i3....aiT−1iTbi1q1bi2q2....biTqT
前向概率-后向概率
- 前向概率-后向概率指的其实是在一个观测序列中,时刻t对应的状态为si,并且观测序列已知情况下的联合概率值转换过来的值。
p(q1,q2....qT,it=si)
=p(q1,q2....qt,it=si)p(qt+1,qt+2....qT,∣q1,q2....qt,it=si)=p(q1,q2....qt,it=si)p(qt+1,qt+2....qT,∣it=si)=αt(i)∗βt(i)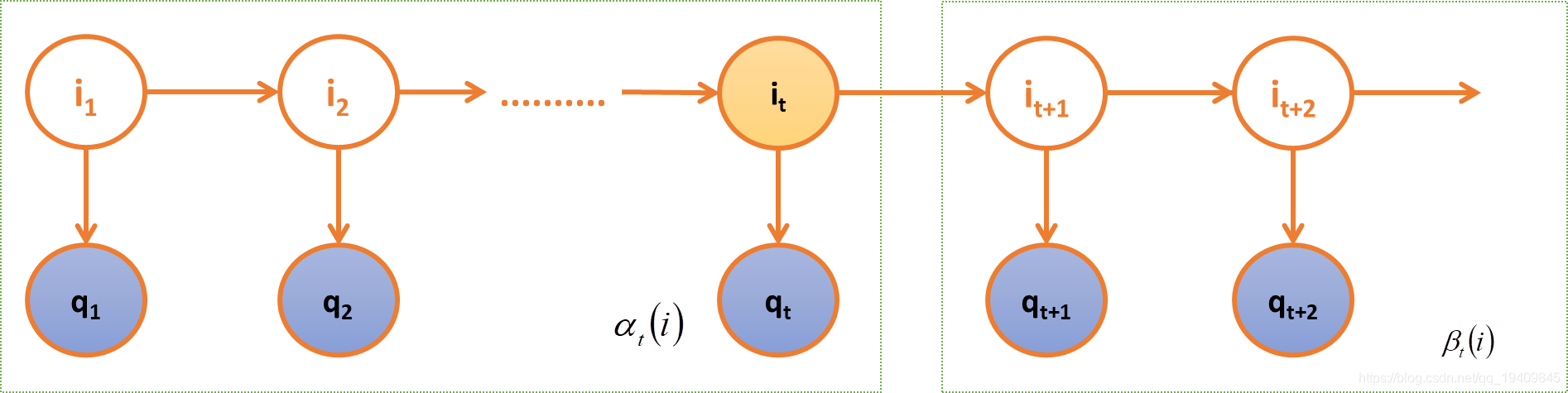
αt(i)=p(q1,q2....qt,it=si)
βt(i)=p(qt+1,qt+2....qT∣it=si)
向前算法:
-
定义:给定λ,定义到时刻t部分观测序列为
q1,q2,...,qt且状态为
si的概率为前向概率。记做:
αt(i)=p(q1,q2,...,qt,it=si;λ)=p(q1,q2,...,qt−1,it=si)∗p(qt∣q1,q2,...,qt−1,it=si)=p(q1,q2,...,qt−1,it=si)∗p(qt∣it=si)=[j=1∑np(q1,q2,...,qt−1,it−1=sj,it=si)]∗p(qt∣it=si)=[j=1∑np(q1,q2,...,qt−1,it−1=sj)p(it=si∣it−1=sj)]∗p(qt∣it=si)=(j=1∑nαt−1(j)aji)biqt
-
初值:
α1(i)=p(q1,i1=si;λ)=πibiq1
-
递推:对于t=1,2,…,T-1
αt+1(i)=(j=1∑nαt(j)aji)biqt+1
-
最终:
P(Q;λ)=i=1∑nαT(i)βT(i)=i=1∑nαT(i)
后向算法
- 定义:给定λ,定义到时刻t状态为si的前提下,从t+1到T部分观测序列为qt+1,qt+2,…,qT的概率为后向概率。记做:
βt(i)=p(qt+1,qt+2,...,qT∣it=si;λ)
βt(i)=p(qt+1,qt+2,...,qT∣it=si)=j=1∑np(it+1=sj,qt+1,qt+2,...,qT∣it=si)=j=1∑np(qt+1,qt+2,...,qT∣it+1=sj)p(it+1=sj∣it=si)=j=1∑np(qt+2,...,qT∣it+1=sj)p(qt+1∣it+1=sj)p(it+1=sj∣it=si)=j=1∑n(aijbjqt+1βt+1(j))
-
初值:
βT(i)=1
-
递推:对于t=T-1,T-2,…,1
βt(i)=j=1∑n(aijbjqt+1βt+1(j))
-
最终:
P(Q;λ)=i=1∑nα1(i)β1(i)=i=1∑nπibiq1β1(i)
单个状态的概率
-
求给定模型λ和观测序列Q的情况下,在时刻t处于状态si的概率,记做:
γt(i)=p(it=si∣Q;λ)
-
单个状态概率的意义主要是用于判断在每个时刻最可能存在的状态,从而可以得到一个状态序列作为最终的预测结果。
p(it=si,Q;λ)=αt(i)βt(i)
γt(i)=p(it=si∣Q;λ)=p(Q;λ)p(it=si,Q;λ)
γt(i)=P(Q;λ)αt(i)βt(i)=j=1∑nαt(j)βt(j)αt(i)βt(i)
两个状态的联合概率
- 求给定模型λ和观测序列Q的情况下,在时刻t处于状态
si并时刻t+1处于状态
sj概率,记做:
ξt(i,j)=p(it=si,it+1=sj∣Q;λ)=p(Q;λ)p(it=si,it+1=sj,Q;λ)=i=1∑nj=1∑np(it=si,it+1=sj,Q;λ)p(it=si,it+1=sj,Q;λ)
p(it=si,it+1=sj,Q;λ)=αt(i)aijbjqt+1βt+1(j)
学习问题:Baum-Welch算法(状态未知)
- 已知观测序列Q={
q1,q2,...,qT},估计模型λ=(A,B,π)的参数,使得在该模型下观测序列P(Q|λ)最大。
- 若训练数据包含观测序列和状态序列,则HMM的学习问题非常简单,是监督学习算法。
- 若训练数据只包含观测序列,则HMM的学习问题需要使用EM算法求解,是无监督学习算法。
Baum-Welch算法
A求解:
- 极大化L,使用拉格朗日乘子法,求解
aij的值:
I∑(t=1∑T−1lnaitit+1)p(I,Q;λˉ)=i=1∑nj=1∑nt=1∑T−1lnaijp(Q,it=i,it+1=j;λˉ)
i=1∑nj=1∑nt=1∑T−1lnaijp(Q,it=i,it+1=j;λˉ)+β(i=1∑nj=1∑naij−n)
t=1∑T−1p(Q,it=i,it+1=j;λˉ)+βaij=0
aij=t=1∑T−1p(Q,it=i;λˉ)t=1∑T−1p(Q,it=i,it+1=j;λˉ)=t=1∑T−1γt(i)t=1∑T−1ξt(i,j)
B求解
-
极大化L,使用拉格朗日乘子法,求解
bij的值:
I∑(t=1∑Tlnbitqt)p(I,Q;λˉ)=i=1∑nj=1∑mt=1∑Tlnbijp(Q,it=i,qt=j;λˉ)
i=1∑nj=1∑mt=1∑Tlnbijp(Q,it=i,qt=j;λˉ)+β(i=1∑nj=1∑nbij−n)
t=1∑Tp(Q,it=i,qt=j;λˉ)+βbij=0
bij=t=1∑Tp(Q,it=i;λˉ)t=1∑Tp(Q,it=i,qt=j;λˉ)=t=1∑Tp(Q,it=i;λˉ)t=1,qt=j∑Tp(Q,it=i;λˉ)=t=1∑Tγt(i)t=1,qt=j∑Tγt(i)
-
极大化L函数,分别可以求得π、a、b的值。
πi=γ1(i)
aij=t=1∑T−1γt(i)t=1∑T−1ξt(i,j)
bij=t=1∑Tγt(i)t=1,qt=oj∑Tγt(i)
预测问题:Viterbi算法
- 给定模型λ=(A,B,π)和观测序列Q={
q1,q2,...,qT},求给定观测序列条件概率P(I|Q,λ)最大的状态序列I
近似算法
- 直接在每个时刻t时候最优可能的状态作为最终的预测状态,使用下列公式计算概率值:
γt(i)=P(Q;λ)αt(i)βt(i)=j=1∑nαt(j)βt(j)αt(i)βt(i)
Viterbi算法
- Viterbi算法实际是用动态规划的思路求解HMM预测问题,求出概率最大的“路径”,每条“路径”对应一个状态序列。
δt(i)=i1,i2,..,it−1maxp(it=i,i1,i2,..,it−1,qt,qt−1,..,q1;λ)
δt+1(i)=1⩽j⩽nmax(δt(j)aji)biqt+1
P∗=1⩽i⩽nmaxδT(i)
HMM案例-Viterbi
- 在给定参数π、A、B的时候,得到观测序列为“白黑白白黑”,求出最优的隐藏状态序列。
π=⎝⎛0.20.50.3⎠⎞A=⎣⎡0.50.20.20.40.20.50.10.60.3⎦⎤B=⎣⎡0.40.80.50.60.20.5⎦⎤
δ1(i)=πibiq1=πibi白
δ1(1)δ1(2)δ1(3)=0.08=0.4=0.15
δ2(i)=1⩽j⩽3max(δ1(j)aji)biq2=1⩽j⩽3max(δ1(j)aji)bi黑
δ2(1)δ2(2)δ2(3)=max{0.08∗0.5,0.4∗0.2,0.15∗0.2}∗0.6=0.048=max{0.08∗0.4,0.4∗0.2,0.15∗0.5}∗0.2=0.01=max{0.08∗0.1,0.4∗0.6,0.15∗0.3}∗0.5=0.12
δ2(1)δ2(2)δ2(3)=0.048=0.016=0.12
δ3(i)=1⩽j⩽3max(δ2(j)aji)biq3=1⩽j⩽3max(δ2(j)aji)bi白
δ3(1)=max{0.048∗0.5,0.016∗0.2,0.12∗0.2}∗0.4δ3(2)=max{0.048∗0.4,0.016∗0.2,0.12∗0.5}∗0.8δ3(3)=max{0.048∗0.1,0.016∗0.6,0.12∗0.3}∗0.5=0.024∗0.4=0.0096=0.06∗0.8=0.048=0.036∗0.5=0.018
δ3(1)δ3(1)δ3(3)=0.0096=0.0096=0.018
δ4(i)=1⩽j⩽3max(δ3(j)aji)biq4=1⩽j⩽3max(δ3(j)aji)bi白
δ4(1)δ4(2)δ4(3)=max{0.0096∗0.5,0.048∗0.2,0.018∗0.2}∗0.4=0.0096∗0.4=0.0096=max{0.0096∗0.4,0.048∗0.2,0.018∗0.5}∗0.8=0.0096∗0.8=0.00768=max{0.0096∗0.1,0.048∗0.6,0.018∗0.3}∗0.5=0.0288∗0.5=0.0144
δ4(1)δ4(2)δ4(3)=0.00384=0.00768=0.0144
δ5(i)=1⩽j⩽3max(δ4(j)aji)biq5=1⩽j⩽3max(δ4(j)aji)bi黑
δ5(1)=max{0.00384∗0.5,0.00768∗0.2,0.0144∗0.2}∗0.6δ5(2)=max{0.00384∗0.4,0.00768∗0.2,0.0144∗0.5}∗0.2δ5(3)=max{0.00384∗0.1,0.00768∗0.6,0.0144∗0.3}∗0.5=0.00288∗0.6=0.001728=0.0072∗0.2=0.00144=0.004608∗0.5=0.002304
最终盒子序列为:(2,3,2,2,3)(选择概率最大的)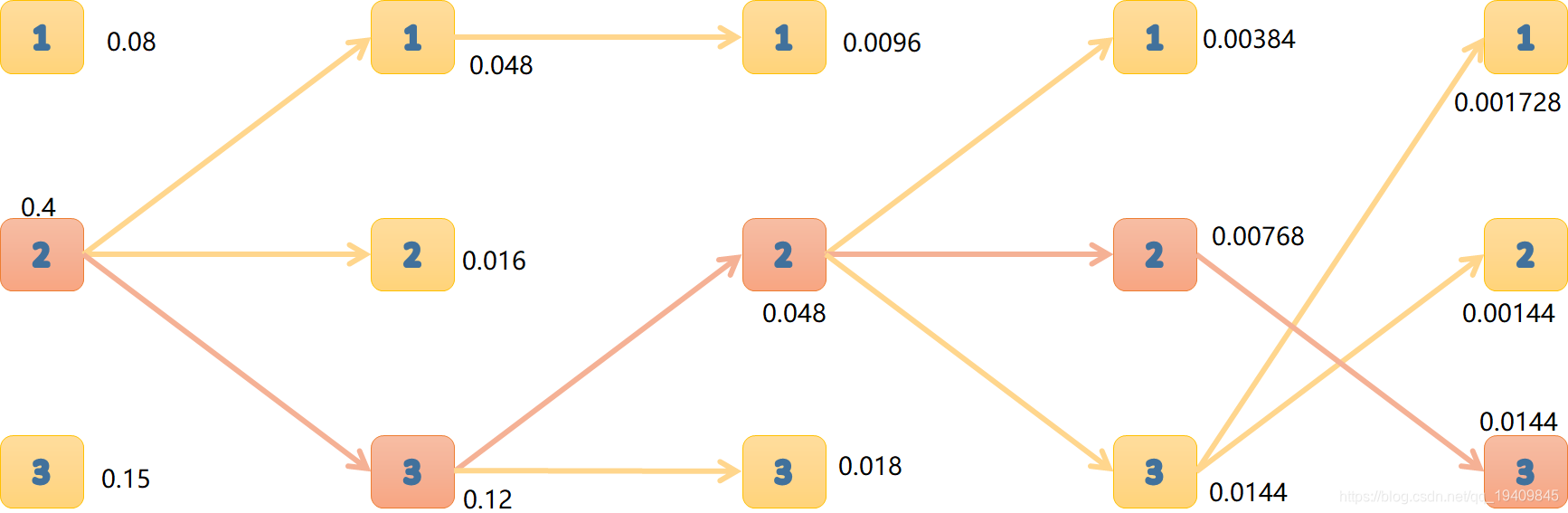
条件随机场(CRF)
-
假设你有许多小明同学一天内不同时段的照片,从小明提裤子起床到脱裤子睡觉各个时间段都有(小明是照片控!)。现在的任务是对这些照片进行分类。比如有的照片是吃饭,那就给它打上吃饭的标签;有的照片是跑步时拍的,那就打上跑步的标签;有的照片是开会时拍的,那就打上开会的标签。问题来了,你准备怎么干?一个简单直观的办法就是,不管这些照片之间的时间顺序,想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据,训练出一个模型,直接根据照片的特征来分类。例如,如果照片是早上6:00拍的,且画面是黑暗的,那就给它打上睡觉的标签;如果照片上有车,那就给它打上开车的标签。
-
乍一看可以!但实际上,由于我们忽略了这些照片之间的时间顺序这一重要信息,我们的分类器会有缺陷的。举个例子,假如有一张小明闭着嘴的照片,怎么分类?显然难以直接判断,需要参考闭嘴之前的照片,如果之前的照片显示小明在吃饭,那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽,可以给它打上吃饭的标签;如果之前的照片显示小明在唱歌,那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍,可以给它打上唱歌的标签。
-
所以,为了让我们的分类器能够有更好的表现,在为一张照片分类时,我们必须将与它**相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方!**这就有点类似于词性标注了,只不过把照片换成了句子而已,本质上是一样的。
-
如同马尔可夫随机场,条件随机场为具有无向的图模型,图中的顶点代表随机变量,顶点间的连线代表随机变量间的相依关系,在条件随机场中,随机变量Y 的分布为条件机率,给定的观察值则为随机变量 X。下图就是一个线性连条件随机场。
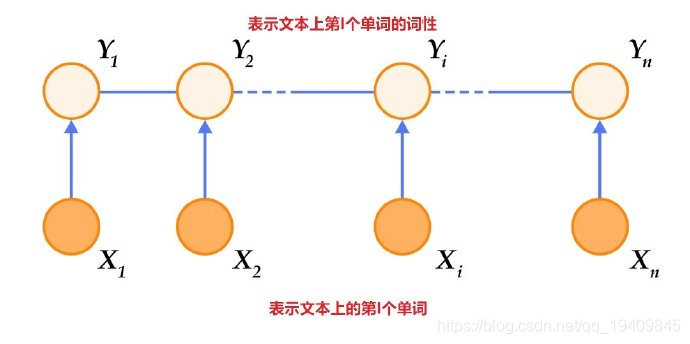
条件概率分布P(Y|X)称为条件随机场。
EM算法、HMM、CRF的比较
-
EM算法是用于含有隐变量模型的极大似然估计或者极大后验估计,有两步组成:E步,求期望(expectation);M步,求极大(maxmization)。本质上EM算法还是一个迭代算法,通过不断用上一代参数对隐变量的估计来对当前变量进行计算,直到收敛。注意:EM算法是对初值敏感的,而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法,也就是说EM算法不能保证找到全局最优值。对于EM的导出方法也应该掌握。
-
隐马尔可夫模型(HMM)是用于标注问题的生成模型。有几个参数(π,A,B):初始状态概率向量π,状态转移矩阵A,观测概率矩阵B。称为马尔科夫模型的三要素。马尔科夫三个基本问题:
-
概率计算问题:给定模型和观测序列,计算模型下观测序列输出的概率。–》前向后向算法
-
学习问题:已知观测序列,估计模型参数,即用极大似然估计来估计参数。–》Baum-Welch(也就是EM算法)和极大似然估计。
-
预测问题:已知模型和观测序列,求解对应的状态序列。–》近似算法(贪心算法)和维比特算法(动态规划求最优路径)
-
条件随机场CRF,给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场,而我们平时看到的大多是线性链条随机场,也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。
-
之所以总把HMM和CRF进行比较,主要是因为CRF和HMM都利用了图的知识,但是CRF利用的是马尔科夫随机场(无向图),而HMM的基础是贝叶斯网络(有向图)。而且CRF也有:概率计算问题、学习问题和预测问题。大致计算方法和HMM类似,只不过不需要EM算法进行学习问题。
-
HMM和CRF对比其根本还是在于基本的理念不同,一个是生成模型,一个是判别模型,这也就导致了求解方式的不同








