首先来了解拉格朗日插值法。

可理解为:
个点为(xi,yi),这个多项式可以看做n个下面的函数的和。其中,第i个多项式函数fi除了在fi(xi)=yi外,其他的位置取值都为0,即fi(xj)=0(i≠j)。
f(x)=a(x−x1)(x−x2)
显然在f(x)=0
时,必有x1,x2
两解。推而广之,一个有n个顶点的n次多项式可以写为,
f(x)=a(x−x1)(x−x2)……(x−xn)
那么插值用的第i个多项式可写作为 :![]()
又有fi(xi)=yi,带入xi,可得:

即可得:
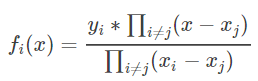
即插值公式为:
扫描二维码关注公众号,回复:
8780192 查看本文章


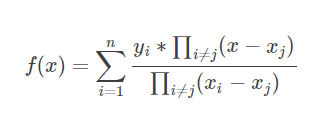
如果还不理解的话,举个栗子。
eg:比方说我们已经得到了三个带点(2,5),(3,7),(9,11)
我们利用公式:就能得出结果了。
附上一道例题,题目来源:https://nanti.jisuanke.com/t/40254
这是2019南昌邀请赛现场赛的B题。
f(x)是n次多项式,有n+1个未知数,已知n+1个方程,所以可以f(x)是确定的。从L到R的f(x)的总和。
因为题目中给定的是从0-n的f(x)的值,因为0-n都是连续的可以进行预处理来写,此公式可以化成:
fact[i]就是阶乘i!
但是分母fact[n-i]可能出现负数,需要去判断,当 n-i 为奇数时,分母应该取负号。
finv[i]是阶乘 i !的逆元,因为的阶乘分之一,这边因为mod=9999991是一个质数,求逆元。
因为时间的关系不能用暴力求解,从而可以使用到前缀和,因为是连续的,变量只有yi,用sum[i]表示前缀和来做。
由于n次多项式的前缀和是n+1次的多项式,也就是说 f(x) 要通过 n+2 个点来求出,然而题目只给出了n+1 个点,所以我们增加一个a[n+1],之后就可以进行插值了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=9999991;
ll a[1010],sum[1010],fact[1010],pre[1010],suff[1010],finv[1010];
ll quickpow(ll a,ll b)
{
ll res=1;
while(b)
{
if(b&1)
res=(res*a)%mod;
b>>=1;
a=(a*a)%mod;
}
return res%mod;
}
void init()
{
fact[0]=1;
int i,j,k;
for(i=1;i<1010;i++)
{
fact[i]=fact[i-1]*i%mod;
}
finv[1009]=quickpow(fact[1009],mod-2);
for(i=1008;i>=0;i--)
{
finv[i]=finv[i+1]*(i+1)%mod;
}
}
ll solve(ll hh[],ll n,ll x)
{
if(x<=n)
return hh[x];
int i,j,k;
pre[0]=1,suff[n]=1;
int ans=0;
for(int i=1;i<=n;i++)
pre[i]=ll(pre[i-1]*(x-(i-1)))%mod;
for(int i=n-1;i>=0;i--)
suff[i]=ll(suff[i+1]*(x-(i+1)))%mod;
for(int i=0;i<=n;i++)
{
int fuhao=(n-i)&1?-1:1;
ans+=hh[i]%mod*fuhao*pre[i]%mod*suff[i]%mod*finv[i]%mod*finv[n-i]%mod;
ans=(ans%mod+mod)%mod;
}
return ans;
}
int main()
{
init();
int T;
scanf("%d",&T);
while(T--)
{
int n,m,i,j;
scanf("%d %d",&n,&m);
for(i=0;i<=n;i++)
{
scanf("%d",&a[i]);
}
a[n+1]=solve(a,n,n+1);
sum[0]=a[0];
for(i=1;i<=n+1;i++)
{
sum[i]=(sum[i-1]+a[i])%mod;
}
while(m--)
{
int left,right;
scanf("%d %d",&left,&right);
ll ans=(solve(sum,n+1,right)-solve(sum,n+1,left-1));
ans=(ans%mod+mod)%mod;
printf("%lld\n",ans);
}
}
return 0;
} 