带电粒子在随时间缓慢变化的磁场中的运动

如果磁场随时间缓慢变化，根据法拉第定律， $\bm{\nabla}\times \bm{E}= - \partial \bm{B}/\partial t$，会产生一个非保守电场，从而粒子总能量不再守恒。

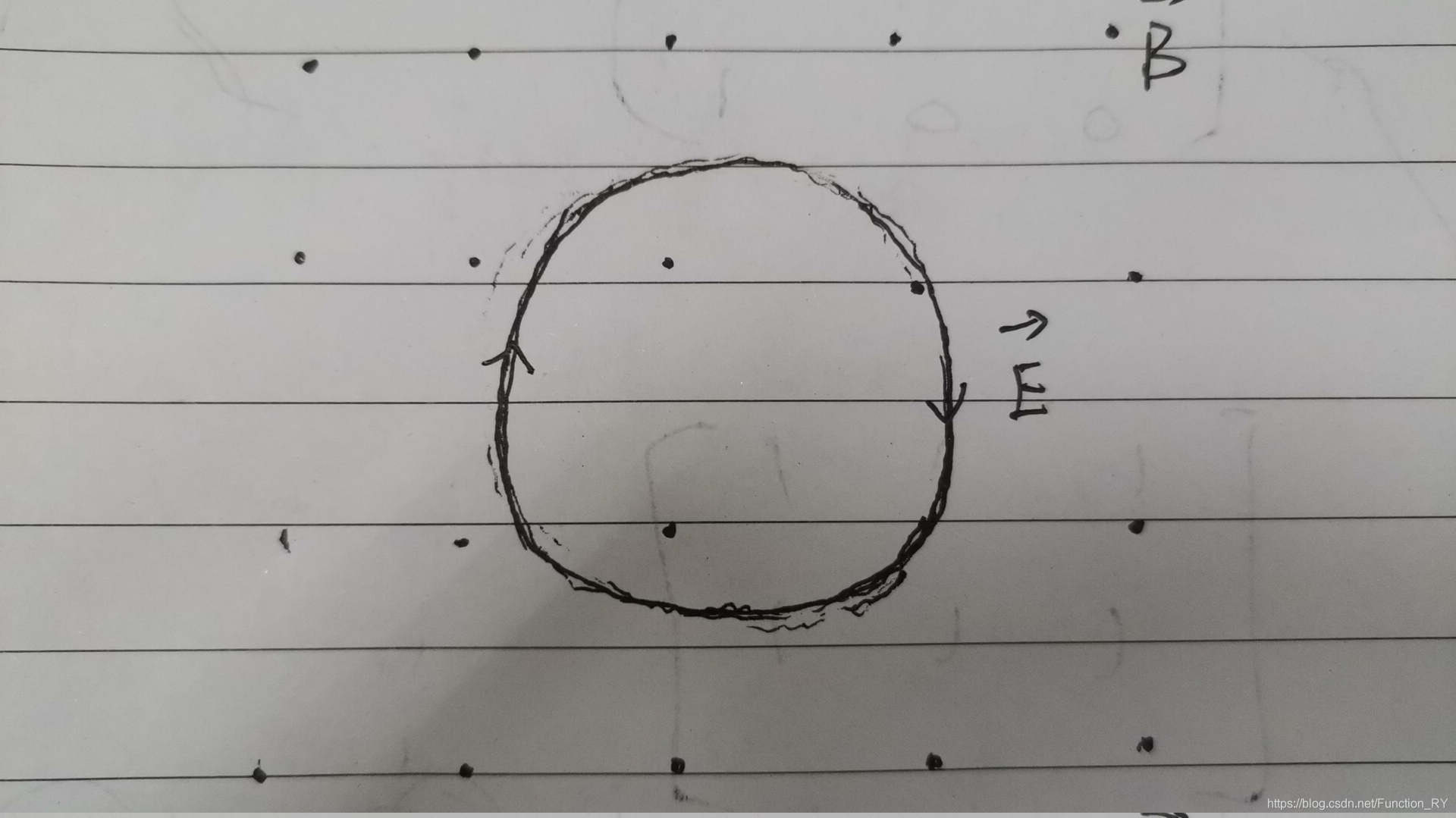
设磁场在空间分布均匀，则粒子在一个回旋周期内，动能的变化量为
$\Delta \omega _\bot = q \int_C \bm{E \cdot}d\bm{l} = - q\int_S \frac{\partial \bm{B}}{\partial t} \cdot d\bm{A}$

其中用了 斯托克斯定理 ，将线积分化为面积分。由于磁场随时间缓慢变化，粒子近似为圆周运动，圆周面积为 $\pi \rho_c^2$，则动能改变量化为
$\Delta \omega _\bot = |q| \frac{dB}{d t} \pi \rho_c^2$

使用 $|q|$是因为能量变化与电荷符号无关。粒子的回旋周期 $\Delta t = 2\pi /\omega_c$，则垂直动能的变化率为
$\frac{d\omega_\bot}{dt} = \frac{\omega_c}{2\pi} \frac{dB}{d t} (\pi \rho_c^2)$

其中 $(1/2\pi)\omega_c |q| \pi \rho_c^2$为磁矩，上式写成
$\frac{d\omega_\bot}{dt} = \mu \frac{dB}{d t}$

又 $\mu = \omega_\bot / B$，上式化为
$\frac{d\omega_\bot}{\omega} = \frac{dB}{B}$

积分可以得到
$\frac{\omega_\bot }{B}=常量$

从而得到，粒子在随时间缓慢变化的磁场中运动时，磁矩也守恒。

粒子在随时间变化和随空间变化的磁场中运动时，磁矩都守恒。将坐标系转化为粒子导向中心的运动坐标系，当粒子沿着磁力线向磁场增强的区域运动时，粒子感受到的磁场要增强，这相当于是磁场随时间变化。因此在磁镜中运动的粒子的垂直方向的动能的变化可以认为是在粒子运动坐标系下，随时间变化的磁场激发出的电场引起的。

粒子的磁矩守恒，与粒子圆周运动的圆周所包含的磁通量守恒是等价的
$\mu=\frac{1}{2}|q| \omega_c \rho_c^2 = \frac{1}{2\pi} \frac{q^2}{m} \Phi_B$

其中 $\Phi_B$为磁通量
$\Phi_B = \pi \rho_c^2B$

如果 $\mu$为常量，那么 $\Phi_B$也为常量。