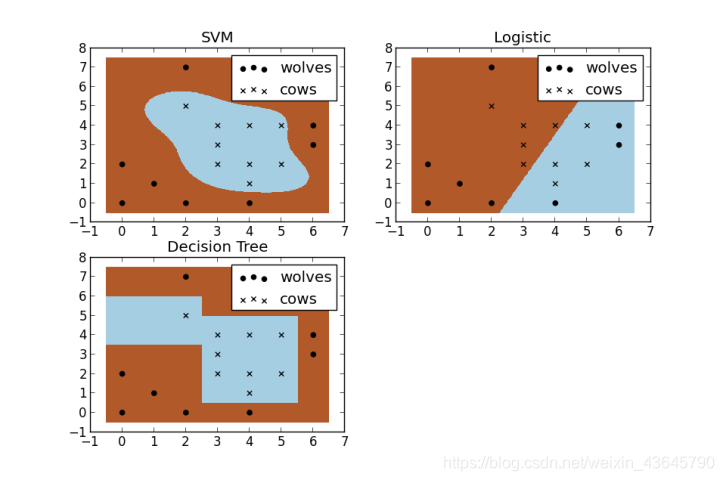
核函数
非线性问题
前面两篇文章的内容都是在样本线性可分的基础上进行的。但是现实情况却是,并不是所有的样本集都是线性可分的。对于非线性可分的数据集,如果我们仍旧采用前两篇文章的办法来进行优化求解,显然是不行的。例如:
此时我们就要寻找办法将线性不可分的样本空间转变为线性可分的样本空间。即可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。
幸运的是,如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。将线性不可分(非线性)的样本空间映射到高维空间,我们就可以利用高维特征向量进行线性分类,即将非线性问题转化为线性问题。
核函数方法

由于对于线性不可分样本空间,找到能使得样本集线性可分的高维空间很困难,且通过映射到高维特征空间,再进行内积运算,过程复杂,且不易计算,所以引入了核函数的概念:
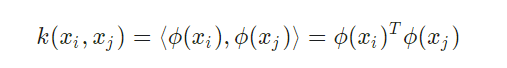
即xi和xj在特征空间的内积等于它们在原始样本空间中通过函数k(xi,xj)计算的结果,于是上面的公式可以演化为:
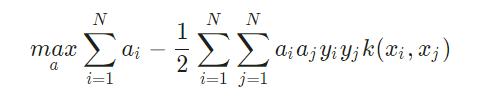
其中约束条件为:
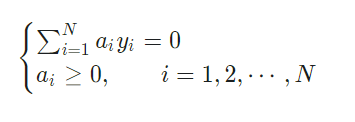
最终的决策函数模型为:
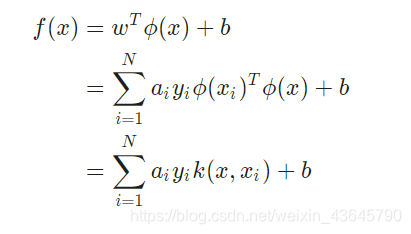
如果有一种方式可以在特征空间中直接计算内积,就像在原始输入点的函数中一样,就有可能将两个步骤融合到一起建立一个非线性的学习器,这样直接计算法的方法称为核函数方法。
通过核函数,我们就不必直接去计算高维甚至无穷维特征空间中的内积了,在原始输入空间进行计算,这大大了降低计算难度。
核函数存在条件
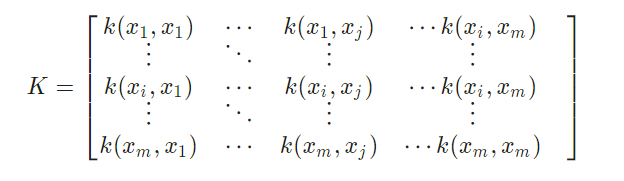
只要一个对称函数所对应的核矩阵半正定,那么它就可以作为核函数使用。事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射ϕ。换言之,任何一个核函数都隐式定义了一个称为“再生核希尔伯特空间”的特征空间。(emmm不用听懂这句话)
常见的核函数
核函数的选择要求满足Mercer定理(Mercer’s theorem),即核函数在样本空间内的任意格拉姆矩阵(Gram matrix)为半正定矩阵(semi-positive definite)。
常用的核函数有:线性核函数,多项式核函数,径向基核函数,Sigmoid核函数和复合核函数,傅立叶级数核,B样条核函数和张量积核函数等 。
下面列举几个尤其常用的核函数:
 同样,也可以通过函数组合得到核函数。
同样,也可以通过函数组合得到核函数。
核函数解决非线性问题的实例
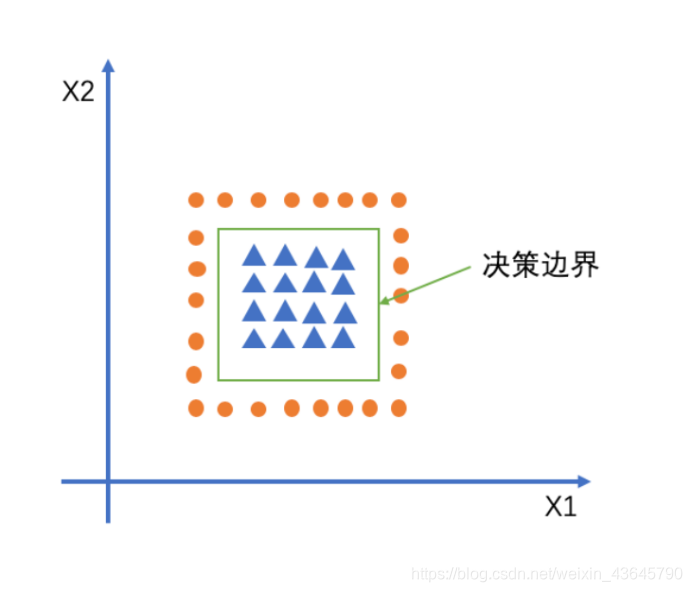
假设现在你是一个农场主,圈养了一批羊群,但为预防狼群袭击羊群,你需要搭建一个篱笆来把羊群围起来。那么篱笆应该建在哪里呢?
你很可能需要依据牛群和狼群的位置建立一个“分类器”,比较下图这几种不同的分类器,我们可以看到SVM完成了一个很完美的解决方案。