数据结构与算法之二叉搜索树

二叉搜索树

二叉搜索树又称为二叉排序树，首先二叉搜索树是一棵二叉树，所谓二叉树，就是"任意节点最多允许两个子节点"，这两个子节点称为左右子节点。

性质：

1. 若左子树非空，则左子树上的所有节点均小于其根节点
2. 若右子树非空，则右子树上的所有节点均大于其根节点

即任意节点的值一定大于其左子树中的每一个节点的值，并小于右子树中的每一个节点的值。换句话说，中序遍历二叉搜索树得到的序列为从小到大排序的有序序列。

二叉搜索树基本实现：

//二叉搜索树的实现
#include<iostream>

using namespace std;

struct Node{
    int data;//数据
    struct Node *lchild;//左孩子结点
    struct Node *rchild;//右孩子结点
    Node(int x):data(x),lchild(nullptr),rchild(nullptr){};
};
//从二叉树中搜索对应的val值，如果存在在返回该结点，若不存在则返回空指针
Node* SearchBST(Node* root,int val)
{
    while(root!=nullptr)
    {
        if(root->data == val)
            return root;
        root = root->data > val?root->lchild:root->rchild;
    }
    return nullptr;
}

//从二叉树中插入data值;root作为引用指针
void insertBST(Node* &root,int data)
{
    Node* node = new Node(data);
    //如果根结点为空
    if(root == nullptr)
    {
        root = node;
        return;
    }
    //如果当前树中已经存在相同的值的结点
    if(SearchBST(root,data)!=nullptr)
        return;
    Node* preNode = nullptr;
    Node* curNode = root;
    //寻找树中的插入位置
    while(curNode)
    {
        preNode = curNode;
        curNode = curNode->data > data?curNode->lchild:curNode->rchild;
    }
    if(preNode->data > data)
        preNode->lchild = node;
    else
        preNode->rchild = node;
}

//中序遍历树
void midOrderPrint(Node* root)
{
    if(root == nullptr)
        return;
    midOrderPrint(root->lchild);
    cout << root->data << ' ';
    midOrderPrint(root->rchild);
}
//删除树中的某个元素
void deleteBST(Node* &root,int val)
{
    if(root == nullptr)
        return;
    if(root->data == val)
    {
        Node* p = root;
        if(root->lchild == nullptr && root->rchild == nullptr)
        {
            root = nullptr;
        }else if(root->lchild == nullptr){
            root = root->rchild;
        }else if(root->rchild == nullptr){
            root = root->lchild;
        }else{
            //如果被移除节点具有两个子节点，
            //其策略是找出该节点的右子树的最小节点，并把该节点的左子树赋给最小节点
            //然后将该节点用该节点的右子树代替
            Node *temp = root->rchild;
            Node* find_out = nullptr;
            while(temp)
            {
                find_out = temp;
                temp = temp->lchild;
            }
            find_out->lchild = root->lchild;
            root = root->rchild;
        }
        delete p;
    }
    else if(root->data > val)
    {
        deleteBST(root->lchild,val);
    }
    else
    {
        deleteBST(root->rchild,val);
    }
}


int main()
{
    int num[] = {2, 1, 4, 3, 5, 6, 8, 7, 9, 10 };
    int len = sizeof(num)/sizeof(num[0]);
    Node *p = nullptr;
    for(int i = 0; i < len;i++)
    {
        insertBST(p,num[i]);
    }
    deleteBST(p,7);
    midOrderPrint(p);

    return 0;
}

注意：删除二叉搜索树中的某个元素时需要注意，删除前后应该保持二叉搜索树的条件不变。

二叉树的节点的删除

二叉树节点的删除主要包含四种情况：

1. 该节点为树的叶子，即没有左右子树
2. 该节点只有左子树，没有右子树
3. 该节点只有右子树，没有左子树
4. 该节点既有左子树又有右子树

这里前三种情况比较容易处理，这里主要讨论第四种情况。对于该节点既有左子树又有右子树，有以下两种方法：

1. 寻找该节点的右子树中值最小的节点p，然后将该节点的左子树赋给节点p，然后用该节点的右子树代替该节点即可。
2. 同样是寻找该节点右子树中值最小的节点p，然后用p的值替换该节点的值并删除p节点

以下图为例：

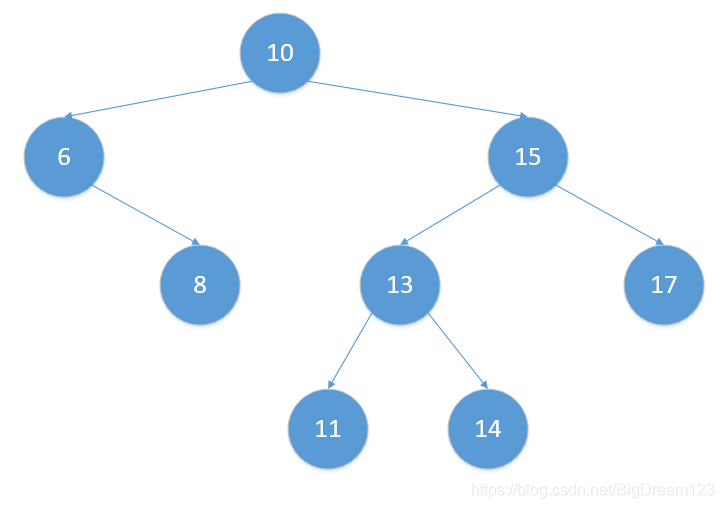
以删除节点10为例，如果利用第一种方法，则删除后的树变成：

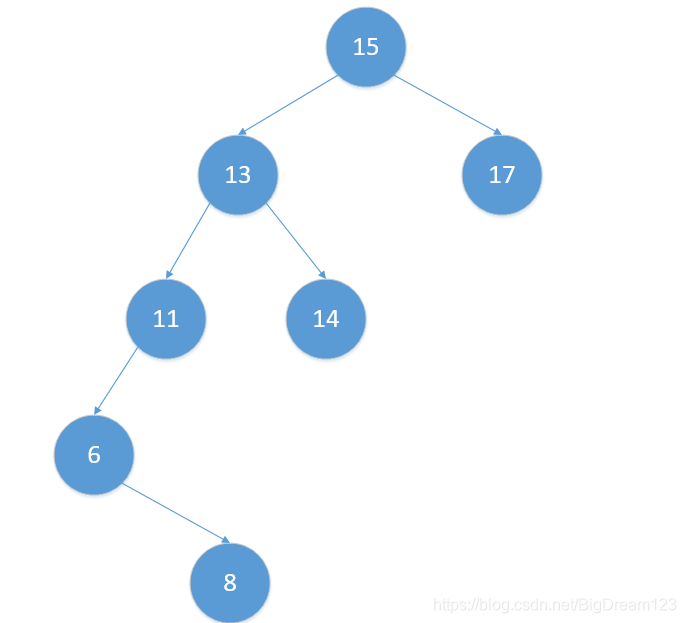
如果利用第二种方法则删除后的树变成：

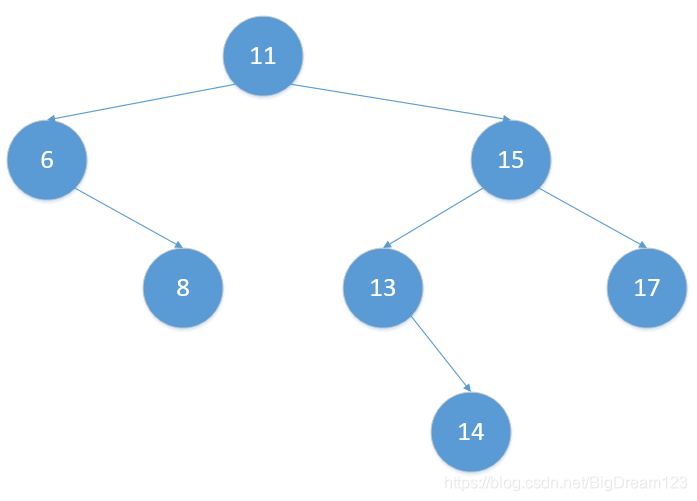
二叉搜索树的判断

构建二叉树节点的定义为：

struct Node{
    int data;//数据
    struct Node *lchild;//左孩子结点
    struct Node *rchild;//右孩子结点
};

判断一棵树是否为二叉搜索树分方法如下：

方法一（错误）

分别对于每一个节点，判断其值是否大于左子树节点，是否小于右子树节点。代码实现如下：

bool isBST(Node* root)
{
    if (root == nullptr)
        return true;
    if (root->left != NULL && root->left->data > root->data)
        return false;
    if (root->right != NULL && root->right->data < root->data)
        return false;
    //递归遍历树的左右子树
    if (!isBST(root->left) || !isBST(root->right))
        return false;
    return true;
}

但是这种方法的是错误的，它不能保证根结点的左子树和右子树的左右子树的节点满足条件。如下面例子，节点4满足上面程序但是并不满足二叉搜索的条件。

              3

            /      \

          2         5

       /     \

    1         4

方法二

对于每一个节点，检测其值是否大于左子树的最大值，是否小于右子树的最小值。思路简单，但是实现较复杂且效率低下。

int maxValue(Node *root) 
{
    int max = root->data;
    if(root->left != NULL)
    {//寻找左子树的最大值
        int maxLeft = maxValue(root->left);
        max = max > maxLeft ? max : maxLeft;
    }
    if(root->right != NULL)
    {//寻找右子树的最大值
        int maxRight = maxValue(root->right);
        max = max > maxRight ? max : maxRight;
    }
    return max;
}

int minValue(Node *root)
{
    int min = root->data;
    if(root->left != NULL)
    {//寻找左子树的最小值
        int minLeft = maxValue(root->left);
        min = min > minLeft ? min : minLeft;
    }
    if(root->right != NULL)
    {//寻找右子树的最小值
        int minRight = maxValue(root->right);
        min = min > minRight ? min : min;
    }
    return min;
}

bool isBST(Node *root)
{
    if(root == NULL)
        return true;
    if(root->left != NULL && maxValue(root->left) > root->data)
        return false;
    if(root->right != NULL && minValue(root->right) < root->data)
        return false;
    return isBST(root->left) && isBST(root->right);
}

方法三

方法三是方法二的改进，由于方法二寻找最小最大值时需要重复遍历树中的数据，如果每个数的每个节点的数据只遍历一次，则效率会提高很多。

bool isBTSMinMax(Node *root, int min, int max)
{
    if(root == NULL)
        return true;
    if(root->data < min || root->data > max)
        return false;
    return isBTSMinMax(root->left, min, root->data - 1) && isBTSMinMax(root->right, root->data + 1, max);
}

bool isBST(TreeNode *root)
{
    return isBTSMinMax(root, INT_MIN, INT_MAX);
}

这个方法的巧妙之处在于限定了子树节点的值的范围，从而每个节点只需遍历一次。

方法四

根据二叉搜索树的性质，可以检查中序遍历树所得序列是否为升序序列，如果是升序序列，则是二叉搜索树。

//中序遍历的方法实现
bool isBST(Node *root)
{
    static Node *prev;//用于保存上一次中序遍历的节点
    if(root != NULL)
    {
        if(!isBST(root->left))
            return false;
        if(prev != NULL && root->data < prev->data)
            return false;
        prev = root;
        if(!isBST(root->right))
            return false;
    }
    return true;
}

这里在中序遍历过程中，使用静态变量prev保存前驱节点，如果当前节点小于前驱节点，则该树不是二叉搜索树。