HDU 4651Partition&HDU4658(浅析整数拆分，五边形数定理）

本文用到生成函数，这里有篇我觉得讲的不错的添加链接描述
这题的意思是问一个整数可以拆分为多少种整数的相加，设数目为 $P(n)$
因为
$5=1+1+1+1+1$
$5=1+1+1+2$
$5=1+1+3$
$5=1+4$
$5=2+3$
$5=1+2+2$
$5=5$
所以 $P(5)=7$
有一些比较低效的方法，这里不说，说一种时间复杂度为 $O(n\sqrt{n})$的解法。
先说一下五边形数定理

五边形数定理

五边形数，即是如图所示，组成正五边形数的点数

这里贴一个来自百度百科的图片
第几个五边形数即是图片中对应第几张中的点数是多少
即是 $1, 5, 12, 22, 35, 51\cdots$
设 $x$个五边形数为 $K(x)$
观察图片可发现 $K(x)=K(x-1)+3*x-2$
$K(x)=1+4+7+10+13+\cdots 3*x-2=\frac{x\cdot(3x-1)}{2}$
用这公式推广到广义五角形定理。
$x$的取值是 $0,1,1,2,-2, 3,-3\cdots$
所以五边形数是
$0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92\cdots$
五边形数定理是一个由欧拉发现的数学定理，描述欧拉函数展开式的特性。–百度百科
定理描述：–百度百科

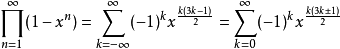
即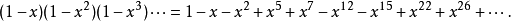
这个公式可看到指数部分即是广义五边形数，为第 $0,1-1,2,-2\cdots$个，前面系数为 $(-1)^{|m|}$ $m$表示第 $m$个五边形数
为什么是这样我也不知道，乘开后就是这样了。
那接下来描述这个定理跟我们的拆分整数有什么关系
为防止重复，我们可以这样描述一个整数n可以拆分为多少个1，多少个2，多少个3等等组成
即 $n=1*k_1+2*k_2+3*k_3+\cdots+n*k_n$
$k=0,1,\cdots$
我们把多少个1，多少个2，多少个3，搬到指数上去
所以易知
$\prod\limits _{i=1}^{\infty}\sum\limits_{j=0}^{\infty}x^{ij}= （1+x^1+x^2+x^3+\cdots）(1+x^{1*2}+x^{2*2}+x^{3*2}+\cdots)(1+x^{1*3}+x^{2*3}+x^{3*3}\cdots)\cdots=\prod\limits_{i=0}^{\infty}P(i)x^i$
这里不妨尝试这选定特定的 $i$，即 $x^i$尝试着拆一下，可以发现就是右式展开后指数相加的形式了
由生成函数 $\frac{1}{1-x}=1+x+x^2+x^3+x^4+\cdots$得
$\prod\limits_{i=0}^{\infty}P(i)x^i=\prod\limits_{i=1}^{\infty}\frac{1}{1-x^i}$这就是把五边形定理跟整数拆分结合在一起的巧妙公式了
设 $Q(x)=\prod\limits_{i=1}^{\infty}(1-x^i)$
则结合五边形数定理有
$Q(x)\prod\limits_{i=0}^{\infty}P(i)x^i=(P(0)+P(1)x+P(2)x^2+P(3)x^3+\cdots)(1-x-x^2+x^5+x^7-x^{12}\cdots)=1$
P(0)=1;
显然左边展开之后 $x^k$前的系数为0
所以 $P(k)=P(k-1)+P(k-2)-P(k-5)-P(k-7)+P(k-12)+P(k-15)$
即是广义五边形数，为第 $0,1-1,2,-2\cdots$个，前面系数为 $(-1)^{|m|+1}$
而 $K(x)=K(x-1)+3*x-2$
至持这题的整数拆分完美解决，预处理前 $n个P$时间复杂度为 $O(n\sqrt{n})$
HDU 4651代码

#include<bits/stdc++.h>
#define ll long long
#define endl '\n'
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
const int MX=4e5+7;
const int mod=1e9+7;
using namespace std;
ll qpow(ll a,ll b,ll MOD=mod){for(ll ans=1;;a=a*a%MOD,b>>=1){if(b&1)ans=ans*a%MOD;if(!b)return ans;}}
ll inv(ll a,ll MOD=mod){return qpow(a,MOD-2,MOD);}
ll __gcm(ll a,ll b){return a*b/__gcd(a,b);}
int top=0;
map<pair<int,int>,int>mp;
ll a[MX],P[MX];
int main()
{

  ios::sync_with_stdio(0),cin.tie(0);
  int t=1e5;
  for(int i=-t;i<=t;i++)
  {
      a[i+t]=1ll*i*(3*i-1)/2;
  }//存第i个五边形数
  P[1]=1,P[0]=1;
  for(int i=2;i<=t;i++)
  {
    for(int j=1;;j++)
    {
        if(a[j+t]<=i)
        {
            if(j&1)
                P[i]+=P[i-a[j+t]];
            else P[i]-=P[i-a[j+t]];//根据递归公式
        }
        if(a[t-j]<=i)
        {
            if(j&1)
            {
                P[i]+=P[i-a[t-j]];
            }
            else P[i]-=P[i-a[t-j]];
        }
        if(a[j+t]>i&&a[t-j]>i)break;
        P[i]%=mod;
        if(P[i]<0)P[i]+=mod;
    }

  }
  int T;
  cin>>T;
  while(T--)
  {
      int n;
      cin>>n;
      cout<<P[n]<<endl;
  }

}

HDU4658
这题较HDU4651多了一个限制，整数拆分后每个数的个数不能等于或多于k个，即不能有k个1，或超过k个1
设对于 $n,k$答案为 $P_k(n)$
同样构造一下有
$\prod\limits _{i=1}^{\infty}\sum\limits_{j=0}^{k-1}x^{ij}= （1+x^1+x^2+x^3+\cdots+x^{k-1}）(1+x^{1*2}+x^{2*2}+x^{3*2}+\cdots+x^{(k-1)2})(1+x^{1*3}+x^{2*3}+x^{3*3}\cdots+x^{(k-1)3})\cdots=\prod\limits_{i=0}^{\infty}P_k(i)x^i$
由等比数列前n项和易知
$\prod\limits_{i=0}^{\infty}P_k(i)x^i=\prod\limits_{i=1}^{\infty}\frac{1-x^{ki}}{1-x^i}=\frac{Q(x^{k})}{Q(x)}=Q(x^k)\prod\limits_{i=0}^{\infty}P(i)x^i$
对 $Q(x^k)$展开有 $Q(x^k)=(1-x^k-x^{2k}+x^{5k}+x^{7k}-x^{12k}\cdots)$
所以
$(P_k(0)+P_k(1)x^1+P_k(2)x^2+\cdots)=(1-x^k-x^{2k}+x^{5k}+x^{7k}-x^{12k}\cdots)(P(0)+P(1)x+P(2)x^2+P(3)x^3+\cdots)$
整理出来有
$P_k(n)=P(n)-P(n-1)-P(n-2)+P(n-5)+P(n-7)\cdots$
先预处理一下P的值，然后就可以做了
代码：

#include<bits/stdc++.h>
#define ll long long
#define endl '\n'
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
const int MX=1e6+7;
const int mod=1e9+7;
using namespace std;
ll qpow(ll a,ll b,ll MOD=mod){for(ll ans=1;;a=a*a%MOD,b>>=1){if(b&1)ans=ans*a%MOD;if(!b)return ans;}}
ll inv(ll a,ll MOD=mod){return qpow(a,MOD-2,MOD);}
ll __gcm(ll a,ll b){return a*b/__gcd(a,b);}
int top=0,t;
map<pair<int,int>,int>mp;
ll a[MX],P[MX];
void Partition()
{
  t=1e5;
  for(int i=-t;i<=t;i++)
  {
      a[i+t]=1ll*i*(3*i-1)/2;
  }
  P[1]=1,P[0]=1;
  for(int i=2;i<=t;i++)
  {
    for(int j=1;;j++)
    {
        if(a[j+t]<=i)
        {
            if(j&1)P[i]+=P[i-a[j+t]];
            else P[i]-=P[i-a[j+t]];
        }
        if(a[t-j]<=i)
        {
            if(j&1)P[i]+=P[i-a[t-j]];
            else P[i]-=P[i-a[t-j]];
        }
        if(a[j+t]>i&&a[t-j]>i)break;
        P[i]%=mod;
        if(P[i]<0)P[i]+=mod;
    }

  }
}
int main()
{

  ios::sync_with_stdio(0),cin.tie(0);
  int T;
  Partition();
  cin>>T;
  while(T--)
  {
      int n,k;
      cin>>n>>k;
      ll ans=P[n];
     for(int j=1;;j++)
    {
        if(k*a[j+t]<=n)
        {
            if(j&1)ans-=P[n-k*a[j+t]];
            else ans+=P[n-k*a[j+t]];
        }
        if(k*a[t-j]<=n)
        {
            if(j&1)ans-=P[n-k*a[t-j]];
            else ans+=P[n-k*a[t-j]];
        }
        if(a[j+t]>n&&a[t-j]>n)break;
            ans%=mod;
        if(ans<0)ans+=mod;
    }
    cout<<ans<<endl;
  }

}