如何理解非线性？用sigmoid函数画一个封闭曲线进行可视化解释

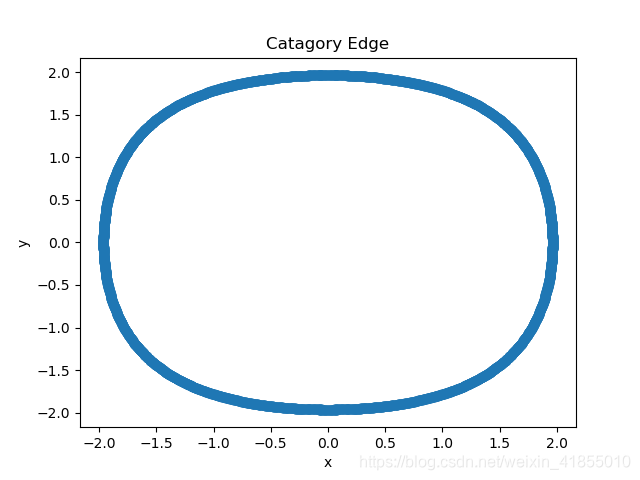
线性函数的分类的一个缺点就是只能做线性分割，因为线性函数(y=kx+b)之间无论怎么做线性组合，最后得到的还是线性函数y=kx+b，这样就不能完成类似异或问题这样的非线性分割。
那么怎么做非线性分割呢，其实中学中我们已经学过了二次曲线，二次曲线之所以能画出一个封闭的曲线，就是因为它的非线性，一方面是因为它的导数不是常数，另外一个方面，它的单调性也不是唯一的，也就是有曲线的拐点，这样就可以让曲线拐弯，最后和起点汇合形成封闭曲线。
我们观察最基本的圆方程：
x^2 + y^2=1
我们如果引入函数f(t)=t^2，稍微改写一下这个式子，就可以得到：
f(x)+f(y)=1
在这里，我们选择的函数是二次函数，如果我们把f(x)换成任意非线性函数，都可以化直为曲，换成任意具有拐点的非单调函数，都可以实现曲线的拐弯。
在这里，我们用sigmoid函数构造一个这样的类抛物线曲线。
其中，sigmoid函数的定义为：

def sigmoid(indvar):
	return 1/(1+np.exp(-indvar))

我们可以画出sigmoid函数的图像如下：

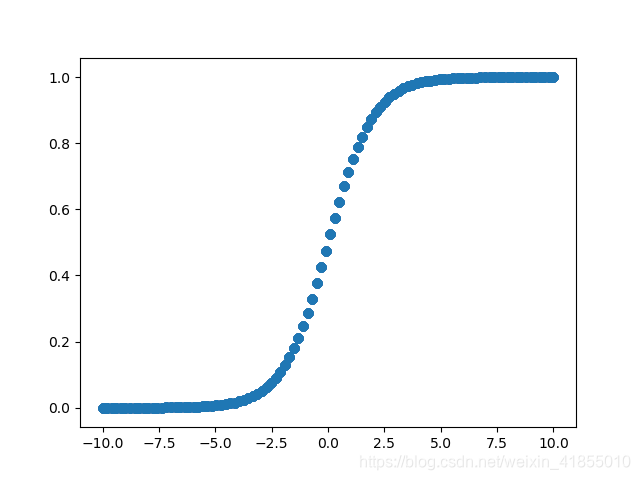
我们通过一些简单的变换，可以得到如下类抛物线曲线。

f = sigmoid(t-5)+sigmoid(-t-5)

我们可以得到一条带有拐点的微笑曲线：

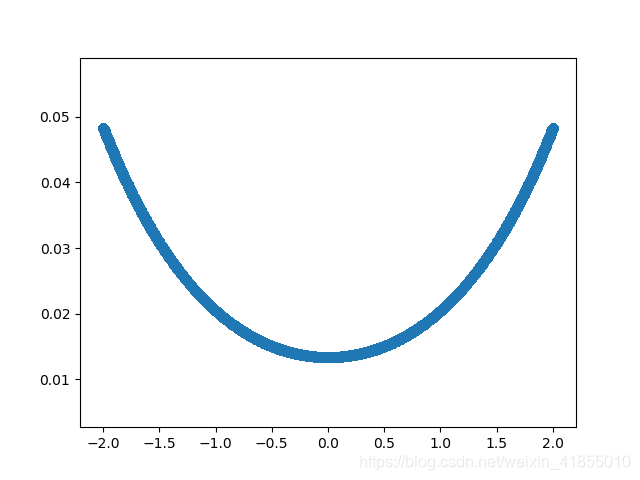
我们看到，曲线的拐点将出现在自变量取0的时候。

这样，我们就可以编写程序画出：
f(x)+f(y)=r的曲线了。
这里，我使用了自己编写的程序，这样可以控制曲线的粗细O(∩_∩)O。
完整的代码如下：

import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd
import numpy as np

def sigmoid(indvar):
	return 1/(1+np.exp(-indvar))

x = np.linspace(-2,2,1000)
y = x
x1, x2 = np.meshgrid(x, y)
o  = sigmoid(x1-5)+sigmoid(-x1-5) + sigmoid(x2-5)+sigmoid(-x2-5)
print(o)
x1 = x1.reshape(-1)
x2 = x2.reshape(-1)
o = o.reshape(-1)

data_df = pd.DataFrame({
		'x': x1,
		'y': x2,
		'z': o,
		}
	)

plt_data = data_df[data_df['z']>0.06][data_df['z']<0.0602]
plt_x = list(plt_data['x'])
plt_y = list(plt_data['y'])
plt.xlabel('x')
plt.ylabel('y')
plt.title('Catagory Edge')
plt.scatter(plt_x,plt_y)
plt.show()

运行之后，我们就可以得到如下的封闭曲线了